Zeroth-order Stochastic Compositional Algorithms for Risk-Aware Learning

We present Free-MESSAGEp, the first zeroth-order algorithm for convex mean-semideviation-based risk-aware learning, which is also the first three-level zeroth-order compositional stochastic optimization algorithm, whatsoever. Using a non-trivial extension of Nesterov's classical results on Gaussian smoothing, we develop the Free-MESSAGEp algorithm from first principles, and show that it essentially solves a smoothed surrogate to the original problem, the former being a uniform approximation of the latter, in a useful, convenient sense. We then present a complete analysis of the Free-MESSAGEp algorithm, which establishes convergence in a user-tunable neighborhood of the optimal solutions of the original problem, as well as explicit convergence rates for both convex and strongly convex costs. Orderwise, and for fixed problem parameters, our results demonstrate no sacrifice in convergence speed compared to existing first-order methods, while striking a certain balance among the condition of the problem, its dimensionality, as well as the accuracy of the obtained results, naturally extending previous results in zeroth-order risk-neutral learning.

Recursive Optimization of Convex Risk Measures: Mean-Semideviation Models

We develop recursive, data-driven, stochastic subgradient methods for optimizing a new, versatile, and application-driven class of convex risk measures, termed here as mean-semideviations, strictly generalizing the well-known and popular mean-upper-semideviation. We introduce the MESSAGEp algorithm, which is an efficient compositional subgradient procedure for iteratively solving convex mean-semideviation risk-averse problems to optimality. We analyze the asymptotic behavior of the MESSAGEp algorithm under a flexible and structure-exploiting set of problem assumptions. In particular: 1) Under appropriate stepsize rules, we establish pathwise convergence of the MESSAGEp algorithm in a strong technical sense, confirming its asymptotic consistency. 2) Assuming a strongly convex cost, we show that, for fixed semideviation order $p>1$ and for $\epsilon\in\left[0,1\right)$, the MESSAGEp algorithm achieves a squared-${\cal L}_{2}$ solution suboptimality rate of the order of ${\cal O}(n^{-\left(1-\epsilon\right)/2})$ iterations, where, for $\epsilon>0$, pathwise convergence is simultaneously guaranteed. This result establishes a rate of order arbitrarily close to ${\cal O}(n^{-1/2})$, while ensuring strongly stable pathwise operation. For $p\equiv1$, the rate order improves to ${\cal O}(n^{-2/3})$, which also suffices for pathwise convergence, and matches previous results. 3) Likewise, in the general case of a convex cost, we show that, for any $\epsilon\in\left[0,1\right)$, the MESSAGEp algorithm with iterate smoothing achieves an ${\cal L}_{1}$ objective suboptimality rate of the order of ${\cal O}(n^{-\left(1-\epsilon\right)/\left(4\bf{1}_{\left\{ p>1\right\} }+4\right)})$ iterations. This result provides maximal rates of ${\cal O}(n^{-1/4})$, if $p\equiv1$, and ${\cal O}(n^{-1/8})$, if $p>1$, matching the state of the art, as well.

Approximate Dynamic Programming for Planning a Ride-Sharing System using Autonomous Fleets of Electric Vehicles

Within a decade, almost every major auto company, along with fleet operators such as Uber, have announced plans to put autonomous vehicles on the road. At the same time, electric vehicles are quickly emerging as a next-generation technology that is cost effective, in addition to offering the benefits of reducing the carbon footprint. The combination of a centrally managed fleet of driverless vehicles, along with the operating characteristics of electric vehicles, is creating a transformative new technology that offers significant cost savings with high service levels. This problem involves a dispatch problem for assigning riders to cars, a planning problem for deciding on the fleet size, and a surge pricing problem for deciding on the price per trip. In this work, we propose to use approximate dynamic programming to develop high-quality operational dispatch strategies to determine which car (given the battery level) is best for a particular trip (considering its length and destination), when a car should be recharged, and when it should be re-positioned to a different zone which offers a higher density of trips. We then discuss surge pricing using an adaptive learning approach to decide on the price for each trip. Finally, we discuss the fleet size problem which depends on the previous two problems.

Risk-Averse Approximate Dynamic Programming with Quantile-Based Risk Measures

In this paper, we consider a finite-horizon Markov decision process (MDP) for which the objective at each stage is to minimize a quantile-based risk measure (QBRM) of the sequence of future costs; we call the overall objective a dynamic quantile-based risk measure (DQBRM). In particular, we consider optimizing dynamic risk measures where the one-step risk measures are QBRMs, a class of risk measures that includes the popular value at risk (VaR) and the conditional value at risk (CVaR). Although there is considerable theoretical development of risk-averse MDPs in the literature, the computational challenges have not been explored as thoroughly. We propose data-driven and simulation-based approximate dynamic programming (ADP) algorithms to solve the risk-averse sequential decision problem. We address the issue of inefficient sampling for risk applications in simulated settings and present a procedure, based on importance sampling, to direct samples toward the "risky region" as the ADP algorithm progresses. Finally, we show numerical results of our algorithms in the context of an application involving risk-averse bidding for energy storage.

Monte Carlo Tree Search with Sampled Information Relaxation Dual Bounds

Monte Carlo Tree Search (MCTS), most famously used in game-play artificial intelligence (e.g., the game of Go), is a well-known strategy for constructing approximate solutions to sequential decision problems. Its primary innovation is the use of a heuristic, known as a default policy, to obtain Monte Carlo estimates of downstream values for states in a decision tree. This information is used to iteratively expand the tree towards regions of states and actions that an optimal policy might visit. However, to guarantee convergence to the optimal action, MCTS requires the entire tree to be expanded asymptotically. In this paper, we propose a new technique called Primal-Dual MCTS that utilizes sampled information relaxation upper bounds on potential actions, creating the possibility of "ignoring" parts of the tree that stem from highly suboptimal choices. This allows us to prove that despite converging to a partial decision tree in the limit, the recommended action from Primal-Dual MCTS is optimal. The new approach shows significant promise when used to optimize the behavior of a single driver navigating a graph while operating on a ride-sharing platform. Numerical experiments on a real dataset of 7,000 trips in New Jersey suggest that Primal-Dual MCTS improves upon standard MCTS by producing deeper decision trees and exhibits a reduced sensitivity to the size of the action space.

Optimal Learning for Stochastic Optimization with Nonlinear Parametric Belief Models

We consider the problem of estimating the expected value of information (the knowledge gradient) for Bayesian learning problems where the belief model is nonlinear in the parameters. Our goal is to maximize some metric, while simultaneously learning the unknown parameters of the nonlinear belief model, by guiding a sequential experimentation process which is expensive. We overcome the problem of computing the expected value of an experiment, which is computationally intractable, by using a sampled approximation, which helps to guide experiments but does not provide an accurate estimate of the unknown parameters. We then introduce a resampling process which allows the sampled model to adapt to new information, exploiting past experiments. We show theoretically that the method converges asymptotically to the true parameters, while simultaneously maximizing our metric. We show empirically that the process exhibits rapid convergence, yielding good results with a very small number of experiments.

The Information-Collecting Vehicle Routing Problem: Stochastic Optimization for Emergency Storm Response

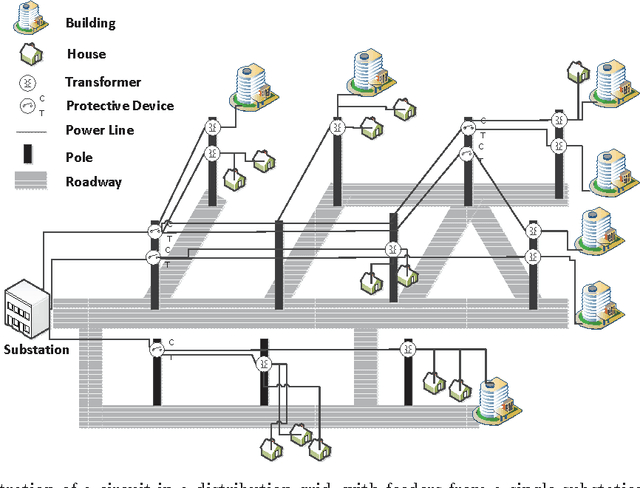
Utilities face the challenge of responding to power outages due to storms and ice damage, but most power grids are not equipped with sensors to pinpoint the precise location of the faults causing the outage. Instead, utilities have to depend primarily on phone calls (trouble calls) from customers who have lost power to guide the dispatching of utility trucks. In this paper, we develop a policy that routes a utility truck to restore outages in the power grid as quickly as possible, using phone calls to create beliefs about outages, but also using utility trucks as a mechanism for collecting additional information. This means that routing decisions change not only the physical state of the truck (as it moves from one location to another) and the grid (as the truck performs repairs), but also our belief about the network, creating the first stochastic vehicle routing problem that explicitly models information collection and belief modeling. We address the problem of managing a single utility truck, which we start by formulating as a sequential stochastic optimization model which captures our belief about the state of the grid. We propose a stochastic lookahead policy, and use Monte Carlo tree search (MCTS) to produce a practical policy that is asymptotically optimal. Simulation results show that the developed policy restores the power grid much faster compared to standard industry heuristics.

A Knowledge Gradient Policy for Sequencing Experiments to Identify the Structure of RNA Molecules Using a Sparse Additive Belief Model

We present a sparse knowledge gradient (SpKG) algorithm for adaptively selecting the targeted regions within a large RNA molecule to identify which regions are most amenable to interactions with other molecules. Experimentally, such regions can be inferred from fluorescence measurements obtained by binding a complementary probe with fluorescence markers to the targeted regions. We use a biophysical model which shows that the fluorescence ratio under the log scale has a sparse linear relationship with the coefficients describing the accessibility of each nucleotide, since not all sites are accessible (due to the folding of the molecule). The SpKG algorithm uniquely combines the Bayesian ranking and selection problem with the frequentist $\ell_1$ regularized regression approach Lasso. We use this algorithm to identify the sparsity pattern of the linear model as well as sequentially decide the best regions to test before experimental budget is exhausted. Besides, we also develop two other new algorithms: batch SpKG algorithm, which generates more suggestions sequentially to run parallel experiments; and batch SpKG with a procedure which we call length mutagenesis. It dynamically adds in new alternatives, in the form of types of probes, are created by inserting, deleting or mutating nucleotides within existing probes. In simulation, we demonstrate these algorithms on the Group I intron (a mid-size RNA molecule), showing that they efficiently learn the correct sparsity pattern, identify the most accessible region, and outperform several other policies.

A New Optimal Stepsize For Approximate Dynamic Programming

Approximate dynamic programming (ADP) has proven itself in a wide range of applications spanning large-scale transportation problems, health care, revenue management, and energy systems. The design of effective ADP algorithms has many dimensions, but one crucial factor is the stepsize rule used to update a value function approximation. Many operations research applications are computationally intensive, and it is important to obtain good results quickly. Furthermore, the most popular stepsize formulas use tunable parameters and can produce very poor results if tuned improperly. We derive a new stepsize rule that optimizes the prediction error in order to improve the short-term performance of an ADP algorithm. With only one, relatively insensitive tunable parameter, the new rule adapts to the level of noise in the problem and produces faster convergence in numerical experiments.

Least Squares Policy Iteration with Instrumental Variables vs. Direct Policy Search: Comparison Against Optimal Benchmarks Using Energy Storage

This paper studies approximate policy iteration (API) methods which use least-squares Bellman error minimization for policy evaluation. We address several of its enhancements, namely, Bellman error minimization using instrumental variables, least-squares projected Bellman error minimization, and projected Bellman error minimization using instrumental variables. We prove that for a general discrete-time stochastic control problem, Bellman error minimization using instrumental variables is equivalent to both variants of projected Bellman error minimization. An alternative to these API methods is direct policy search based on knowledge gradient. The practical performance of these three approximate dynamic programming methods are then investigated in the context of an application in energy storage, integrated with an intermittent wind energy supply to fully serve a stochastic time-varying electricity demand. We create a library of test problems using real-world data and apply value iteration to find their optimal policies. These benchmarks are then used to compare the developed policies. Our analysis indicates that API with instrumental variables Bellman error minimization prominently outperforms API with least-squares Bellman error minimization. However, these approaches underperform our direct policy search implementation.