Pessimistic asynchronous sampling in high-cost Bayesian optimization

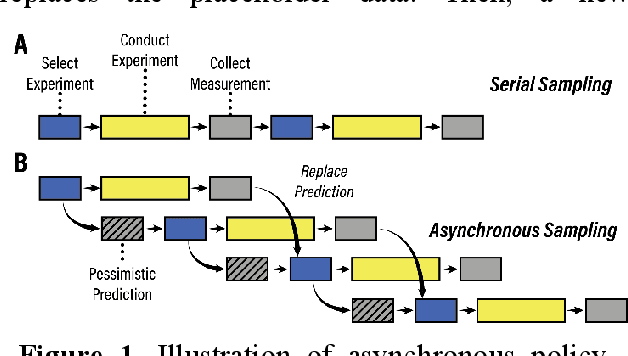
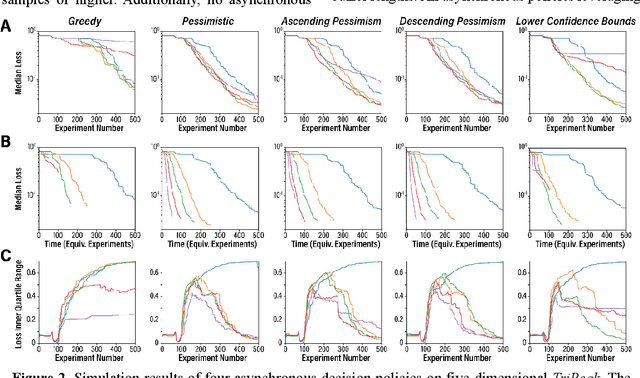
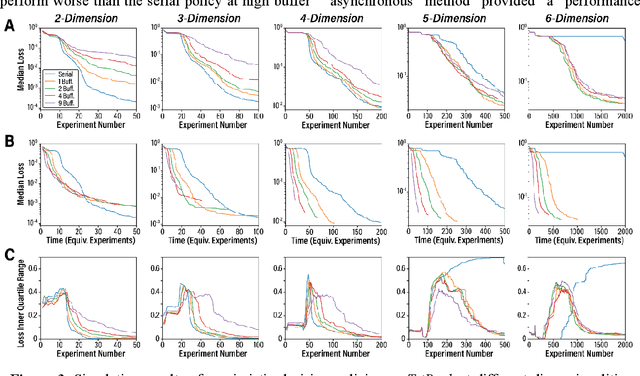
Asynchronous Bayesian optimization is a recently implemented technique that allows for parallel operation of experimental systems and disjointed workflows. Contrasting with serial Bayesian optimization which individually selects experiments one at a time after conducting a measurement for each experiment, asynchronous policies sequentially assign multiple experiments before measurements can be taken and evaluate new measurements continuously as they are made available. This technique allows for faster data generation and therefore faster optimization of an experimental space. This work extends the capabilities of asynchronous optimization methods beyond prior studies by evaluating four additional policies that incorporate pessimistic predictions in the training data set. Combined with a conventional greedy policy, the five total policies were evaluated in a simulated environment and benchmarked with serial sampling. Under some conditions and parameter space dimensionalities, the pessimistic asynchronous policy reached optimum experimental conditions in significantly fewer experiments than equivalent serial policies and proved to be less susceptible to convergence onto local optima at higher dimensions. Without accounting for the faster sampling rate, the pessimistic asynchronous algorithm presented in this work could result in more efficient algorithm driven optimization of high-cost experimental spaces. Accounting for sampling rate, the presented asynchronous algorithm could allow for faster optimization in experimental spaces where multiple experiments can be run before results are collected.

A Rigorous Uncertainty-Aware Quantification Framework Is Essential for Reproducible and Replicable Machine Learning Workflows

The ability to replicate predictions by machine learning (ML) or artificial intelligence (AI) models and results in scientific workflows that incorporate such ML/AI predictions is driven by numerous factors. An uncertainty-aware metric that can quantitatively assess the reproducibility of quantities of interest (QoI) would contribute to the trustworthiness of results obtained from scientific workflows involving ML/AI models. In this article, we discuss how uncertainty quantification (UQ) in a Bayesian paradigm can provide a general and rigorous framework for quantifying reproducibility for complex scientific workflows. Such as framework has the potential to fill a critical gap that currently exists in ML/AI for scientific workflows, as it will enable researchers to determine the impact of ML/AI model prediction variability on the predictive outcomes of ML/AI-powered workflows. We expect that the envisioned framework will contribute to the design of more reproducible and trustworthy workflows for diverse scientific applications, and ultimately, accelerate scientific discoveries.

Exact Gaussian Processes for Massive Datasets via Non-Stationary Sparsity-Discovering Kernels

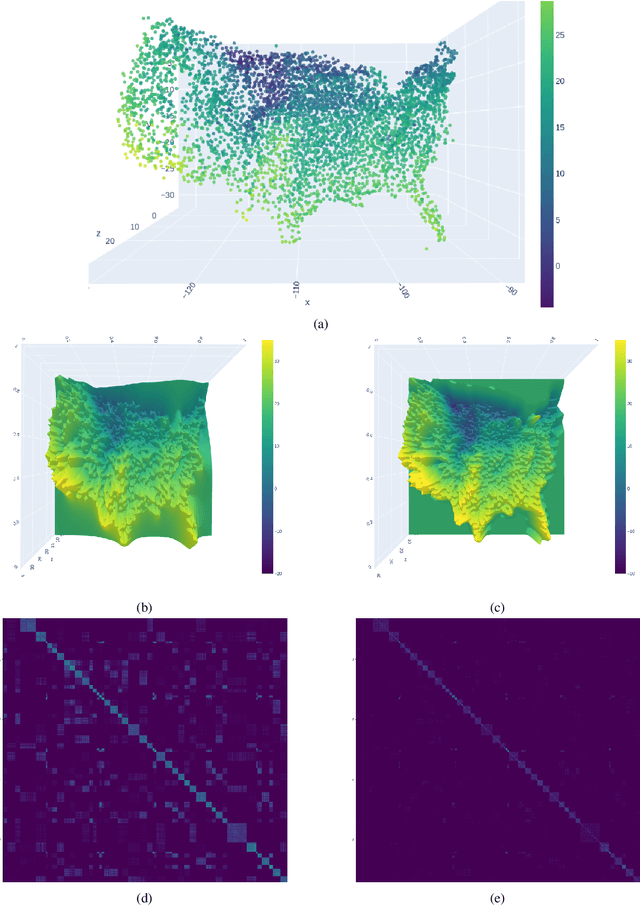
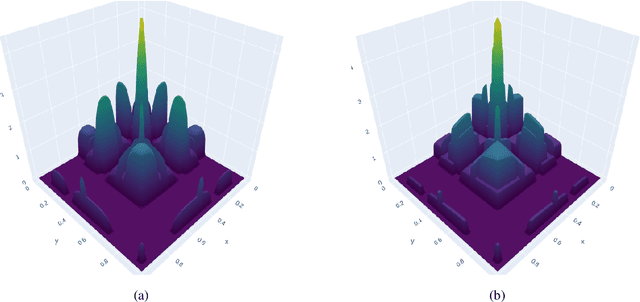
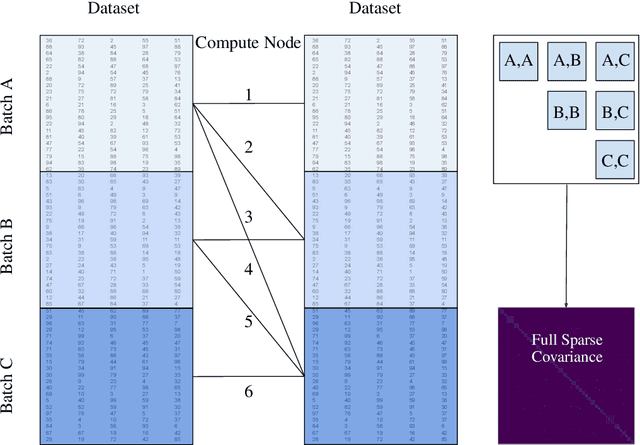
A Gaussian Process (GP) is a prominent mathematical framework for stochastic function approximation in science and engineering applications. This success is largely attributed to the GP's analytical tractability, robustness, non-parametric structure, and natural inclusion of uncertainty quantification. Unfortunately, the use of exact GPs is prohibitively expensive for large datasets due to their unfavorable numerical complexity of $O(N^3)$ in computation and $O(N^2)$ in storage. All existing methods addressing this issue utilize some form of approximation -- usually considering subsets of the full dataset or finding representative pseudo-points that render the covariance matrix well-structured and sparse. These approximate methods can lead to inaccuracies in function approximations and often limit the user's flexibility in designing expressive kernels. Instead of inducing sparsity via data-point geometry and structure, we propose to take advantage of naturally-occurring sparsity by allowing the kernel to discover -- instead of induce -- sparse structure. The premise of this paper is that GPs, in their most native form, are often naturally sparse, but commonly-used kernels do not allow us to exploit this sparsity. The core concept of exact, and at the same time sparse GPs relies on kernel definitions that provide enough flexibility to learn and encode not only non-zero but also zero covariances. This principle of ultra-flexible, compactly-supported, and non-stationary kernels, combined with HPC and constrained optimization, lets us scale exact GPs well beyond 5 million data points.

Problem-fluent models for complex decision-making in autonomous materials research

We review our recent work in the area of autonomous materials research, highlighting the coupling of machine learning methods and models and more problem-aware modeling. We review the general Bayesian framework for closed-loop design employed by many autonomous materials platforms. We then provide examples of our work on such platforms. We finally review our approaches to extend current statistical and ML models to better reflect problem-specific structure including the use of physics-based models and incorporation of operational considerations into the decision-making procedure.

A Knowledge Gradient Policy for Sequencing Experiments to Identify the Structure of RNA Molecules Using a Sparse Additive Belief Model

We present a sparse knowledge gradient (SpKG) algorithm for adaptively selecting the targeted regions within a large RNA molecule to identify which regions are most amenable to interactions with other molecules. Experimentally, such regions can be inferred from fluorescence measurements obtained by binding a complementary probe with fluorescence markers to the targeted regions. We use a biophysical model which shows that the fluorescence ratio under the log scale has a sparse linear relationship with the coefficients describing the accessibility of each nucleotide, since not all sites are accessible (due to the folding of the molecule). The SpKG algorithm uniquely combines the Bayesian ranking and selection problem with the frequentist $\ell_1$ regularized regression approach Lasso. We use this algorithm to identify the sparsity pattern of the linear model as well as sequentially decide the best regions to test before experimental budget is exhausted. Besides, we also develop two other new algorithms: batch SpKG algorithm, which generates more suggestions sequentially to run parallel experiments; and batch SpKG with a procedure which we call length mutagenesis. It dynamically adds in new alternatives, in the form of types of probes, are created by inserting, deleting or mutating nucleotides within existing probes. In simulation, we demonstrate these algorithms on the Group I intron (a mid-size RNA molecule), showing that they efficiently learn the correct sparsity pattern, identify the most accessible region, and outperform several other policies.