Modeling Multi-Step Scientific Processes with Graph Transformer Networks

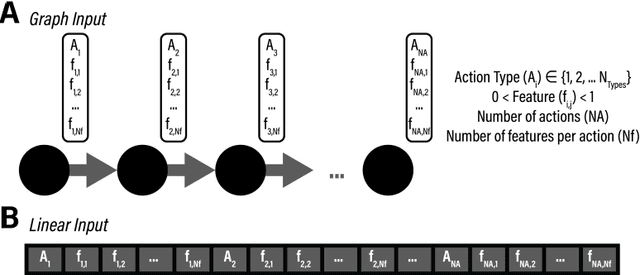
This work presents the use of graph learning for the prediction of multi-step experimental outcomes for applications across experimental research, including material science, chemistry, and biology. The viability of geometric learning for regression tasks was benchmarked against a collection of linear models through a combination of simulated and real-world data training studies. First, a selection of five arbitrarily designed multi-step surrogate functions were developed to reflect various features commonly found within experimental processes. A graph transformer network outperformed all tested linear models in scenarios that featured hidden interactions between process steps and sequence dependent features, while retaining equivalent performance in sequence agnostic scenarios. Then, a similar comparison was applied to real-world literature data on algorithm guided colloidal atomic layer deposition. Using the complete reaction sequence as training data, the graph neural network outperformed all linear models in predicting the three spectral properties for most training set sizes. Further implementation of graph neural networks and geometric representation of scientific processes for the prediction of experiment outcomes could lead to algorithm driven navigation of higher dimension parameter spaces and efficient exploration of more dynamic systems.

Pessimistic asynchronous sampling in high-cost Bayesian optimization

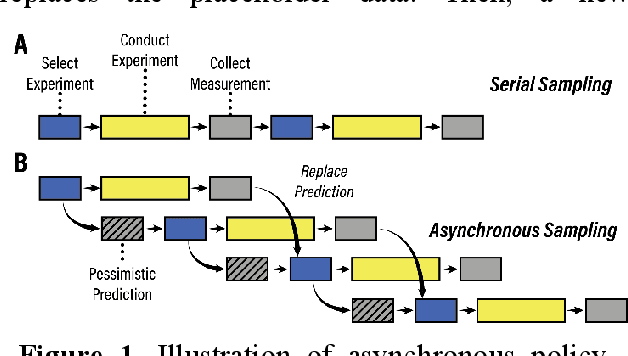
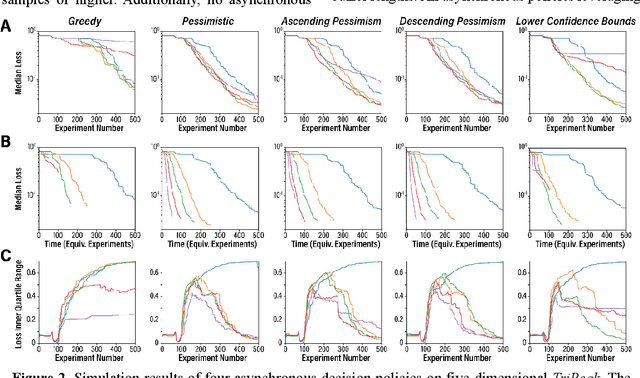
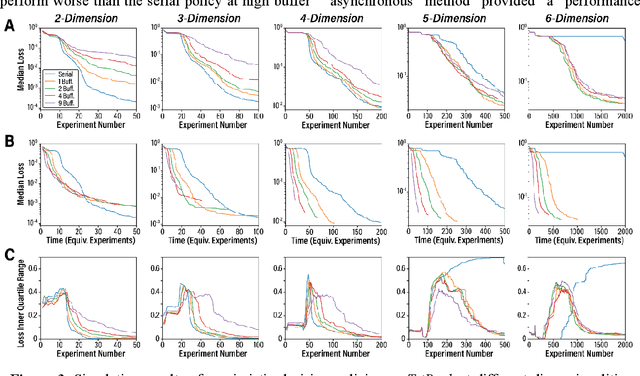
Asynchronous Bayesian optimization is a recently implemented technique that allows for parallel operation of experimental systems and disjointed workflows. Contrasting with serial Bayesian optimization which individually selects experiments one at a time after conducting a measurement for each experiment, asynchronous policies sequentially assign multiple experiments before measurements can be taken and evaluate new measurements continuously as they are made available. This technique allows for faster data generation and therefore faster optimization of an experimental space. This work extends the capabilities of asynchronous optimization methods beyond prior studies by evaluating four additional policies that incorporate pessimistic predictions in the training data set. Combined with a conventional greedy policy, the five total policies were evaluated in a simulated environment and benchmarked with serial sampling. Under some conditions and parameter space dimensionalities, the pessimistic asynchronous policy reached optimum experimental conditions in significantly fewer experiments than equivalent serial policies and proved to be less susceptible to convergence onto local optima at higher dimensions. Without accounting for the faster sampling rate, the pessimistic asynchronous algorithm presented in this work could result in more efficient algorithm driven optimization of high-cost experimental spaces. Accounting for sampling rate, the presented asynchronous algorithm could allow for faster optimization in experimental spaces where multiple experiments can be run before results are collected.