Reward Shaping for User Satisfaction in a REINFORCE Recommender

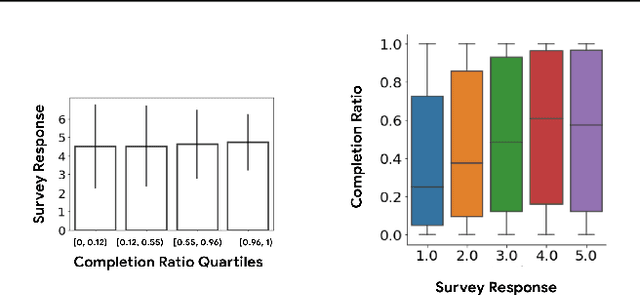
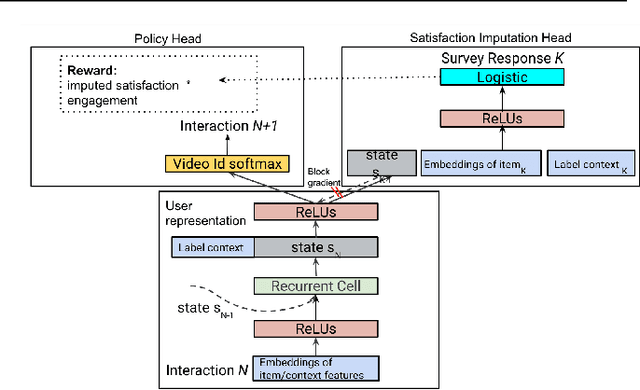
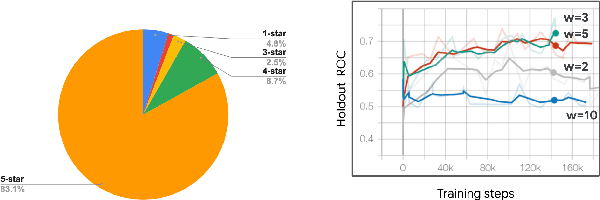
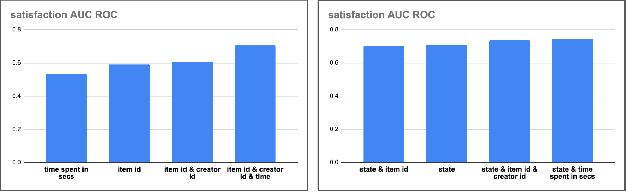
How might we design Reinforcement Learning (RL)-based recommenders that encourage aligning user trajectories with the underlying user satisfaction? Three research questions are key: (1) measuring user satisfaction, (2) combatting sparsity of satisfaction signals, and (3) adapting the training of the recommender agent to maximize satisfaction. For measurement, it has been found that surveys explicitly asking users to rate their experience with consumed items can provide valuable orthogonal information to the engagement/interaction data, acting as a proxy to the underlying user satisfaction. For sparsity, i.e, only being able to observe how satisfied users are with a tiny fraction of user-item interactions, imputation models can be useful in predicting satisfaction level for all items users have consumed. For learning satisfying recommender policies, we postulate that reward shaping in RL recommender agents is powerful for driving satisfying user experiences. Putting everything together, we propose to jointly learn a policy network and a satisfaction imputation network: The role of the imputation network is to learn which actions are satisfying to the user; while the policy network, built on top of REINFORCE, decides which items to recommend, with the reward utilizing the imputed satisfaction. We use both offline analysis and live experiments in an industrial large-scale recommendation platform to demonstrate the promise of our approach for satisfying user experiences.

Measuring Model Fairness under Noisy Covariates: A Theoretical Perspective

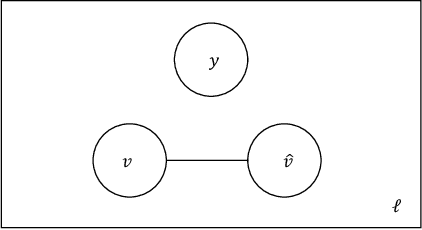
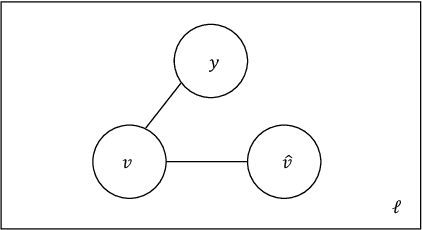
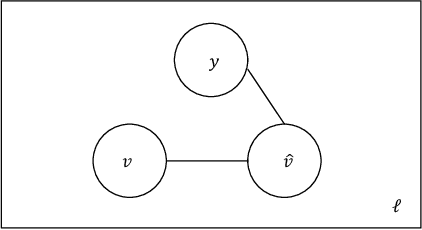
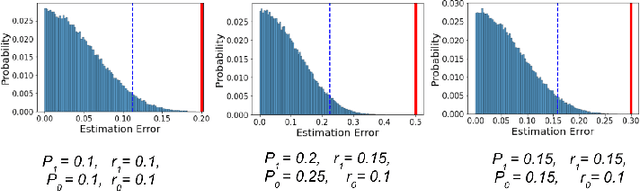
In this work we study the problem of measuring the fairness of a machine learning model under noisy information. Focusing on group fairness metrics, we investigate the particular but common situation when the evaluation requires controlling for the confounding effect of covariate variables. In a practical setting, we might not be able to jointly observe the covariate and group information, and a standard workaround is to then use proxies for one or more of these variables. Prior works have demonstrated the challenges with using a proxy for sensitive attributes, and strong independence assumptions are needed to provide guarantees on the accuracy of the noisy estimates. In contrast, in this work we study using a proxy for the covariate variable and present a theoretical analysis that aims to characterize weaker conditions under which accurate fairness evaluation is possible. Furthermore, our theory identifies potential sources of errors and decouples them into two interpretable parts $\gamma$ and $\epsilon$. The first part $\gamma$ depends solely on the performance of the proxy such as precision and recall, whereas the second part $\epsilon$ captures correlations between all the variables of interest. We show that in many scenarios the error in the estimates is dominated by $\gamma$ via a linear dependence, whereas the dependence on the correlations $\epsilon$ only constitutes a lower order term. As a result we expand the understanding of scenarios where measuring model fairness via proxies can be an effective approach. Finally, we compare, via simulations, the theoretical upper-bounds to the distribution of simulated estimation errors and show that assuming some structure on the data, even weak, is key to significantly improve both theoretical guarantees and empirical results.