Unshackling Context Length: An Efficient Selective Attention Approach through Query-Key Compression

Handling long-context sequences efficiently remains a significant challenge in large language models (LLMs). Existing methods for token selection in sequence extrapolation either employ a permanent eviction strategy or select tokens by chunk, which may lead to the loss of critical information. We propose Efficient Selective Attention (ESA), a novel approach that extends context length by efficiently selecting the most critical tokens at the token level to compute attention. ESA reduces the computational complexity of token selection by compressing query and key vectors into lower-dimensional representations. We evaluate ESA on long sequence benchmarks with maximum lengths up to 256k using open-source LLMs with context lengths of 8k and 32k. ESA outperforms other selective attention methods, especially in tasks requiring the retrieval of multiple pieces of information, achieving comparable performance to full-attention extrapolation methods across various tasks, with superior results in certain tasks.

Scalable Variational Bayesian Kernel Selection for Sparse Gaussian Process Regression

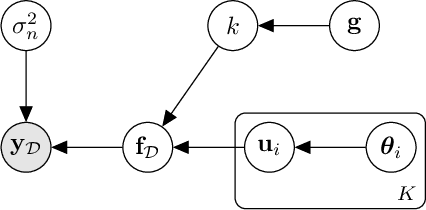
This paper presents a variational Bayesian kernel selection (VBKS) algorithm for sparse Gaussian process regression (SGPR) models. In contrast to existing GP kernel selection algorithms that aim to select only one kernel with the highest model evidence, our proposed VBKS algorithm considers the kernel as a random variable and learns its belief from data such that the uncertainty of the kernel can be interpreted and exploited to avoid overconfident GP predictions. To achieve this, we represent the probabilistic kernel as an additional variational variable in a variational inference (VI) framework for SGPR models where its posterior belief is learned together with that of the other variational variables (i.e., inducing variables and kernel hyperparameters). In particular, we transform the discrete kernel belief into a continuous parametric distribution via reparameterization in order to apply VI. Though it is computationally challenging to jointly optimize a large number of hyperparameters due to many kernels being evaluated simultaneously by our VBKS algorithm, we show that the variational lower bound of the log-marginal likelihood can be decomposed into an additive form such that each additive term depends only on a disjoint subset of the variational variables and can thus be optimized independently. Stochastic optimization is then used to maximize the variational lower bound by iteratively improving the variational approximation of the exact posterior belief via stochastic gradient ascent, which incurs constant time per iteration and hence scales to big data. We empirically evaluate the performance of our VBKS algorithm on synthetic and massive real-world datasets.