Robust A-Optimal Experimental Design for Bayesian Inverse Problems

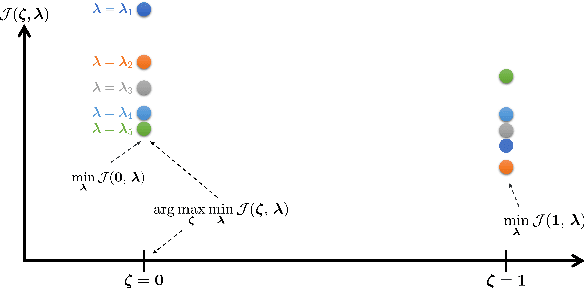
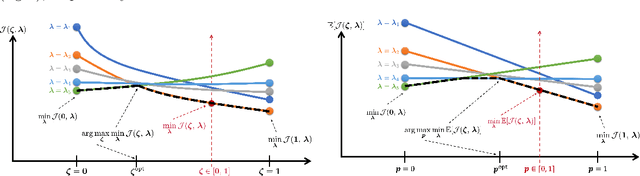
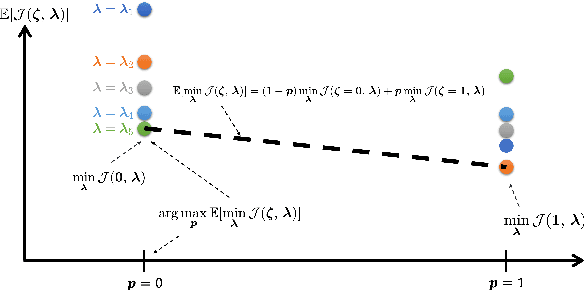
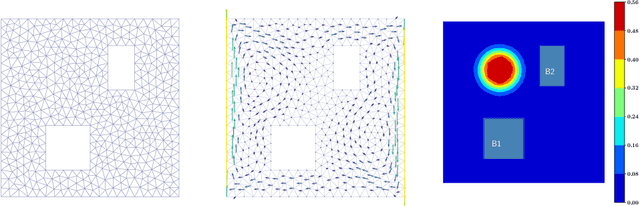
Optimal design of experiments for Bayesian inverse problems has recently gained wide popularity and attracted much attention, especially in the computational science and Bayesian inversion communities. An optimal design maximizes a predefined utility function that is formulated in terms of the elements of an inverse problem, an example being optimal sensor placement for parameter identification. The state-of-the-art algorithmic approaches following this simple formulation generally overlook misspecification of the elements of the inverse problem, such as the prior or the measurement uncertainties. This work presents an efficient algorithmic approach for designing optimal experimental design schemes for Bayesian inverse problems such that the optimal design is robust to misspecification of elements of the inverse problem. Specifically, we consider a worst-case scenario approach for the uncertain or misspecified parameters, formulate robust objectives, and propose an algorithmic approach for optimizing such objectives. Both relaxation and stochastic solution approaches are discussed with detailed analysis and insight into the interpretation of the problem and the proposed algorithmic approach. Extensive numerical experiments to validate and analyze the proposed approach are carried out for sensor placement in a parameter identification problem.

Achieving 100X faster simulations of complex biological phenomena by coupling ML to HPC ensembles

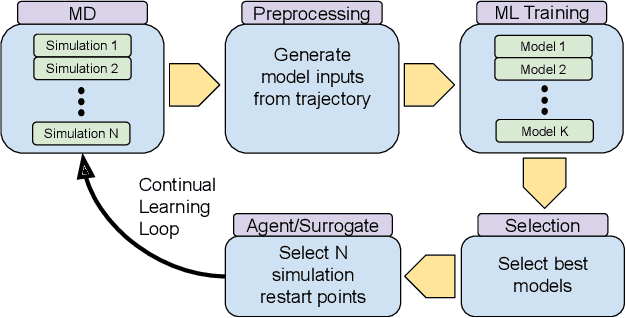
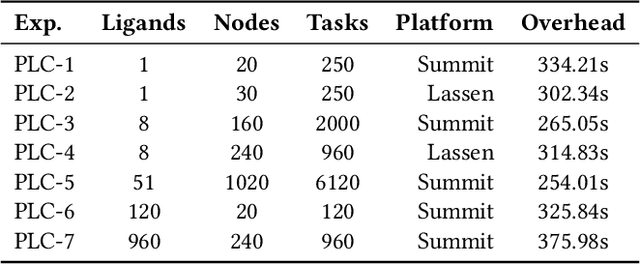
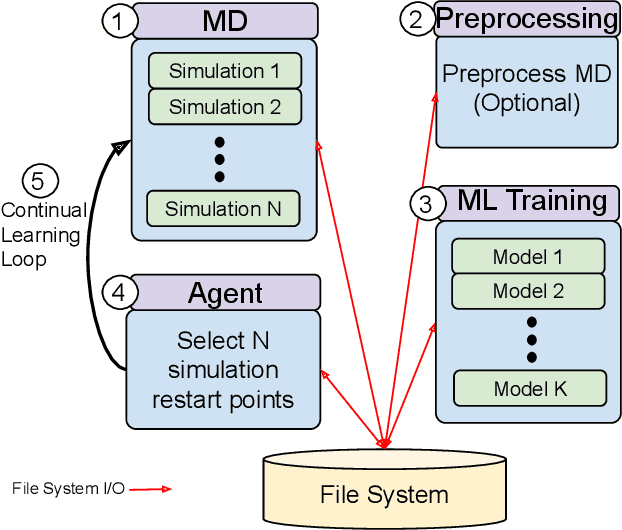
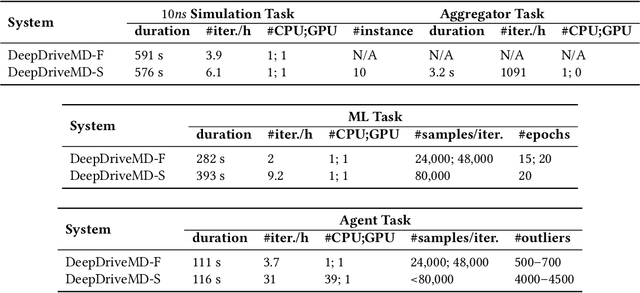
The use of ML methods to dynamically steer ensemble-based simulations promises significant improvements in the performance of scientific applications. We present DeepDriveMD, a tool for a range of prototypical ML-driven HPC simulation scenarios, and use it to quantify improvements in the scientific performance of ML-driven ensemble-based applications. We discuss its design and characterize its performance. Motivated by the potential for further scientific improvements and applicability to more sophisticated physical systems, we extend the design of DeepDriveMD to support stream-based communication between simulations and learning methods. It demonstrates a 100x speedup to fold proteins, and performs 1.6x more simulations per unit time, improving resource utilization compared to the sequential framework. Experiments are performed on leadership-class platforms, at scales of up to O(1000) nodes, and for production workloads. We establish DeepDriveMD as a high-performance framework for ML-driven HPC simulation scenarios, that supports diverse simulation and ML back-ends, and which enables new scientific insights by improving length- and time-scale accessed.

Stochastic Learning Approach to Binary Optimization for Optimal Design of Experiments

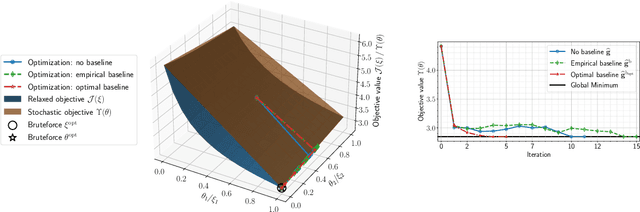
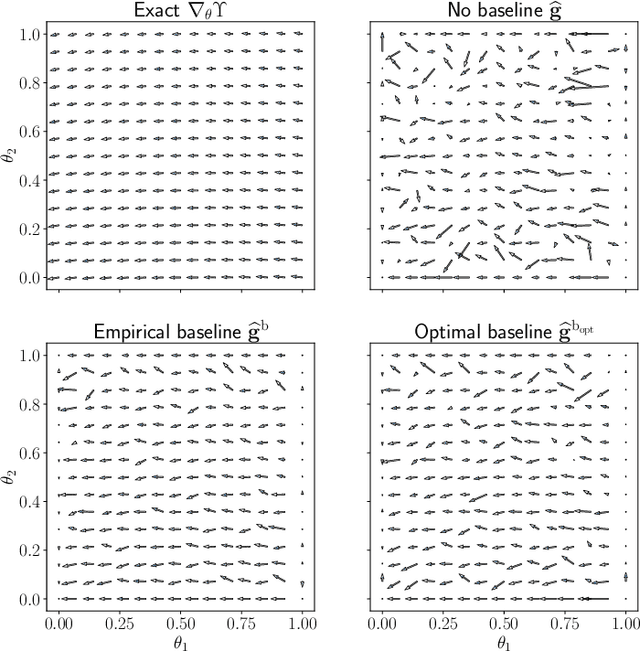
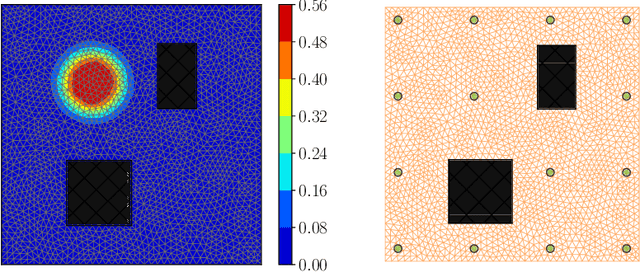
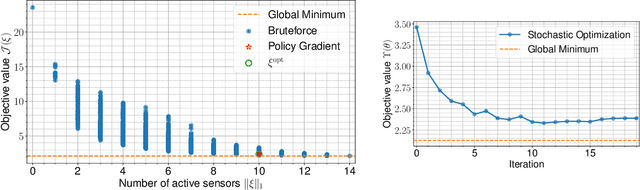
We present a novel stochastic approach to binary optimization for optimal experimental design (OED) for Bayesian inverse problems governed by mathematical models such as partial differential equations. The OED utility function, namely, the regularized optimality criterion, is cast into a stochastic objective function in the form of an expectation over a multivariate Bernoulli distribution. The probabilistic objective is then solved by using a stochastic optimization routine to find an optimal observational policy. The proposed approach is analyzed from an optimization perspective and also from a machine learning perspective with correspondence to policy gradient reinforcement learning. The approach is demonstrated numerically by using an idealized two-dimensional Bayesian linear inverse problem, and validated by extensive numerical experiments carried out for sensor placement in a parameter identification setup.

Training neural networks under physical constraints using a stochastic augmented Lagrangian approach

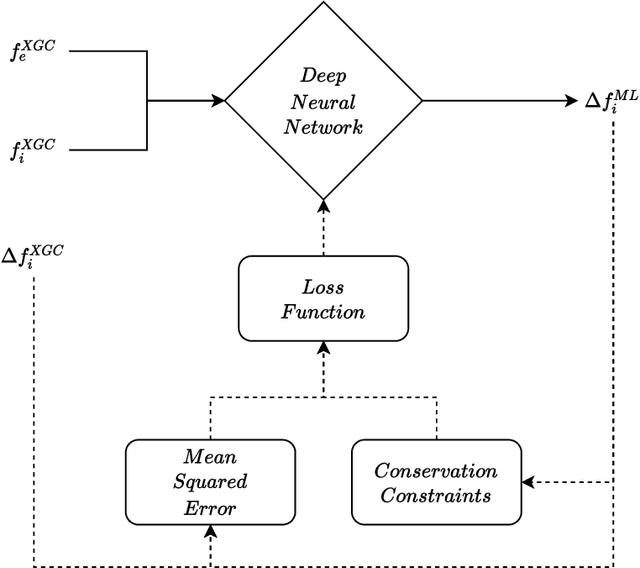
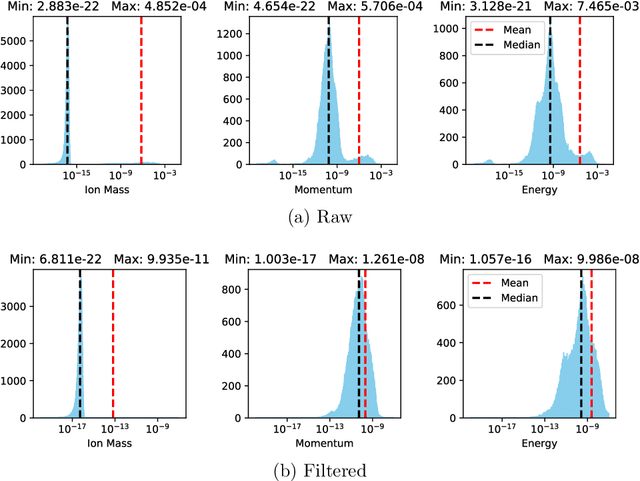
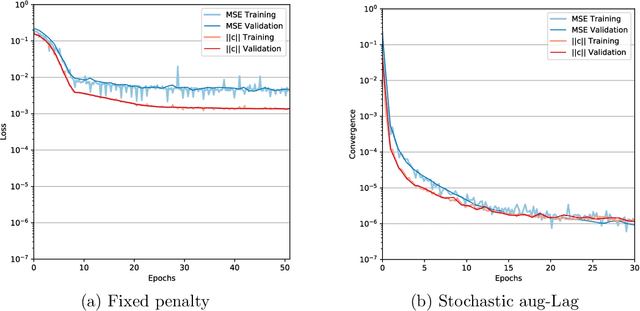
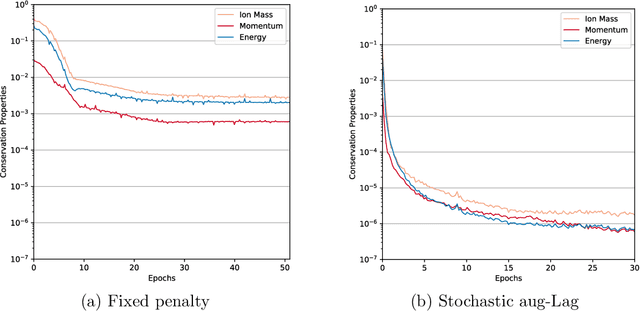
We investigate the physics-constrained training of an encoder-decoder neural network for approximating the Fokker-Planck-Landau collision operator in the 5-dimensional kinetic fusion simulation in XGC. To train this network, we propose a stochastic augmented Lagrangian approach that utilizes pyTorch's native stochastic gradient descent method to solve the inner unconstrained minimization subproblem, paired with a heuristic update for the penalty factor and Lagrange multipliers in the outer augmented Lagrangian loop. Our training results for a single ion species case, with self-collisions and collision against electrons, show that the proposed stochastic augmented Lagrangian approach can achieve higher model prediction accuracy than training with a fixed penalty method for our application problem, with the accuracy high enough for practical applications in kinetic simulations.