Multi-Stage Speaker Diarization for Noisy Classrooms

Speaker diarization, the process of identifying "who spoke when" in audio recordings, is essential for understanding classroom dynamics. However, classroom settings present distinct challenges, including poor recording quality, high levels of background noise, overlapping speech, and the difficulty of accurately capturing children's voices. This study investigates the effectiveness of multi-stage diarization models using Nvidia's NeMo diarization pipeline. We assess the impact of denoising on diarization accuracy and compare various voice activity detection (VAD) models, including self-supervised transformer-based frame-wise VAD models. We also explore a hybrid VAD approach that integrates Automatic Speech Recognition (ASR) word-level timestamps with frame-level VAD predictions. We conduct experiments using two datasets from English speaking classrooms to separate teacher vs. student speech and to separate all speakers. Our results show that denoising significantly improves the Diarization Error Rate (DER) by reducing the rate of missed speech. Additionally, training on both denoised and noisy datasets leads to substantial performance gains in noisy conditions. The hybrid VAD model leads to further improvements in speech detection, achieving a DER as low as 17% in teacher-student experiments and 45% in all-speaker experiments. However, we also identified trade-offs between voice activity detection and speaker confusion. Overall, our study highlights the effectiveness of multi-stage diarization models and integrating ASR-based information for enhancing speaker diarization in noisy classroom environments.

Probabilistic Approach to Black-Box Binary Optimization with Budget Constraints: Application to Sensor Placement

We present a fully probabilistic approach for solving binary optimization problems with black-box objective functions and with budget constraints. In the probabilistic approach, the optimization variable is viewed as a random variable and is associated with a parametric probability distribution. The original optimization problem is replaced with an optimization over the expected value of the original objective, which is then optimized over the probability distribution parameters. The resulting optimal parameter (optimal policy) is used to sample the binary space to produce estimates of the optimal solution(s) of the original binary optimization problem. The probability distribution is chosen from the family of Bernoulli models because the optimization variable is binary. The optimization constraints generally restrict the feasibility region. This can be achieved by modeling the random variable with a conditional distribution given satisfiability of the constraints. Thus, in this work we develop conditional Bernoulli distributions to model the random variable conditioned by the total number of nonzero entries, that is, the budget constraint. This approach (a) is generally applicable to binary optimization problems with nonstochastic black-box objective functions and budget constraints; (b) accounts for budget constraints by employing conditional probabilities that sample only the feasible region and thus considerably reduces the computational cost compared with employing soft constraints; and (c) does not employ soft constraints and thus does not require tuning of a regularization parameter, for example to promote sparsity, which is challenging in sensor placement optimization problems. The proposed approach is verified numerically by using an idealized bilinear binary optimization problem and is validated by using a sensor placement experiment in a parameter identification setup.

Robust A-Optimal Experimental Design for Bayesian Inverse Problems

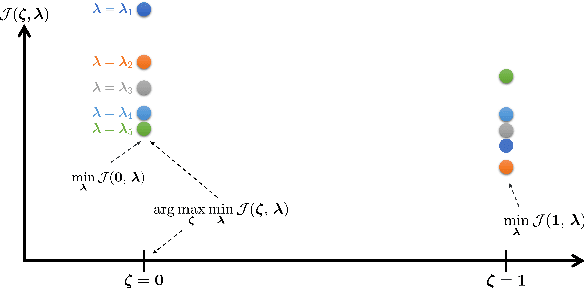
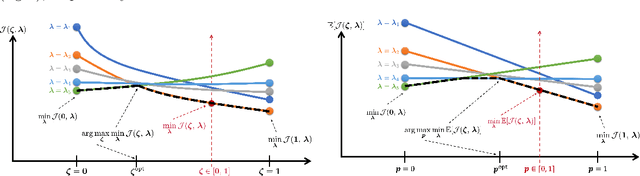
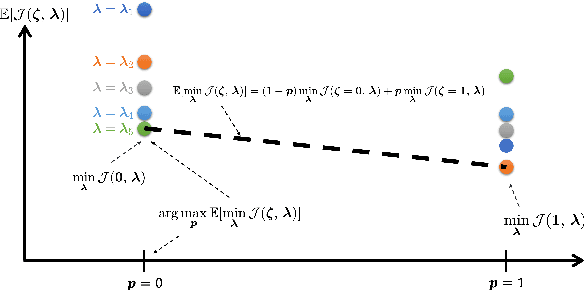
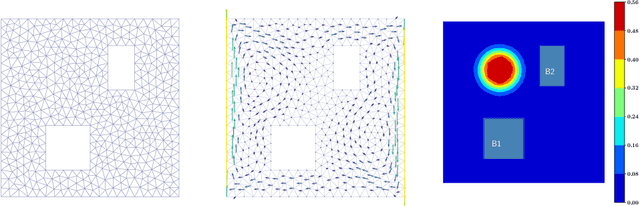
Optimal design of experiments for Bayesian inverse problems has recently gained wide popularity and attracted much attention, especially in the computational science and Bayesian inversion communities. An optimal design maximizes a predefined utility function that is formulated in terms of the elements of an inverse problem, an example being optimal sensor placement for parameter identification. The state-of-the-art algorithmic approaches following this simple formulation generally overlook misspecification of the elements of the inverse problem, such as the prior or the measurement uncertainties. This work presents an efficient algorithmic approach for designing optimal experimental design schemes for Bayesian inverse problems such that the optimal design is robust to misspecification of elements of the inverse problem. Specifically, we consider a worst-case scenario approach for the uncertain or misspecified parameters, formulate robust objectives, and propose an algorithmic approach for optimizing such objectives. Both relaxation and stochastic solution approaches are discussed with detailed analysis and insight into the interpretation of the problem and the proposed algorithmic approach. Extensive numerical experiments to validate and analyze the proposed approach are carried out for sensor placement in a parameter identification problem.

Stochastic Learning Approach to Binary Optimization for Optimal Design of Experiments

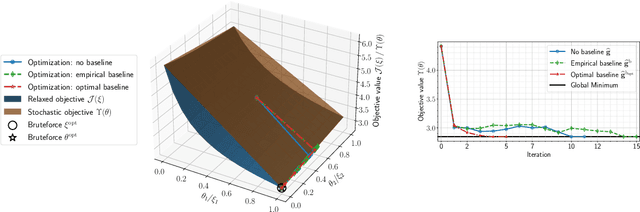
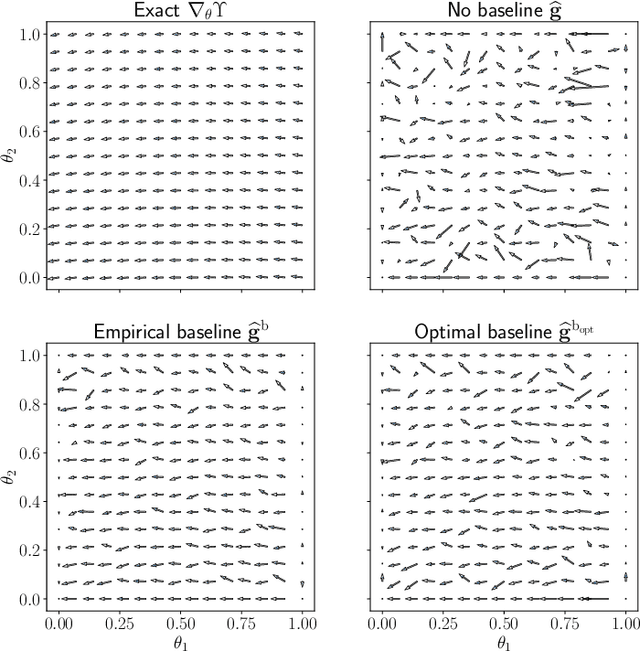
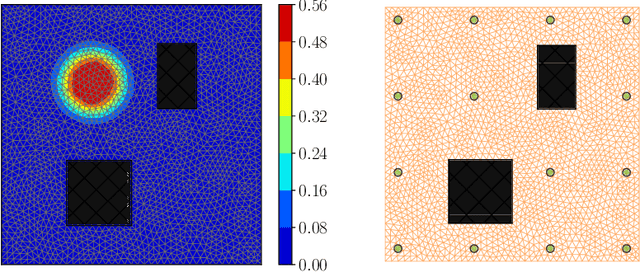
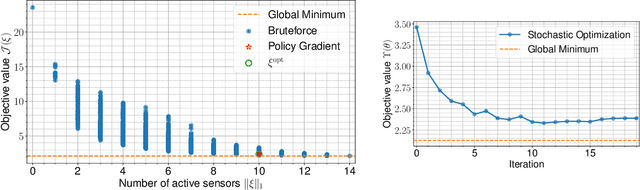
We present a novel stochastic approach to binary optimization for optimal experimental design (OED) for Bayesian inverse problems governed by mathematical models such as partial differential equations. The OED utility function, namely, the regularized optimality criterion, is cast into a stochastic objective function in the form of an expectation over a multivariate Bernoulli distribution. The probabilistic objective is then solved by using a stochastic optimization routine to find an optimal observational policy. The proposed approach is analyzed from an optimization perspective and also from a machine learning perspective with correspondence to policy gradient reinforcement learning. The approach is demonstrated numerically by using an idealized two-dimensional Bayesian linear inverse problem, and validated by extensive numerical experiments carried out for sensor placement in a parameter identification setup.

A Machine Learning Approach to Adaptive Covariance Localization

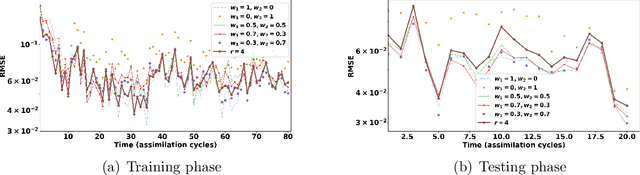
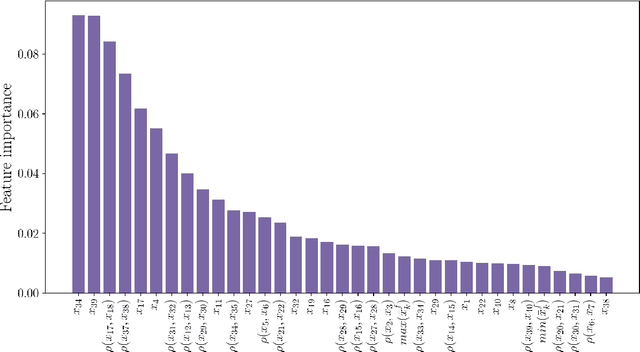
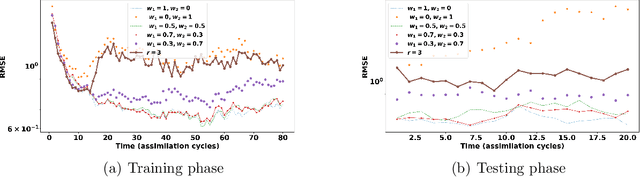
Data assimilation plays a key role in large-scale atmospheric weather forecasting, where the state of the physical system is estimated from model outputs and observations, and is then used as initial condition to produce accurate future forecasts. The Ensemble Kalman Filter (EnKF) provides a practical implementation of the statistical solution of the data assimilation problem and has gained wide popularity as. This success can be attributed to its simple formulation and ease of implementation. EnKF is a Monte-Carlo algorithm that solves the data assimilation problem by sampling the probability distributions involved in Bayes theorem. Because of this, all flavors of EnKF are fundamentally prone to sampling errors when the ensemble size is small. In typical weather forecasting applications, the model state space has dimension $10^{9}-10^{12}$, while the ensemble size typically ranges between $30-100$ members. Sampling errors manifest themselves as long-range spurious correlations and have been shown to cause filter divergence. To alleviate this effect covariance localization dampens spurious correlations between state variables located at a large distance in the physical space, via an empirical distance-dependent function. The quality of the resulting analysis and forecast is greatly influenced by the choice of the localization function parameters, e.g., the radius of influence. The localization radius is generally tuned empirically to yield desirable results.This work, proposes two adaptive algorithms for covariance localization in the EnKF framework, both based on a machine learning approach. The first algorithm adapts the localization radius in time, while the second algorithm tunes the localization radius in both time and space. Numerical experiments carried out with the Lorenz-96 model, and a quasi-geostrophic model, reveal the potential of the proposed machine learning approaches.