A Bilevel Optimization Framework for Imbalanced Data Classification

Data rebalancing techniques, including oversampling and undersampling, are a common approach to addressing the challenges of imbalanced data. To tackle unresolved problems related to both oversampling and undersampling, we propose a new undersampling approach that: (i) avoids the pitfalls of noise and overlap caused by synthetic data and (ii) avoids the pitfall of under-fitting caused by random undersampling. Instead of undersampling majority data randomly, our method undersamples datapoints based on their ability to improve model loss. Using improved model loss as a proxy measurement for classification performance, our technique assesses a datapoint's impact on loss and rejects those unable to improve it. In so doing, our approach rejects majority datapoints redundant to datapoints already accepted and, thereby, finds an optimal subset of majority training data for classification. The accept/reject component of our algorithm is motivated by a bilevel optimization problem uniquely formulated to identify the optimal training set we seek. Experimental results show our proposed technique with F1 scores up to 10% higher than state-of-the-art methods.

Robust A-Optimal Experimental Design for Bayesian Inverse Problems

Optimal design of experiments for Bayesian inverse problems has recently gained wide popularity and attracted much attention, especially in the computational science and Bayesian inversion communities. An optimal design maximizes a predefined utility function that is formulated in terms of the elements of an inverse problem, an example being optimal sensor placement for parameter identification. The state-of-the-art algorithmic approaches following this simple formulation generally overlook misspecification of the elements of the inverse problem, such as the prior or the measurement uncertainties. This work presents an efficient algorithmic approach for designing optimal experimental design schemes for Bayesian inverse problems such that the optimal design is robust to misspecification of elements of the inverse problem. Specifically, we consider a worst-case scenario approach for the uncertain or misspecified parameters, formulate robust objectives, and propose an algorithmic approach for optimizing such objectives. Both relaxation and stochastic solution approaches are discussed with detailed analysis and insight into the interpretation of the problem and the proposed algorithmic approach. Extensive numerical experiments to validate and analyze the proposed approach are carried out for sensor placement in a parameter identification problem.

Modeling Design and Control Problems Involving Neural Network Surrogates

We consider nonlinear optimization problems that involve surrogate models represented by neural networks. We demonstrate first how to directly embed neural network evaluation into optimization models, highlight a difficulty with this approach that can prevent convergence, and then characterize stationarity of such models. We then present two alternative formulations of these problems in the specific case of feedforward neural networks with ReLU activation: as a mixed-integer optimization problem and as a mathematical program with complementarity constraints. For the latter formulation we prove that stationarity at a point for this problem corresponds to stationarity of the embedded formulation. Each of these formulations may be solved with state-of-the-art optimization methods, and we show how to obtain good initial feasible solutions for these methods. We compare our formulations on three practical applications arising in the design and control of combustion engines, in the generation of adversarial attacks on classifier networks, and in the determination of optimal flows in an oil well network.

Learning Symbolic Expressions: Mixed-Integer Formulations, Cuts, and Heuristics

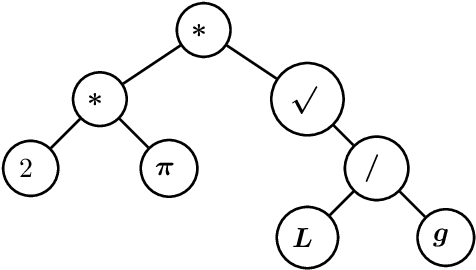
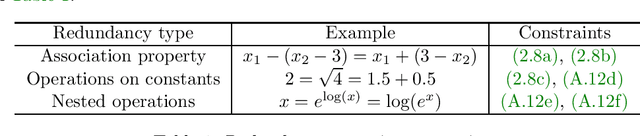
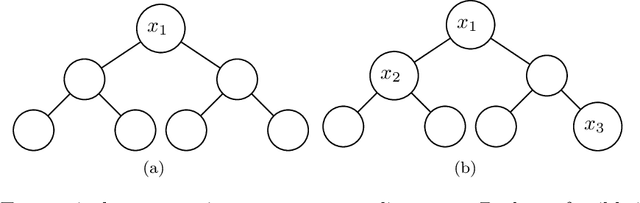
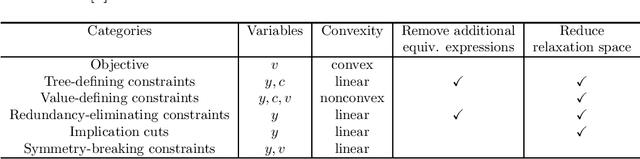
In this paper we consider the problem of learning a regression function without assuming its functional form. This problem is referred to as symbolic regression. An expression tree is typically used to represent a solution function, which is determined by assigning operators and operands to the nodes. The symbolic regression problem can be formulated as a nonconvex mixed-integer nonlinear program (MINLP), where binary variables are used to assign operators and nonlinear expressions are used to propagate data values through nonlinear operators such as square, square root, and exponential. We extend this formulation by adding new cuts that improve the solution of this challenging MINLP. We also propose a heuristic that iteratively builds an expression tree by solving a restricted MINLP. We perform computational experiments and compare our approach with a mixed-integer program-based method and a neural-network-based method from the literature.

Stochastic Learning Approach to Binary Optimization for Optimal Design of Experiments

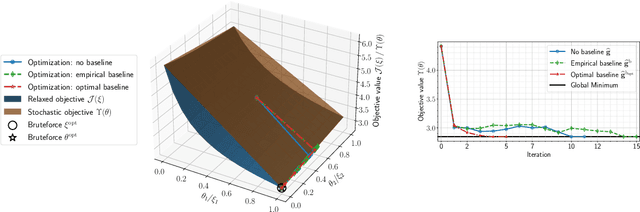
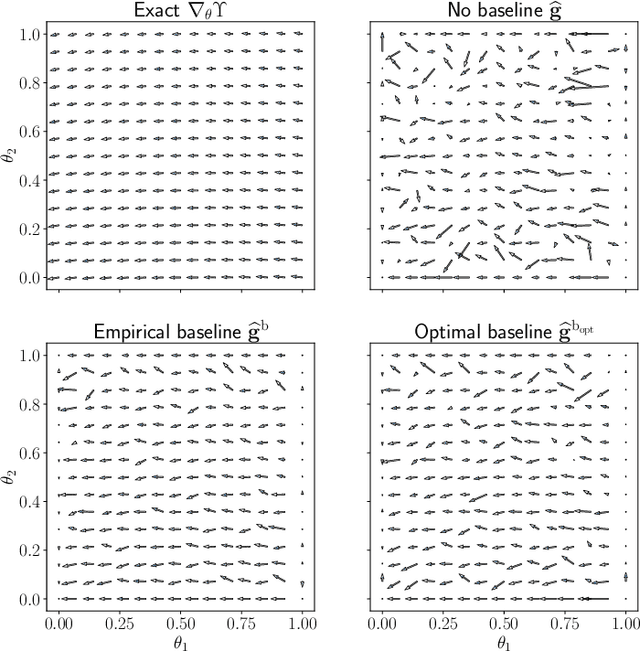
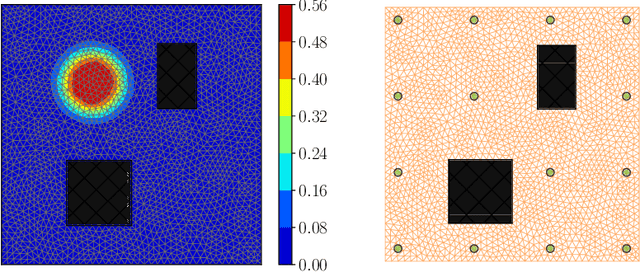
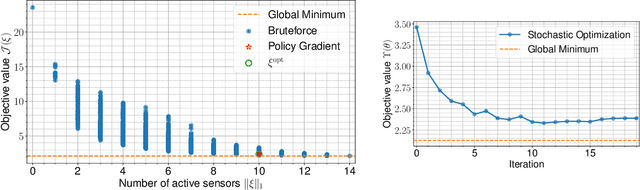
We present a novel stochastic approach to binary optimization for optimal experimental design (OED) for Bayesian inverse problems governed by mathematical models such as partial differential equations. The OED utility function, namely, the regularized optimality criterion, is cast into a stochastic objective function in the form of an expectation over a multivariate Bernoulli distribution. The probabilistic objective is then solved by using a stochastic optimization routine to find an optimal observational policy. The proposed approach is analyzed from an optimization perspective and also from a machine learning perspective with correspondence to policy gradient reinforcement learning. The approach is demonstrated numerically by using an idealized two-dimensional Bayesian linear inverse problem, and validated by extensive numerical experiments carried out for sensor placement in a parameter identification setup.