Robust A-Optimal Experimental Design for Bayesian Inverse Problems
Paper and Code
May 05, 2023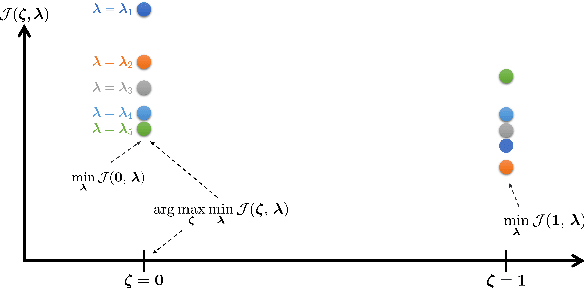
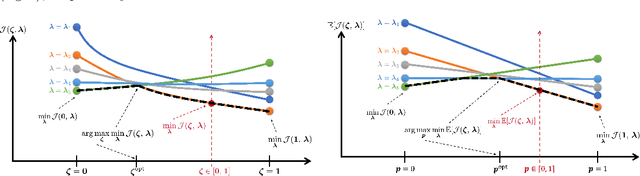
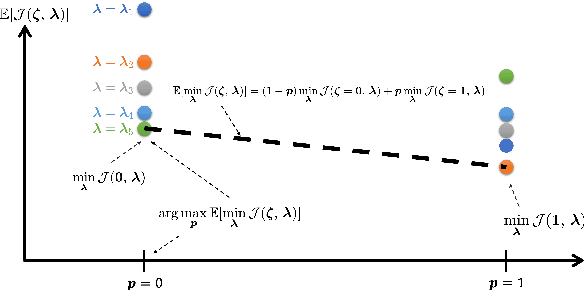
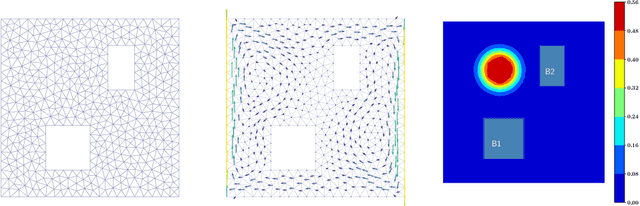
Optimal design of experiments for Bayesian inverse problems has recently gained wide popularity and attracted much attention, especially in the computational science and Bayesian inversion communities. An optimal design maximizes a predefined utility function that is formulated in terms of the elements of an inverse problem, an example being optimal sensor placement for parameter identification. The state-of-the-art algorithmic approaches following this simple formulation generally overlook misspecification of the elements of the inverse problem, such as the prior or the measurement uncertainties. This work presents an efficient algorithmic approach for designing optimal experimental design schemes for Bayesian inverse problems such that the optimal design is robust to misspecification of elements of the inverse problem. Specifically, we consider a worst-case scenario approach for the uncertain or misspecified parameters, formulate robust objectives, and propose an algorithmic approach for optimizing such objectives. Both relaxation and stochastic solution approaches are discussed with detailed analysis and insight into the interpretation of the problem and the proposed algorithmic approach. Extensive numerical experiments to validate and analyze the proposed approach are carried out for sensor placement in a parameter identification problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge