Learning Symbolic Expressions: Mixed-Integer Formulations, Cuts, and Heuristics
Paper and Code
Feb 24, 2021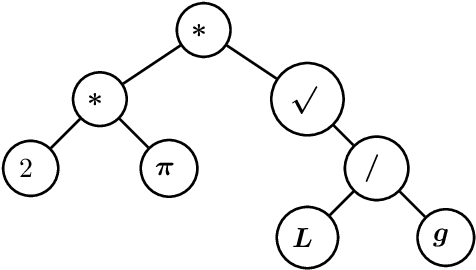
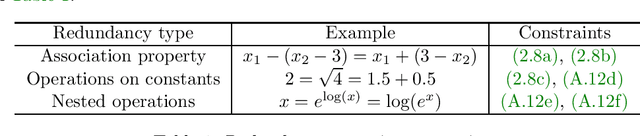
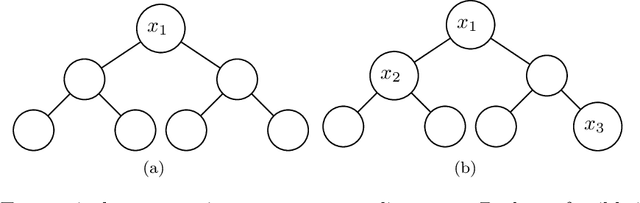
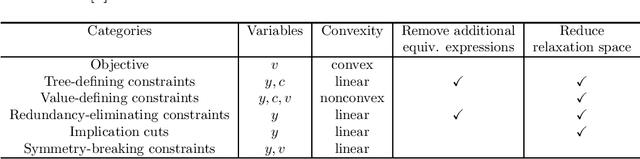
In this paper we consider the problem of learning a regression function without assuming its functional form. This problem is referred to as symbolic regression. An expression tree is typically used to represent a solution function, which is determined by assigning operators and operands to the nodes. The symbolic regression problem can be formulated as a nonconvex mixed-integer nonlinear program (MINLP), where binary variables are used to assign operators and nonlinear expressions are used to propagate data values through nonlinear operators such as square, square root, and exponential. We extend this formulation by adding new cuts that improve the solution of this challenging MINLP. We also propose a heuristic that iteratively builds an expression tree by solving a restricted MINLP. We perform computational experiments and compare our approach with a mixed-integer program-based method and a neural-network-based method from the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge