Improving the Adaptive Moment Estimation (ADAM) stochastic optimizer through an Implicit-Explicit (IMEX) time-stepping approach

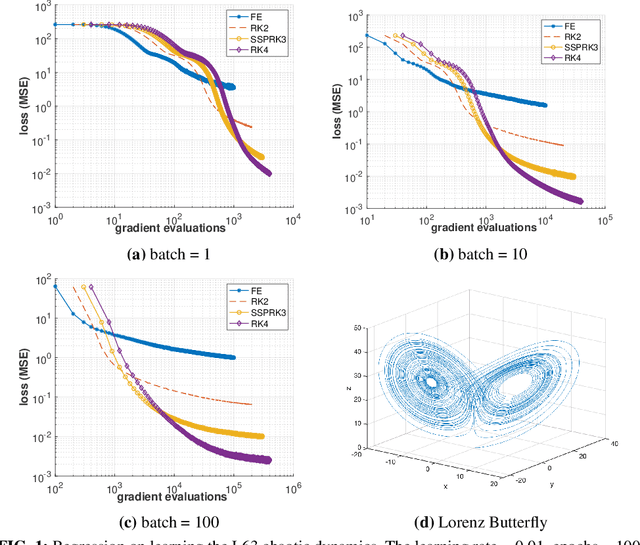
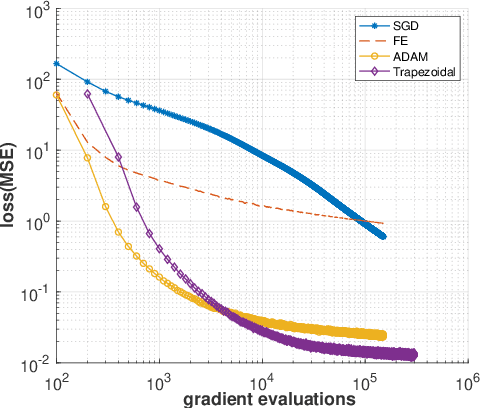
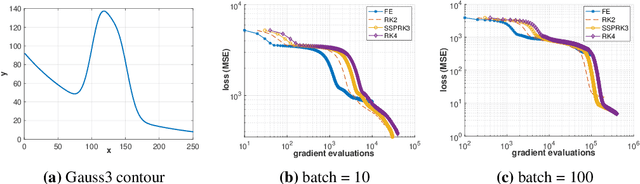
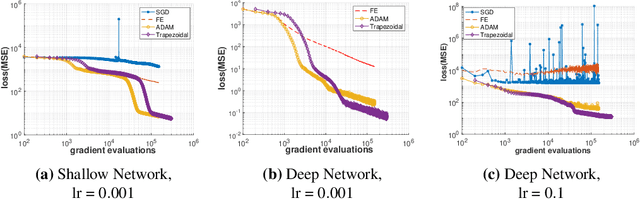
The Adam optimizer, often used in Machine Learning for neural network training, corresponds to an underlying ordinary differential equation (ODE) in the limit of very small learning rates. This work shows that the classical Adam algorithm is a first order implicit-explicit (IMEX) Euler discretization of the underlying ODE. Employing the time discretization point of view, we propose new extensions of the Adam scheme obtained by using higher order IMEX methods to solve the ODE. Based on this approach, we derive a new optimization algorithm for neural network training that performs better than classical Adam on several regression and classification problems.

Adversarial Training Using Feedback Loops

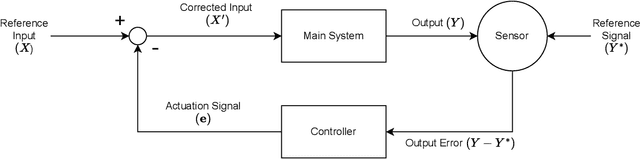
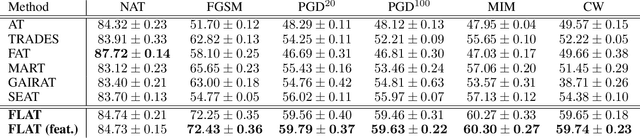
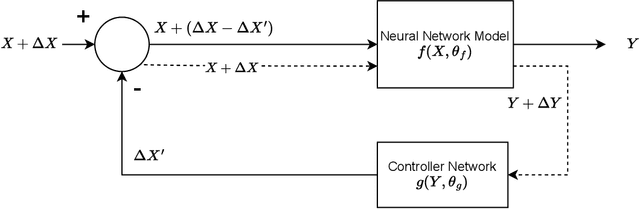
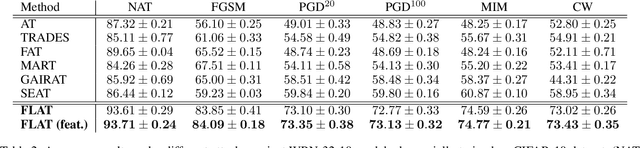
Deep neural networks (DNN) have found wide applicability in numerous fields due to their ability to accurately learn very complex input-output relations. Despite their accuracy and extensive use, DNNs are highly susceptible to adversarial attacks due to limited generalizability. For future progress in the field, it is essential to build DNNs that are robust to any kind of perturbations to the data points. In the past, many techniques have been proposed to robustify DNNs using first-order derivative information of the network. This paper proposes a new robustification approach based on control theory. A neural network architecture that incorporates feedback control, named Feedback Neural Networks, is proposed. The controller is itself a neural network, which is trained using regular and adversarial data such as to stabilize the system outputs. The novel adversarial training approach based on the feedback control architecture is called Feedback Looped Adversarial Training (FLAT). Numerical results on standard test problems empirically show that our FLAT method is more effective than the state-of-the-art to guard against adversarial attacks.

Neural Network Reduction with Guided Regularizers

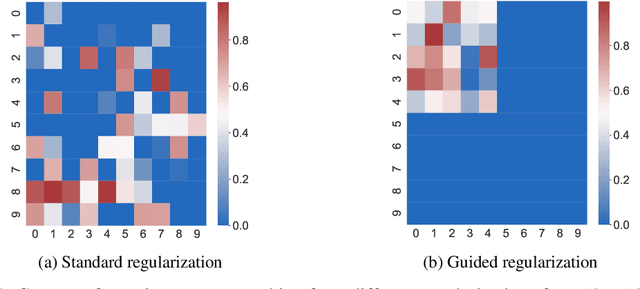
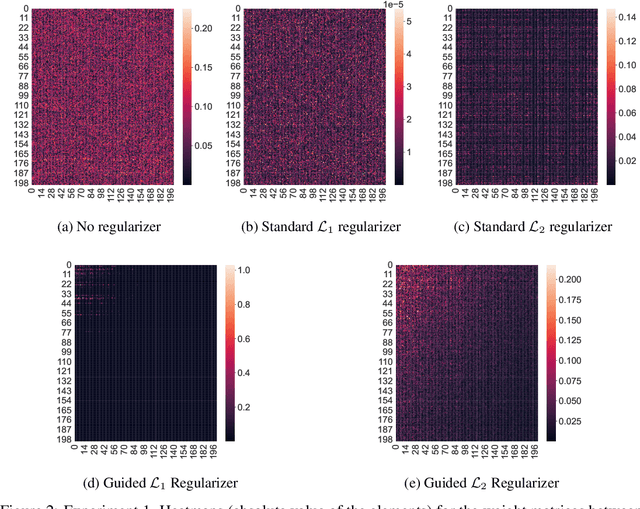
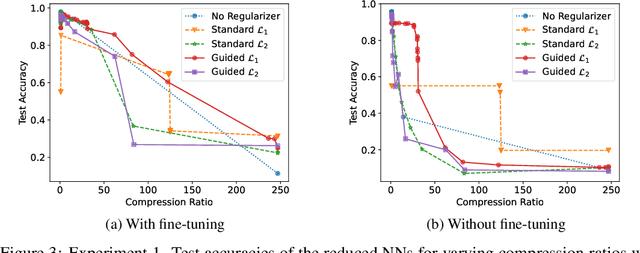
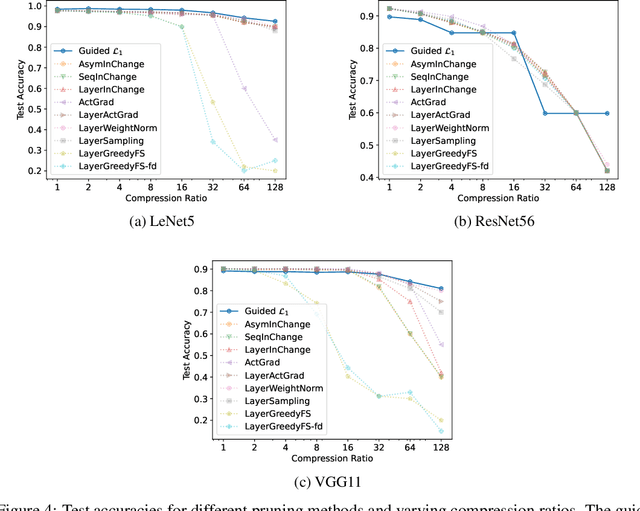
Regularization techniques such as $\mathcal{L}_1$ and $\mathcal{L}_2$ regularizers are effective in sparsifying neural networks (NNs). However, to remove a certain neuron or channel in NNs, all weight elements related to that neuron or channel need to be prunable, which is not guaranteed by traditional regularization. This paper proposes a simple new approach named "Guided Regularization" that prioritizes the weights of certain NN units more than others during training, which renders some of the units less important and thus, prunable. This is different from the scattered sparsification of $\mathcal{L}_1$ and $\mathcal{L}_2$ regularizers where the the components of a weight matrix that are zeroed out can be located anywhere. The proposed approach offers a natural reduction of NN in the sense that a model is being trained while also neutralizing unnecessary units. We empirically demonstrate that our proposed method is effective in pruning NNs while maintaining performance.

A Meta-learning Formulation of the Autoencoder Problem

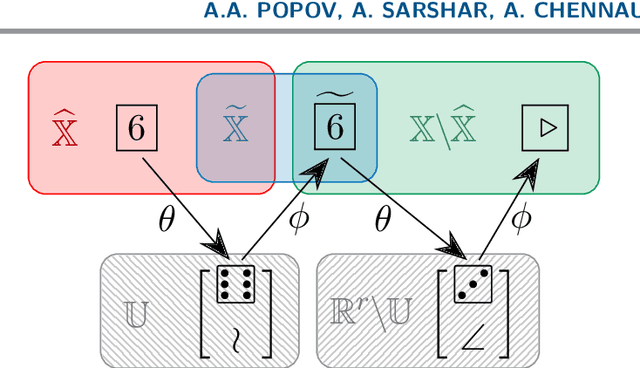
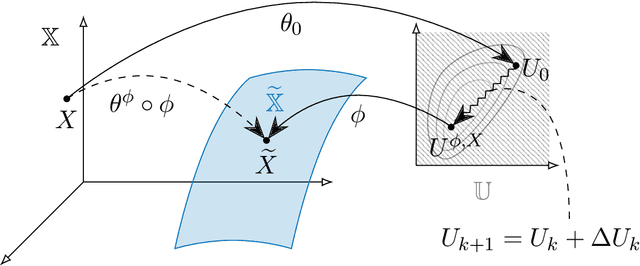
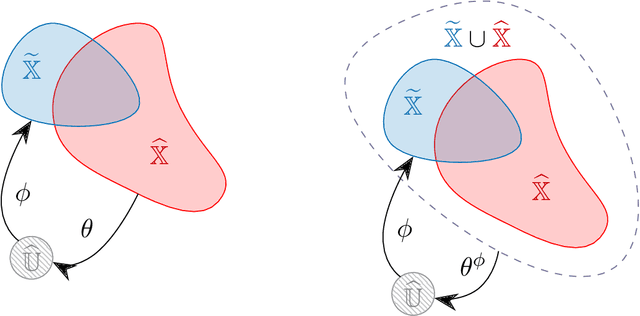
A rapidly growing area of research is the use of machine learning approaches such as autoencoders for dimensionality reduction of data and models in scientific applications. We show that the canonical formulation of autoencoders suffers from several deficiencies that can hinder their performance. Using a meta-learning approach, we reformulate the autoencoder problem as a bi-level optimization procedure that explicitly solves the dimensionality reduction task. We prove that the new formulation corrects the identified deficiencies with canonical autoencoders, provide a practical way to solve it, and showcase the strength of this formulation with a simple numerical illustration.

Physics-informed neural networks for PDE-constrained optimization and control

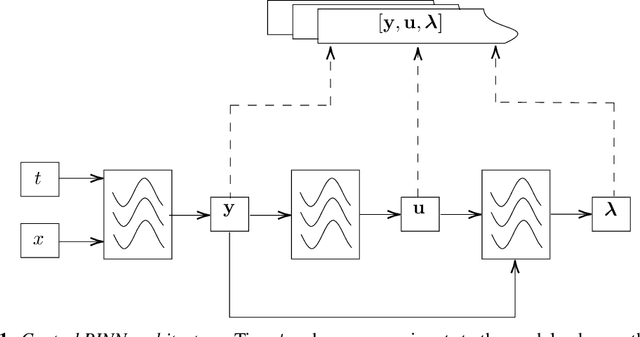
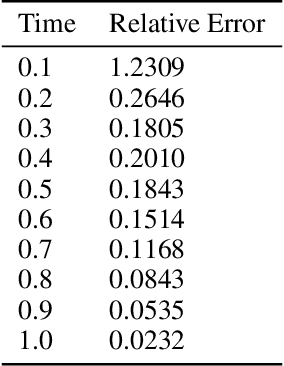
A fundamental problem of science is designing optimal control policies that manipulate a given environment into producing a desired outcome. Control Physics-Informed Neural Networks simultaneously solve a given system state, and its respective optimal control, in a one-stage framework that conforms to physical laws of the system. Prior approaches use a two-stage framework that models and controls a system sequentially, whereas Control PINNs incorporates the required optimality conditions in its architecture and loss function. The success of Control PINNs is demonstrated by solving the following open-loop optimal control problems: (i) an analytical problem (ii) a one-dimensional heat equation, and (iii) a two-dimensional predator-prey problem.

Adjoint-Matching Neural Network Surrogates for Fast 4D-Var Data Assimilation

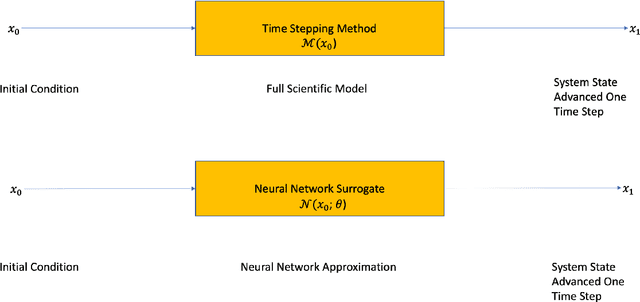
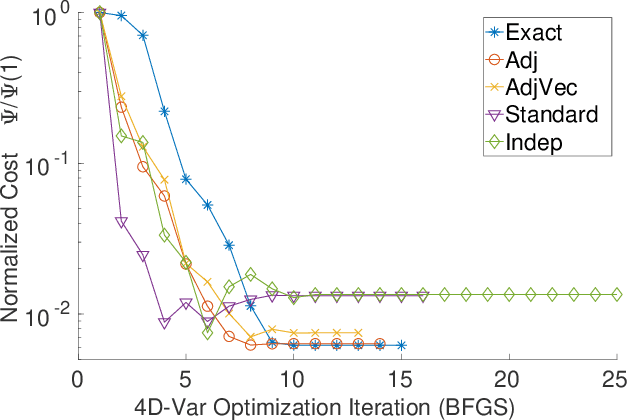
The data assimilation procedures used in many operational numerical weather forecasting systems are based around variants of the 4D-Var algorithm. The cost of solving the 4D-Var problem is dominated by the cost of forward and adjoint evaluations of the physical model. This motivates their substitution by fast, approximate surrogate models. Neural networks offer a promising approach for the data-driven creation of surrogate models. The accuracy of the surrogate 4D-Var problem's solution has been shown to depend explicitly on accurate modeling of the forward and adjoint for other surrogate modeling approaches and in the general nonlinear setting. We formulate and analyze several approaches to incorporating derivative information into the construction of neural network surrogates. The resulting networks are tested on out of training set data and in a sequential data assimilation setting on the Lorenz-63 system. Two methods demonstrate superior performance when compared with a surrogate network trained without adjoint information, showing the benefit of incorporating adjoint information into the training process.

Investigation of Nonlinear Model Order Reduction of the Quasigeostrophic Equations through a Physics-Informed Convolutional Autoencoder

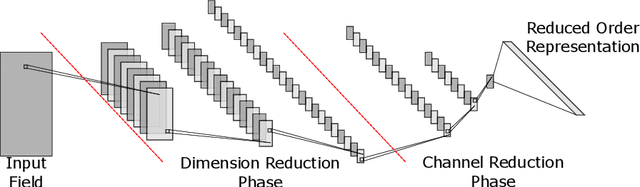
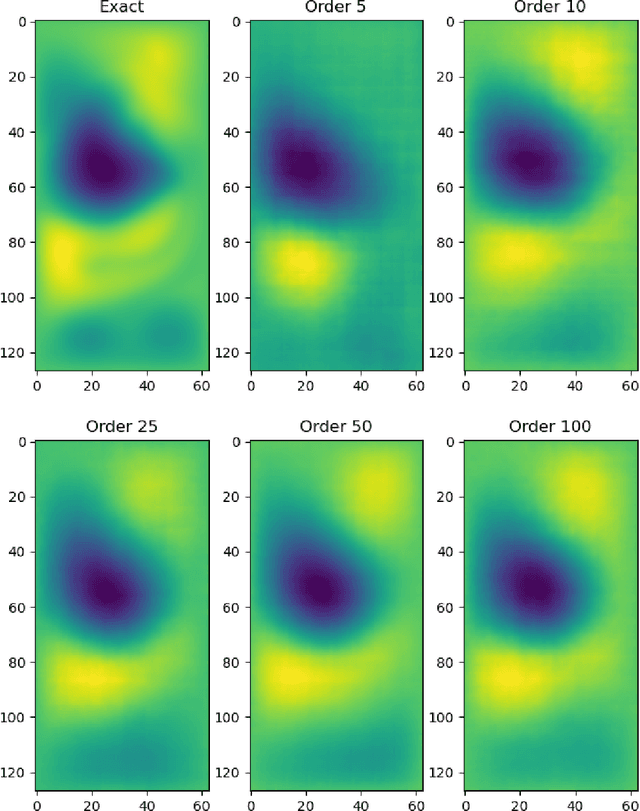
Reduced order modeling (ROM) is a field of techniques that approximates complex physics-based models of real-world processes by inexpensive surrogates that capture important dynamical characteristics with a smaller number of degrees of freedom. Traditional ROM techniques such as proper orthogonal decomposition (POD) focus on linear projections of the dynamics onto a set of spectral features. In this paper we explore the construction of ROM using autoencoders (AE) that perform nonlinear projections of the system dynamics onto a low dimensional manifold learned from data. The approach uses convolutional neural networks (CNN) to learn spatial features as opposed to spectral, and utilize a physics informed (PI) cost function in order to capture temporal features as well. Our investigation using the quasi-geostrophic equations reveals that while the PI cost function helps with spatial reconstruction, spatial features are less powerful than spectral features, and that construction of ROMs through machine learning-based methods requires significant investigation into novel non-standard methodologies.

Multifidelity Ensemble Kalman Filtering Using Surrogate Models Defined by Physics-Informed Autoencoders

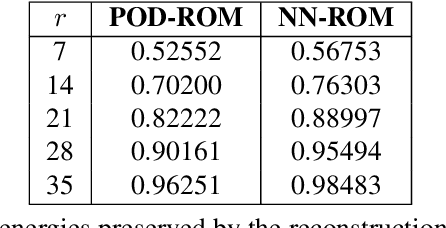
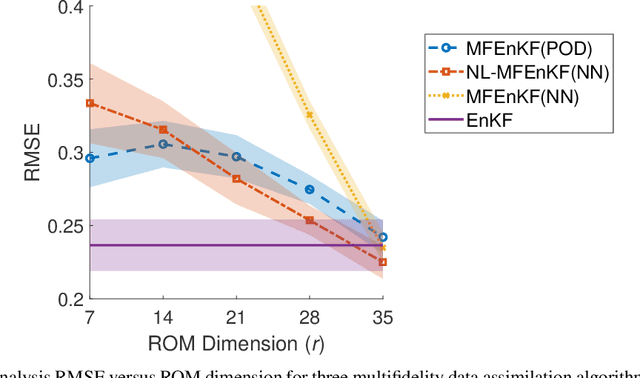
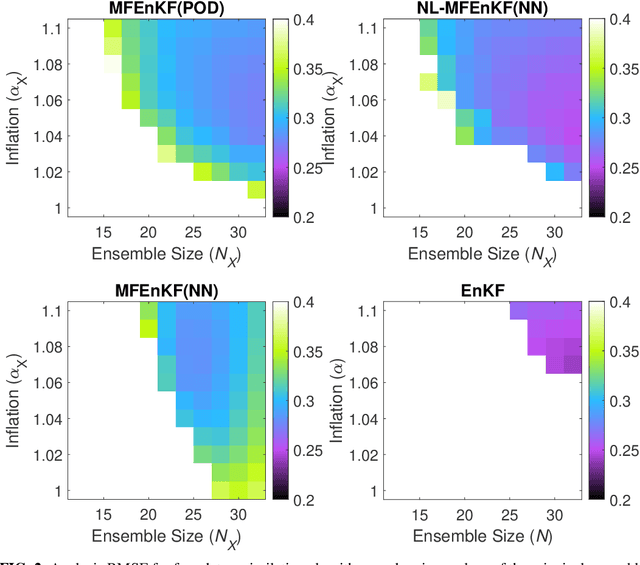
Data assimilation is a Bayesian inference process that obtains an enhanced understanding of a physical system of interest by fusing information from an inexact physics-based model, and from noisy sparse observations of reality. The multifidelity ensemble Kalman filter (MFEnKF) recently developed by the authors combines a full-order physical model and a hierarchy of reduced order surrogate models in order to increase the computational efficiency of data assimilation. The standard MFEnKF uses linear couplings between models, and is statistically optimal in case of Gaussian probability densities. This work extends MFEnKF to work with non-linear couplings between the models. Optimal nonlinear projection and interpolation operators are obtained by appropriately trained physics-informed autoencoders, and this approach allows to construct reduced order surrogate models with less error than conventional linear methods. Numerical experiments with the canonical Lorenz '96 model illustrate that nonlinear surrogates perform better than linear projection-based ones in the context of multifidelity filtering.

A Machine Learning Approach to Adaptive Covariance Localization

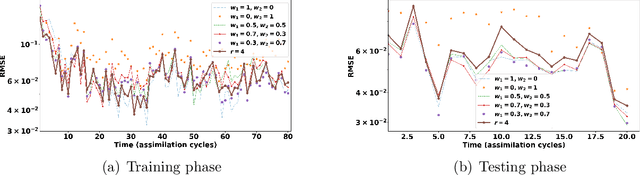
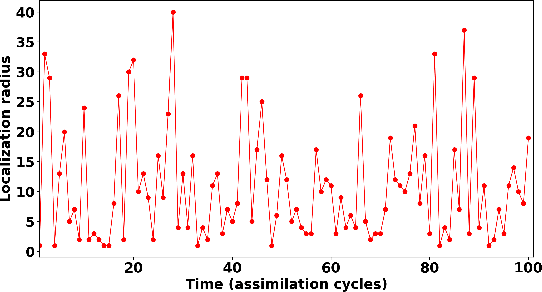
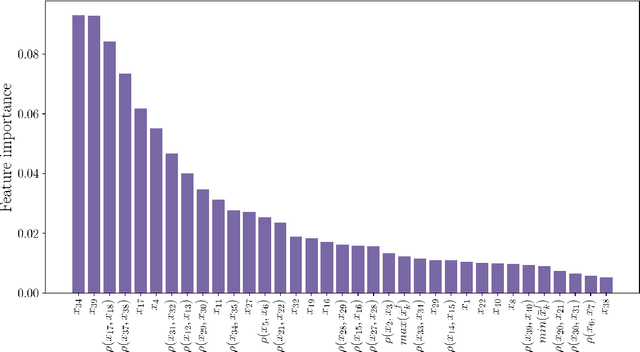
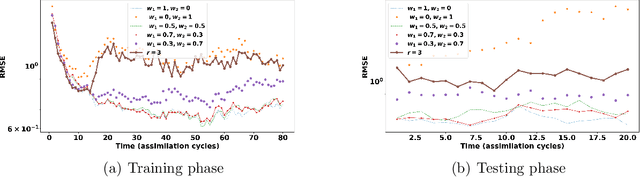
Data assimilation plays a key role in large-scale atmospheric weather forecasting, where the state of the physical system is estimated from model outputs and observations, and is then used as initial condition to produce accurate future forecasts. The Ensemble Kalman Filter (EnKF) provides a practical implementation of the statistical solution of the data assimilation problem and has gained wide popularity as. This success can be attributed to its simple formulation and ease of implementation. EnKF is a Monte-Carlo algorithm that solves the data assimilation problem by sampling the probability distributions involved in Bayes theorem. Because of this, all flavors of EnKF are fundamentally prone to sampling errors when the ensemble size is small. In typical weather forecasting applications, the model state space has dimension $10^{9}-10^{12}$, while the ensemble size typically ranges between $30-100$ members. Sampling errors manifest themselves as long-range spurious correlations and have been shown to cause filter divergence. To alleviate this effect covariance localization dampens spurious correlations between state variables located at a large distance in the physical space, via an empirical distance-dependent function. The quality of the resulting analysis and forecast is greatly influenced by the choice of the localization function parameters, e.g., the radius of influence. The localization radius is generally tuned empirically to yield desirable results.This work, proposes two adaptive algorithms for covariance localization in the EnKF framework, both based on a machine learning approach. The first algorithm adapts the localization radius in time, while the second algorithm tunes the localization radius in both time and space. Numerical experiments carried out with the Lorenz-96 model, and a quasi-geostrophic model, reveal the potential of the proposed machine learning approaches.

Efficient Construction of Local Parametric Reduced Order Models Using Machine Learning Techniques

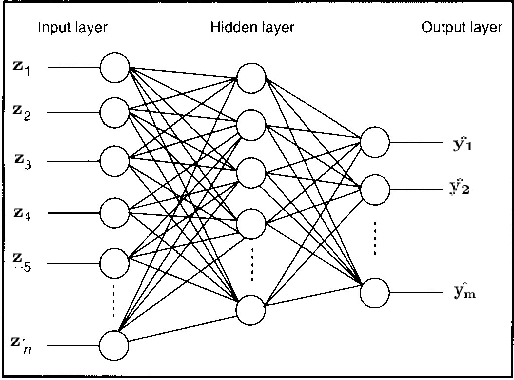
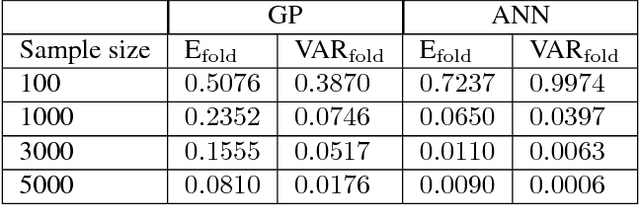
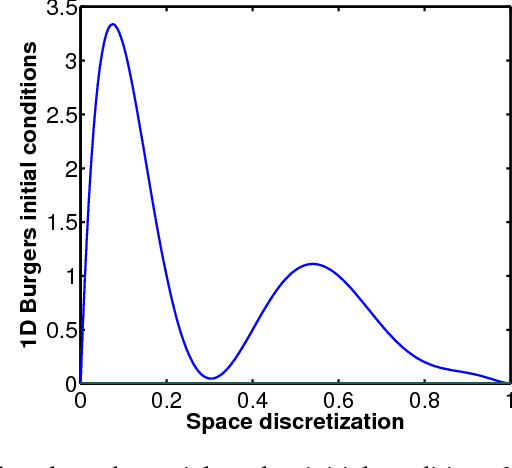
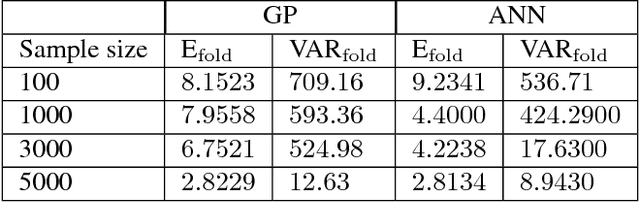
Reduced order models are computationally inexpensive approximations that capture the important dynamical characteristics of large, high-fidelity computer models of physical systems. This paper applies machine learning techniques to improve the design of parametric reduced order models. Specifically, machine learning is used to develop feasible regions in the parameter space where the admissible target accuracy is achieved with a predefined reduced order basis, to construct parametric maps, to chose the best two already existing bases for a new parameter configuration from accuracy point of view and to pre-select the optimal dimension of the reduced basis such as to meet the desired accuracy. By combining available information using bases concatenation and interpolation as well as high-fidelity solutions interpolation we are able to build accurate reduced order models associated with new parameter settings. Promising numerical results with a viscous Burgers model illustrate the potential of machine learning approaches to help design better reduced order models.