The Ensemble Epanechnikov Mixture Filter

In the high-dimensional setting, Gaussian mixture kernel density estimates become increasingly suboptimal. In this work we aim to show that it is practical to instead use the optimal multivariate Epanechnikov kernel. We make use of this optimal Epanechnikov mixture kernel density estimate for the sequential filtering scenario through what we term the ensemble Epanechnikov mixture filter (EnEMF). We provide a practical implementation of the EnEMF that is as cost efficient as the comparable ensemble Gaussian mixture filter. We show on a static example that the EnEMF is robust to growth in dimension, and also that the EnEMF has a significant reduction in error per particle on the 40-variable Lorenz '96 system.

Improving the Adaptive Moment Estimation (ADAM) stochastic optimizer through an Implicit-Explicit (IMEX) time-stepping approach

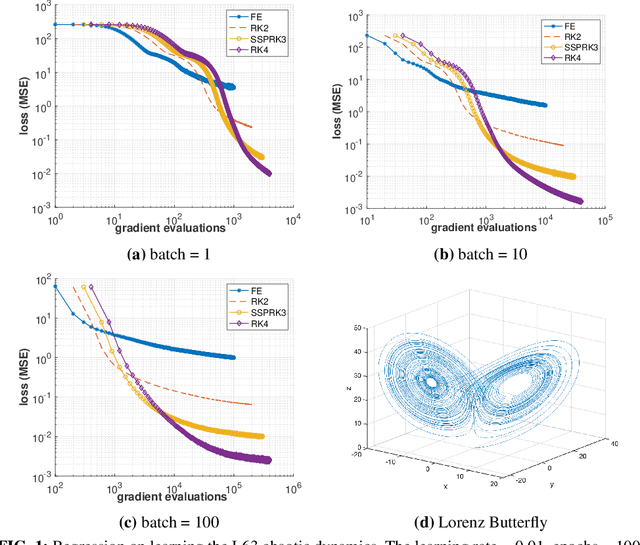
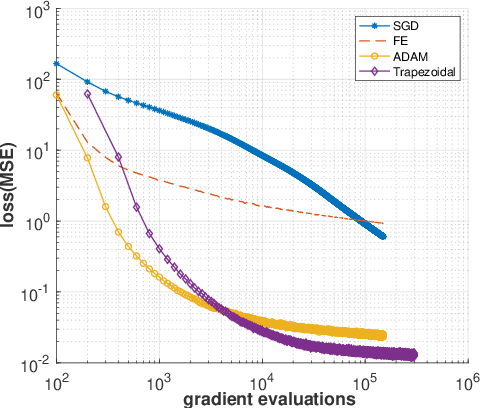
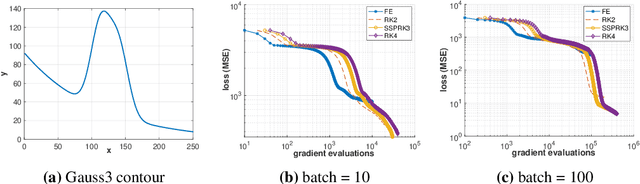
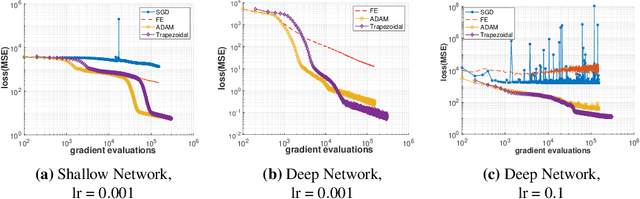
The Adam optimizer, often used in Machine Learning for neural network training, corresponds to an underlying ordinary differential equation (ODE) in the limit of very small learning rates. This work shows that the classical Adam algorithm is a first order implicit-explicit (IMEX) Euler discretization of the underlying ODE. Employing the time discretization point of view, we propose new extensions of the Adam scheme obtained by using higher order IMEX methods to solve the ODE. Based on this approach, we derive a new optimization algorithm for neural network training that performs better than classical Adam on several regression and classification problems.

Precision Mars Entry Navigation with Atmospheric Density Adaptation via Neural Networks

Discrepancies between the true Martian atmospheric density and the onboard density model can significantly impair the performance of spacecraft entry navigation filters. This work introduces a new approach to online filtering for Martian entry by using a neural network to estimate atmospheric density and employing a consider analysis to account for the uncertainty in the estimate. The network is trained on an exponential atmospheric density model, and its parameters are dynamically adapted in real time to account for any mismatches between the true and estimated densities. The adaptation of the network is formulated as a maximum likelihood problem, leveraging the measurement innovations of the filter to identify optimal network parameters. The incorporation of a neural network enables the use of stochastic optimizers known for their efficiency in the machine learning domain within the context of the maximum likelihood approach. Performance comparisons against previous approaches are conducted in various realistic Mars entry navigation scenarios, resulting in superior estimation accuracy and precise alignment of the estimated density with a broad selection of realistic Martian atmospheres sampled from perturbed Mars-GRAM data.

Small-data Reduced Order Modeling of Chaotic Dynamics through SyCo-AE: Synthetically Constrained Autoencoders

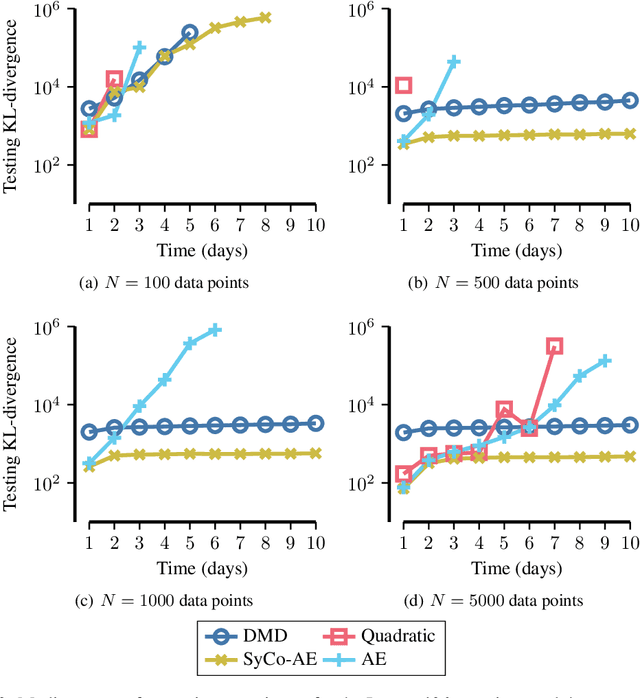
Data-driven reduced order modeling of chaotic dynamics can result in systems that either dissipate or diverge catastrophically. Leveraging non-linear dimensionality reduction of autoencoders and the freedom of non-linear operator inference with neural-networks, we aim to solve this problem by imposing a synthetic constraint in the reduced order space. The synthetic constraint allows our reduced order model both the freedom to remain fully non-linear and highly unstable while preventing divergence. We illustrate the methodology with the classical 40-variable Lorenz '96 equations, showing that our methodology is capable of producing medium-to-long range forecasts with lower error using less data.

An optimal sensors-based simulation method for spatiotemporal event detection

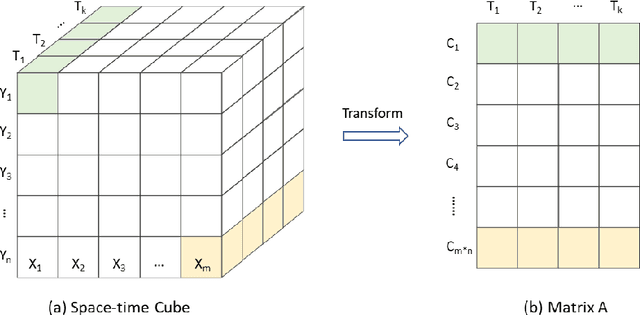
Human movements in urban areas are essential for understanding the human-environment interactions. However, activities and associated movements are full of uncertainties due to the complexity of a city. In this paper, we propose an optimal sensors-based simulation method for spatiotemporal event detection using human activity signals derived from taxi trip data. A sensor here is an abstract concept such that only the true observation data at the sensor location will be treated as known data for the simulation. Specifically, we first identify the optimal number of sensors and their locations that have the strongest correlation with the whole dataset. The observation data points from these sensors are then used to simulate a regular, uneventful scenario using the Discrete Empirical Interpolation Method. By comparing the simulated and observation scenarios, events are extracted both spatially and temporally. We apply this method in New York City with taxi trip records data. Results show that this method is effective in detecting when and where events occur.

A Meta-learning Formulation of the Autoencoder Problem

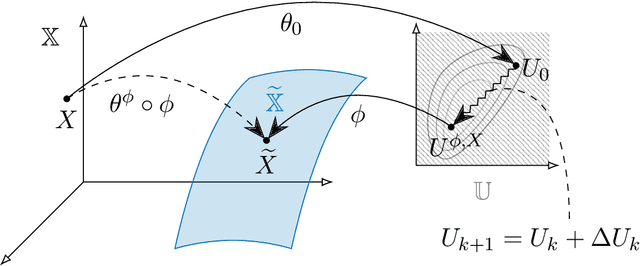
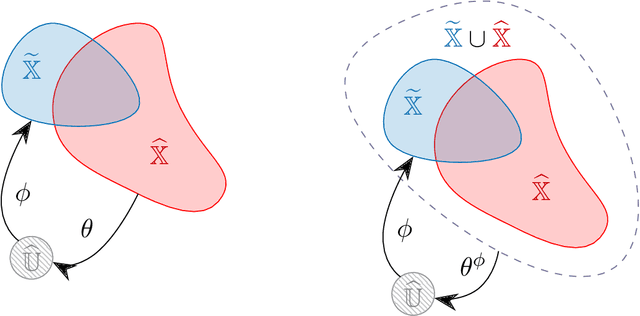
A rapidly growing area of research is the use of machine learning approaches such as autoencoders for dimensionality reduction of data and models in scientific applications. We show that the canonical formulation of autoencoders suffers from several deficiencies that can hinder their performance. Using a meta-learning approach, we reformulate the autoencoder problem as a bi-level optimization procedure that explicitly solves the dimensionality reduction task. We prove that the new formulation corrects the identified deficiencies with canonical autoencoders, provide a practical way to solve it, and showcase the strength of this formulation with a simple numerical illustration.

Physics-informed neural networks for PDE-constrained optimization and control

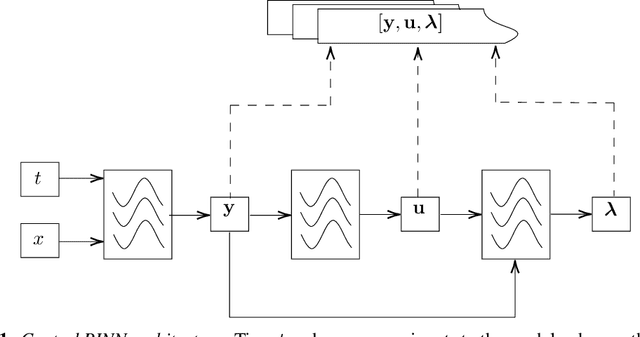
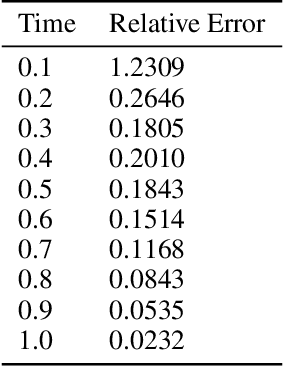
A fundamental problem of science is designing optimal control policies that manipulate a given environment into producing a desired outcome. Control Physics-Informed Neural Networks simultaneously solve a given system state, and its respective optimal control, in a one-stage framework that conforms to physical laws of the system. Prior approaches use a two-stage framework that models and controls a system sequentially, whereas Control PINNs incorporates the required optimality conditions in its architecture and loss function. The success of Control PINNs is demonstrated by solving the following open-loop optimal control problems: (i) an analytical problem (ii) a one-dimensional heat equation, and (iii) a two-dimensional predator-prey problem.

Adjoint-Matching Neural Network Surrogates for Fast 4D-Var Data Assimilation

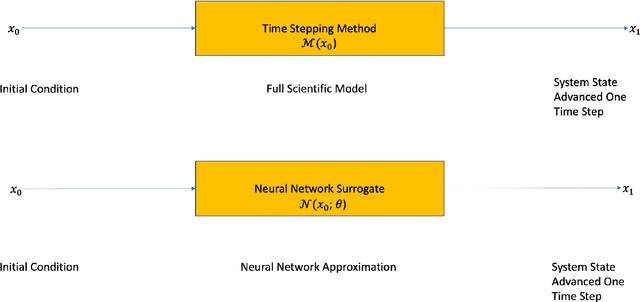
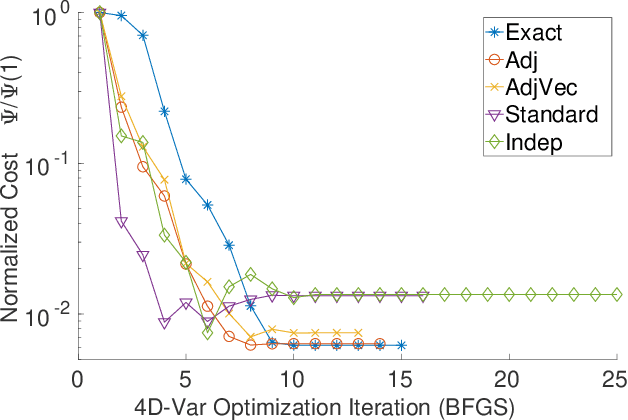
The data assimilation procedures used in many operational numerical weather forecasting systems are based around variants of the 4D-Var algorithm. The cost of solving the 4D-Var problem is dominated by the cost of forward and adjoint evaluations of the physical model. This motivates their substitution by fast, approximate surrogate models. Neural networks offer a promising approach for the data-driven creation of surrogate models. The accuracy of the surrogate 4D-Var problem's solution has been shown to depend explicitly on accurate modeling of the forward and adjoint for other surrogate modeling approaches and in the general nonlinear setting. We formulate and analyze several approaches to incorporating derivative information into the construction of neural network surrogates. The resulting networks are tested on out of training set data and in a sequential data assimilation setting on the Lorenz-63 system. Two methods demonstrate superior performance when compared with a surrogate network trained without adjoint information, showing the benefit of incorporating adjoint information into the training process.

Investigation of Nonlinear Model Order Reduction of the Quasigeostrophic Equations through a Physics-Informed Convolutional Autoencoder

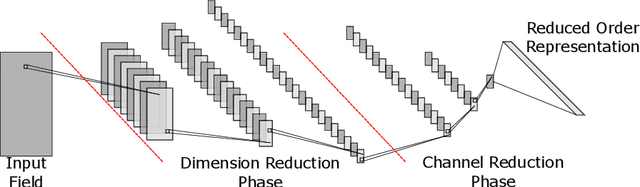
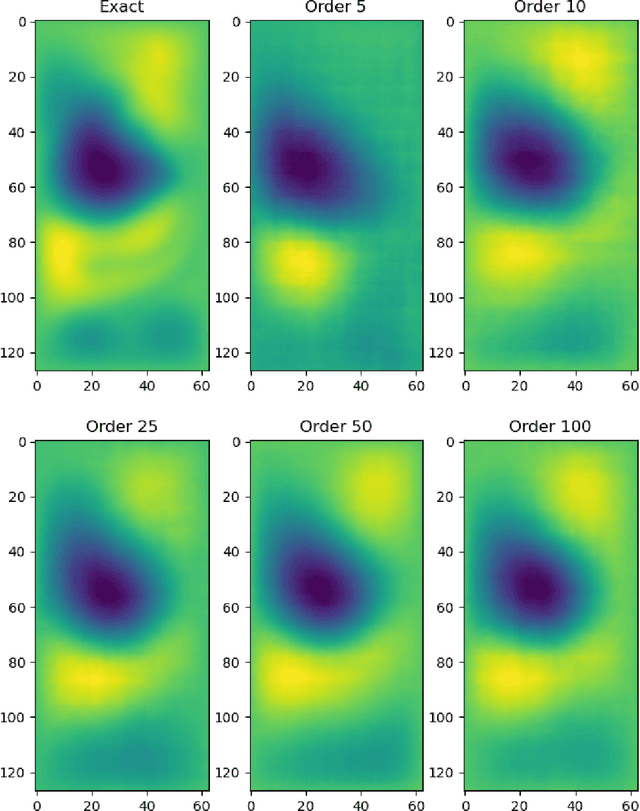
Reduced order modeling (ROM) is a field of techniques that approximates complex physics-based models of real-world processes by inexpensive surrogates that capture important dynamical characteristics with a smaller number of degrees of freedom. Traditional ROM techniques such as proper orthogonal decomposition (POD) focus on linear projections of the dynamics onto a set of spectral features. In this paper we explore the construction of ROM using autoencoders (AE) that perform nonlinear projections of the system dynamics onto a low dimensional manifold learned from data. The approach uses convolutional neural networks (CNN) to learn spatial features as opposed to spectral, and utilize a physics informed (PI) cost function in order to capture temporal features as well. Our investigation using the quasi-geostrophic equations reveals that while the PI cost function helps with spatial reconstruction, spatial features are less powerful than spectral features, and that construction of ROMs through machine learning-based methods requires significant investigation into novel non-standard methodologies.