Deep Operator Networks for Bayesian Parameter Estimation in PDEs

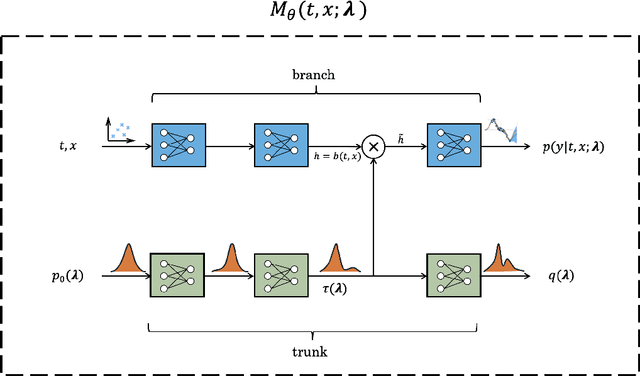
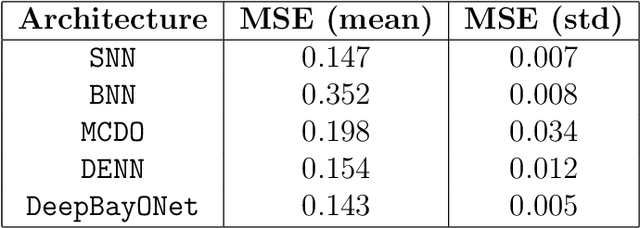
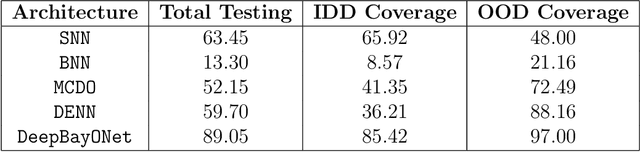
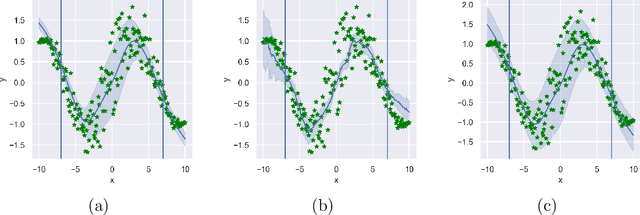
We present a novel framework combining Deep Operator Networks (DeepONets) with Physics-Informed Neural Networks (PINNs) to solve partial differential equations (PDEs) and estimate their unknown parameters. By integrating data-driven learning with physical constraints, our method achieves robust and accurate solutions across diverse scenarios. Bayesian training is implemented through variational inference, allowing for comprehensive uncertainty quantification for both aleatoric and epistemic uncertainties. This ensures reliable predictions and parameter estimates even in noisy conditions or when some of the physical equations governing the problem are missing. The framework demonstrates its efficacy in solving forward and inverse problems, including the 1D unsteady heat equation and 2D reaction-diffusion equations, as well as regression tasks with sparse, noisy observations. This approach provides a computationally efficient and generalizable method for addressing uncertainty quantification in PDE surrogate modeling.

Improving the Adaptive Moment Estimation (ADAM) stochastic optimizer through an Implicit-Explicit (IMEX) time-stepping approach

The Adam optimizer, often used in Machine Learning for neural network training, corresponds to an underlying ordinary differential equation (ODE) in the limit of very small learning rates. This work shows that the classical Adam algorithm is a first order implicit-explicit (IMEX) Euler discretization of the underlying ODE. Employing the time discretization point of view, we propose new extensions of the Adam scheme obtained by using higher order IMEX methods to solve the ODE. Based on this approach, we derive a new optimization algorithm for neural network training that performs better than classical Adam on several regression and classification problems.

A Meta-learning Formulation of the Autoencoder Problem

A rapidly growing area of research is the use of machine learning approaches such as autoencoders for dimensionality reduction of data and models in scientific applications. We show that the canonical formulation of autoencoders suffers from several deficiencies that can hinder their performance. Using a meta-learning approach, we reformulate the autoencoder problem as a bi-level optimization procedure that explicitly solves the dimensionality reduction task. We prove that the new formulation corrects the identified deficiencies with canonical autoencoders, provide a practical way to solve it, and showcase the strength of this formulation with a simple numerical illustration.

Physics-informed neural networks for PDE-constrained optimization and control

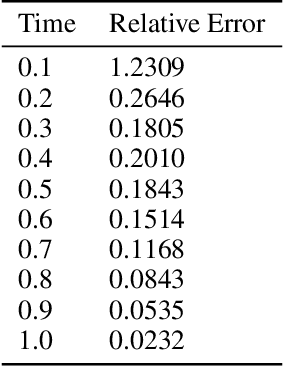
A fundamental problem of science is designing optimal control policies that manipulate a given environment into producing a desired outcome. Control Physics-Informed Neural Networks simultaneously solve a given system state, and its respective optimal control, in a one-stage framework that conforms to physical laws of the system. Prior approaches use a two-stage framework that models and controls a system sequentially, whereas Control PINNs incorporates the required optimality conditions in its architecture and loss function. The success of Control PINNs is demonstrated by solving the following open-loop optimal control problems: (i) an analytical problem (ii) a one-dimensional heat equation, and (iii) a two-dimensional predator-prey problem.