A Meta-learning Formulation of the Autoencoder Problem

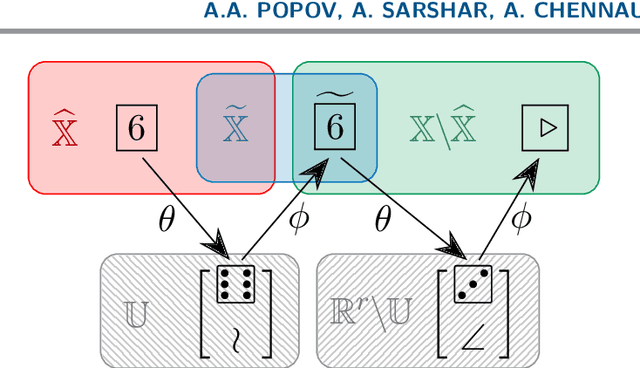
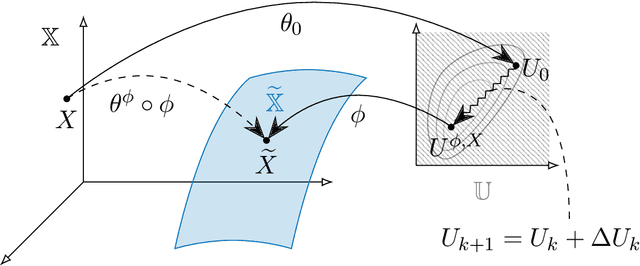
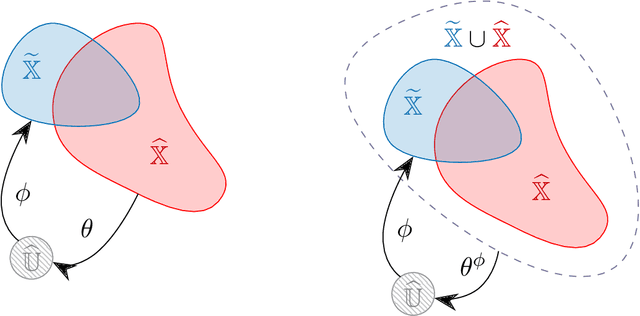
A rapidly growing area of research is the use of machine learning approaches such as autoencoders for dimensionality reduction of data and models in scientific applications. We show that the canonical formulation of autoencoders suffers from several deficiencies that can hinder their performance. Using a meta-learning approach, we reformulate the autoencoder problem as a bi-level optimization procedure that explicitly solves the dimensionality reduction task. We prove that the new formulation corrects the identified deficiencies with canonical autoencoders, provide a practical way to solve it, and showcase the strength of this formulation with a simple numerical illustration.

Adjoint-Matching Neural Network Surrogates for Fast 4D-Var Data Assimilation

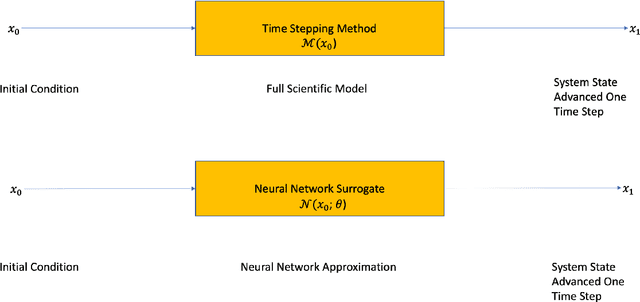
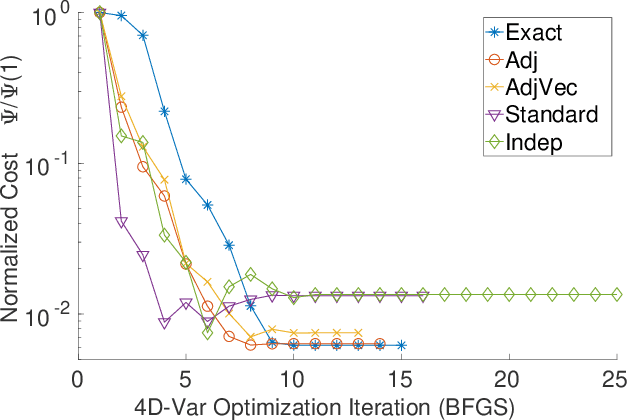
The data assimilation procedures used in many operational numerical weather forecasting systems are based around variants of the 4D-Var algorithm. The cost of solving the 4D-Var problem is dominated by the cost of forward and adjoint evaluations of the physical model. This motivates their substitution by fast, approximate surrogate models. Neural networks offer a promising approach for the data-driven creation of surrogate models. The accuracy of the surrogate 4D-Var problem's solution has been shown to depend explicitly on accurate modeling of the forward and adjoint for other surrogate modeling approaches and in the general nonlinear setting. We formulate and analyze several approaches to incorporating derivative information into the construction of neural network surrogates. The resulting networks are tested on out of training set data and in a sequential data assimilation setting on the Lorenz-63 system. Two methods demonstrate superior performance when compared with a surrogate network trained without adjoint information, showing the benefit of incorporating adjoint information into the training process.