Improving the Adaptive Moment Estimation (ADAM) stochastic optimizer through an Implicit-Explicit (IMEX) time-stepping approach

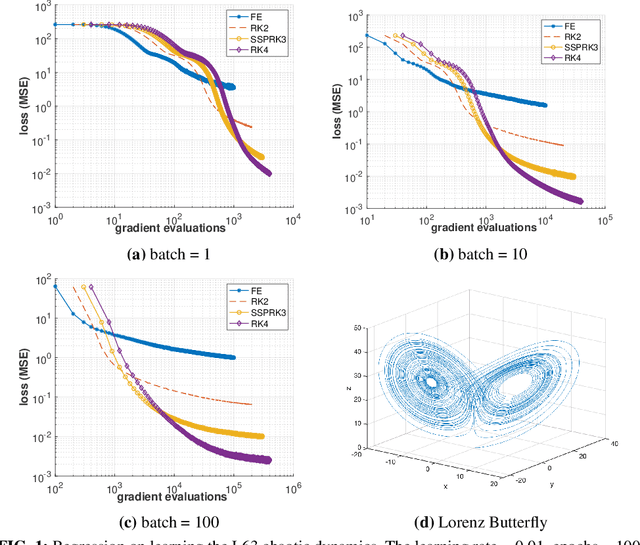
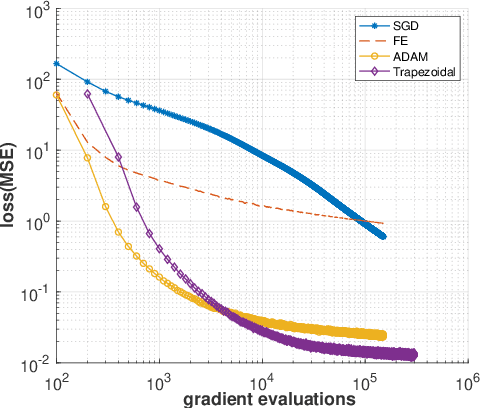
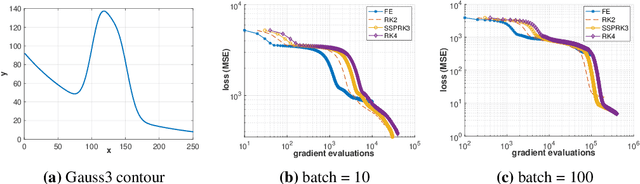
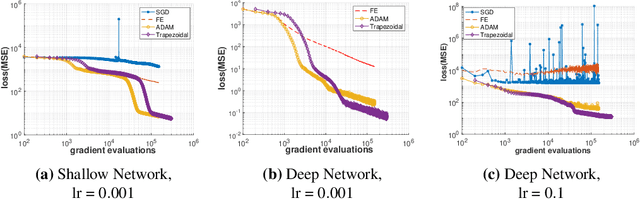
The Adam optimizer, often used in Machine Learning for neural network training, corresponds to an underlying ordinary differential equation (ODE) in the limit of very small learning rates. This work shows that the classical Adam algorithm is a first order implicit-explicit (IMEX) Euler discretization of the underlying ODE. Employing the time discretization point of view, we propose new extensions of the Adam scheme obtained by using higher order IMEX methods to solve the ODE. Based on this approach, we derive a new optimization algorithm for neural network training that performs better than classical Adam on several regression and classification problems.