Renato Zanetti
Kernel-Based Ensemble Gaussian Mixture Probability Hypothesis Density Filter
Apr 30, 2025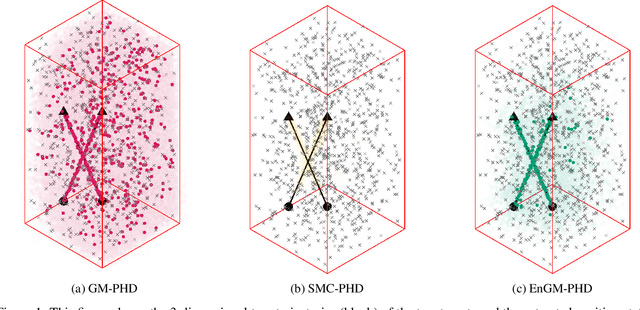
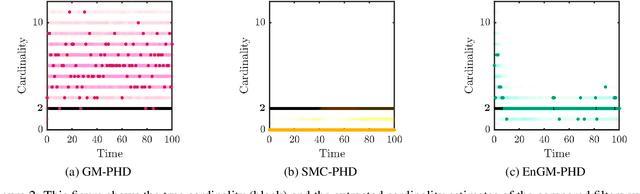
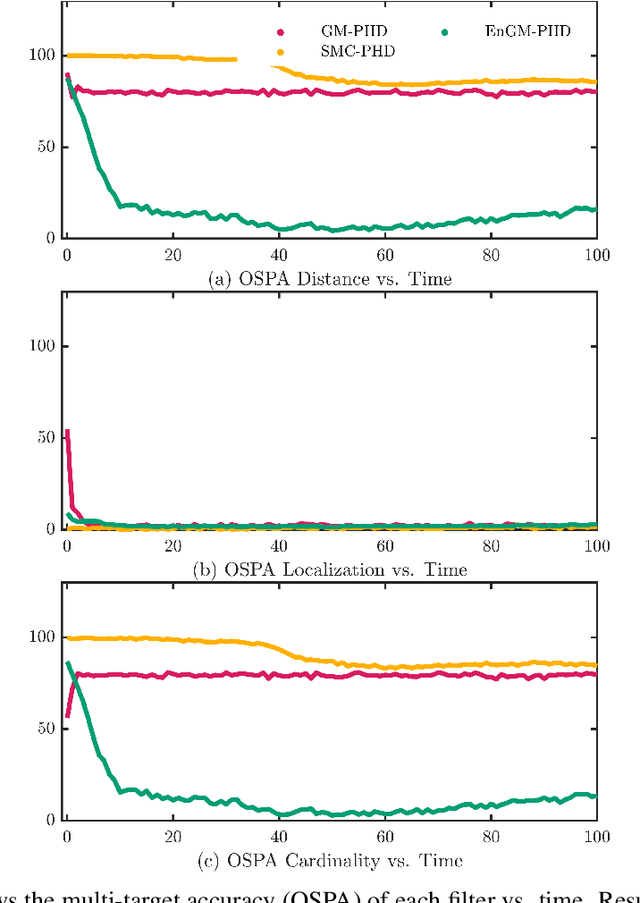
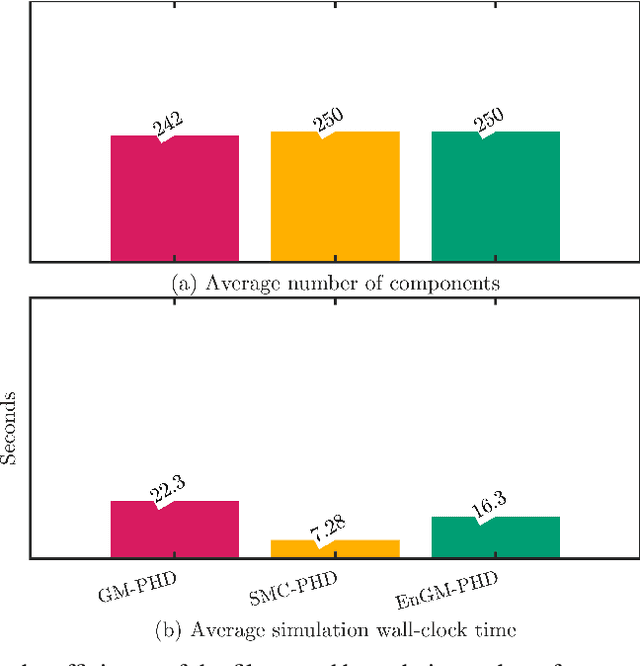
Abstract:In this work, a kernel-based Ensemble Gaussian Mixture Probability Hypothesis Density (EnGM-PHD) filter is presented for multi-target filtering applications. The EnGM-PHD filter combines the Gaussian-mixture-based techniques of the Gaussian Mixture Probability Hypothesis Density (GM-PHD) filter with the particle-based techniques of the Sequential Monte Carlo Probability Hypothesis Density (SMC-PHD) filter. It achieves this by obtaining particles from the posterior intensity function, propagating them through the system dynamics, and then using Kernel Density Estimation (KDE) techniques to approximate the Gaussian mixture of the prior intensity function. This approach guarantees convergence to the true intensity function in the limit of the number of components. Moreover, in the special case of a single target with no births, deaths, clutter, and perfect detection probability, the EnGM-PHD filter reduces to the standard Ensemble Gaussian Mixture Filter (EnGMF). In the presented experiment, the results indicate that the EnGM-PHD filter achieves better multi-target filtering performance than both the GM-PHD and SMC-PHD filters while using the same number of components or particles.
The Ensemble Epanechnikov Mixture Filter
Aug 20, 2024Abstract:In the high-dimensional setting, Gaussian mixture kernel density estimates become increasingly suboptimal. In this work we aim to show that it is practical to instead use the optimal multivariate Epanechnikov kernel. We make use of this optimal Epanechnikov mixture kernel density estimate for the sequential filtering scenario through what we term the ensemble Epanechnikov mixture filter (EnEMF). We provide a practical implementation of the EnEMF that is as cost efficient as the comparable ensemble Gaussian mixture filter. We show on a static example that the EnEMF is robust to growth in dimension, and also that the EnEMF has a significant reduction in error per particle on the 40-variable Lorenz '96 system.
Precision Mars Entry Navigation with Atmospheric Density Adaptation via Neural Networks
Jan 17, 2024Abstract:Discrepancies between the true Martian atmospheric density and the onboard density model can significantly impair the performance of spacecraft entry navigation filters. This work introduces a new approach to online filtering for Martian entry by using a neural network to estimate atmospheric density and employing a consider analysis to account for the uncertainty in the estimate. The network is trained on an exponential atmospheric density model, and its parameters are dynamically adapted in real time to account for any mismatches between the true and estimated densities. The adaptation of the network is formulated as a maximum likelihood problem, leveraging the measurement innovations of the filter to identify optimal network parameters. The incorporation of a neural network enables the use of stochastic optimizers known for their efficiency in the machine learning domain within the context of the maximum likelihood approach. Performance comparisons against previous approaches are conducted in various realistic Mars entry navigation scenarios, resulting in superior estimation accuracy and precise alignment of the estimated density with a broad selection of realistic Martian atmospheres sampled from perturbed Mars-GRAM data.
Small-data Reduced Order Modeling of Chaotic Dynamics through SyCo-AE: Synthetically Constrained Autoencoders
May 14, 2023

Abstract:Data-driven reduced order modeling of chaotic dynamics can result in systems that either dissipate or diverge catastrophically. Leveraging non-linear dimensionality reduction of autoencoders and the freedom of non-linear operator inference with neural-networks, we aim to solve this problem by imposing a synthetic constraint in the reduced order space. The synthetic constraint allows our reduced order model both the freedom to remain fully non-linear and highly unstable while preventing divergence. We illustrate the methodology with the classical 40-variable Lorenz '96 equations, showing that our methodology is capable of producing medium-to-long range forecasts with lower error using less data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge