Multifidelity Ensemble Kalman Filtering Using Surrogate Models Defined by Physics-Informed Autoencoders
Paper and Code
Mar 10, 2021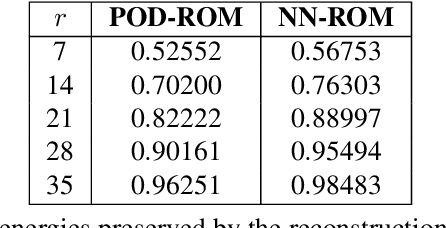
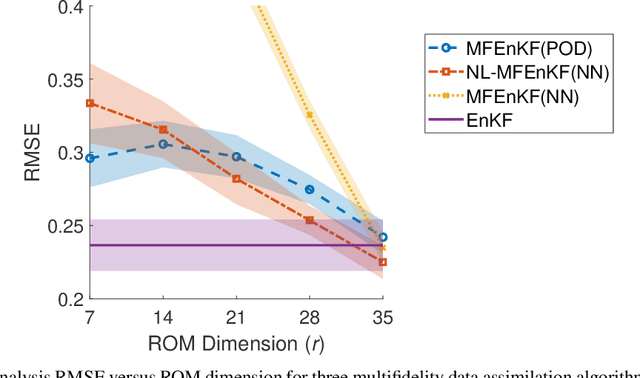
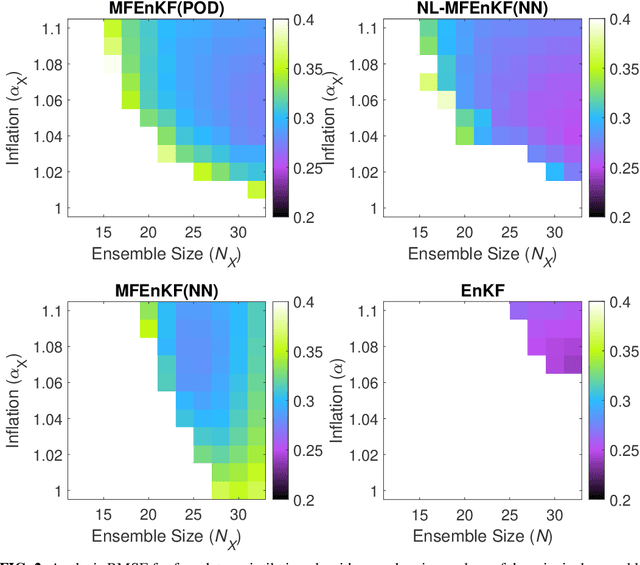
Data assimilation is a Bayesian inference process that obtains an enhanced understanding of a physical system of interest by fusing information from an inexact physics-based model, and from noisy sparse observations of reality. The multifidelity ensemble Kalman filter (MFEnKF) recently developed by the authors combines a full-order physical model and a hierarchy of reduced order surrogate models in order to increase the computational efficiency of data assimilation. The standard MFEnKF uses linear couplings between models, and is statistically optimal in case of Gaussian probability densities. This work extends MFEnKF to work with non-linear couplings between the models. Optimal nonlinear projection and interpolation operators are obtained by appropriately trained physics-informed autoencoders, and this approach allows to construct reduced order surrogate models with less error than conventional linear methods. Numerical experiments with the canonical Lorenz '96 model illustrate that nonlinear surrogates perform better than linear projection-based ones in the context of multifidelity filtering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge