Efficient Construction of Local Parametric Reduced Order Models Using Machine Learning Techniques
Paper and Code
Nov 09, 2015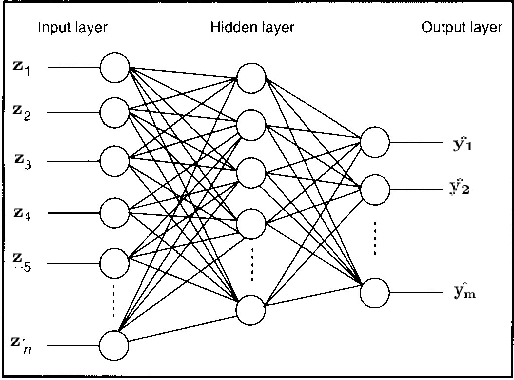
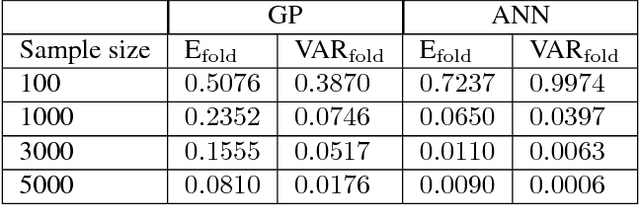
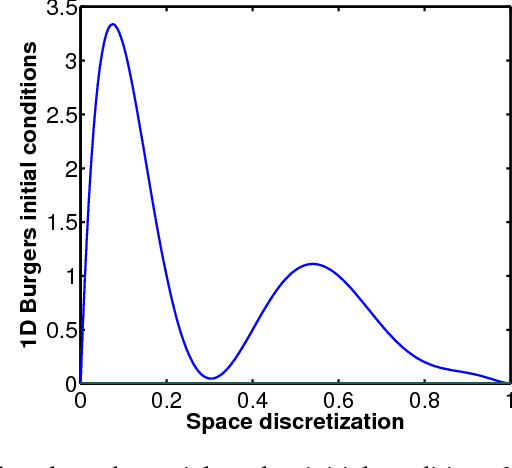
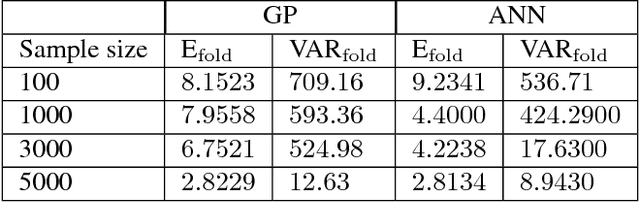
Reduced order models are computationally inexpensive approximations that capture the important dynamical characteristics of large, high-fidelity computer models of physical systems. This paper applies machine learning techniques to improve the design of parametric reduced order models. Specifically, machine learning is used to develop feasible regions in the parameter space where the admissible target accuracy is achieved with a predefined reduced order basis, to construct parametric maps, to chose the best two already existing bases for a new parameter configuration from accuracy point of view and to pre-select the optimal dimension of the reduced basis such as to meet the desired accuracy. By combining available information using bases concatenation and interpolation as well as high-fidelity solutions interpolation we are able to build accurate reduced order models associated with new parameter settings. Promising numerical results with a viscous Burgers model illustrate the potential of machine learning approaches to help design better reduced order models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge