Quantization-Guided Training for Compact TinyML Models

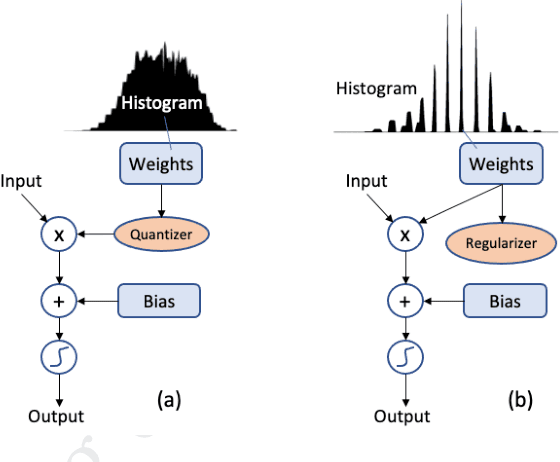
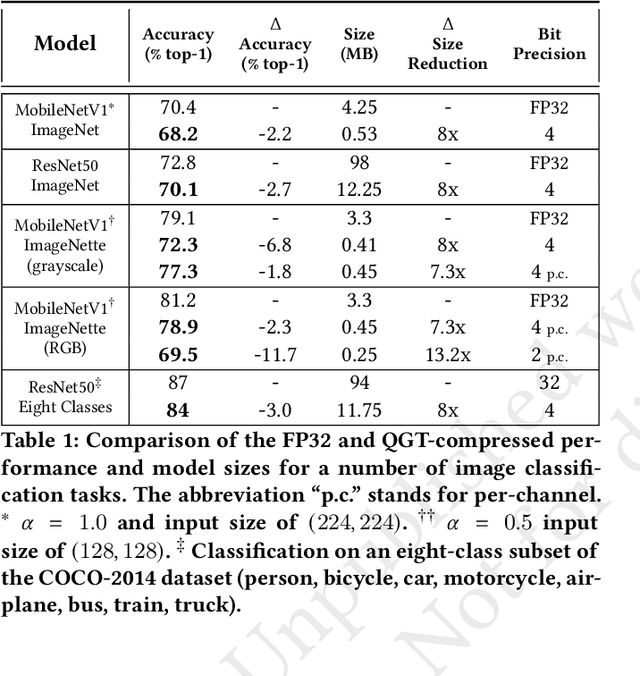
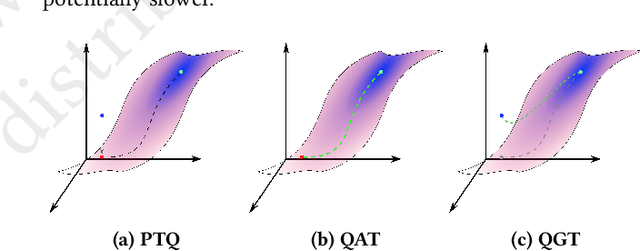
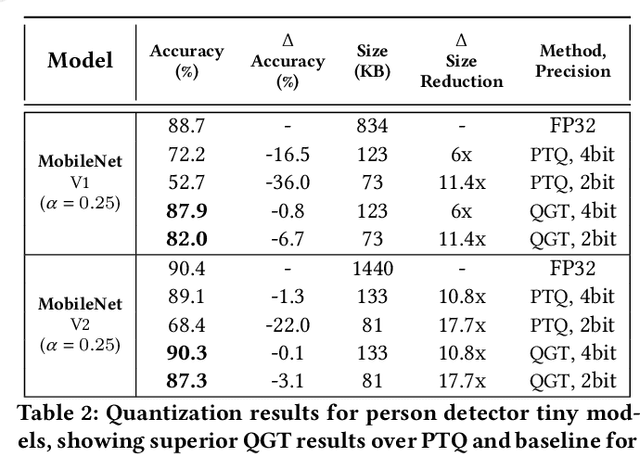
We propose a Quantization Guided Training (QGT) method to guide DNN training towards optimized low-bit-precision targets and reach extreme compression levels below 8-bit precision. Unlike standard quantization-aware training (QAT) approaches, QGT uses customized regularization to encourage weight values towards a distribution that maximizes accuracy while reducing quantization errors. One of the main benefits of this approach is the ability to identify compression bottlenecks. We validate QGT using state-of-the-art model architectures on vision datasets. We also demonstrate the effectiveness of QGT with an 81KB tiny model for person detection down to 2-bit precision (representing 17.7x size reduction), while maintaining an accuracy drop of only 3% compared to a floating-point baseline.

Subtensor Quantization for Mobilenets

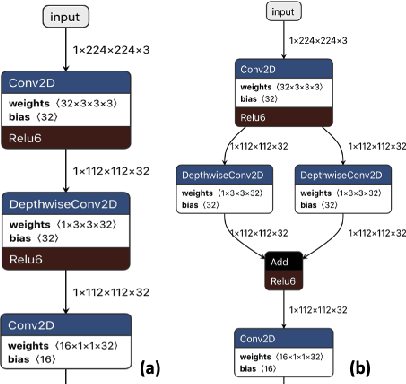
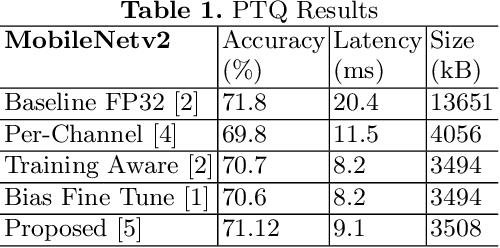
Quantization for deep neural networks (DNN) have enabled developers to deploy models with less memory and more efficient low-power inference. However, not all DNN designs are friendly to quantization. For example, the popular Mobilenet architecture has been tuned to reduce parameter size and computational latency with separable depth-wise convolutions, but not all quantization algorithms work well and the accuracy can suffer against its float point versions. In this paper, we analyzed several root causes of quantization loss and proposed alternatives that do not rely on per-channel or training-aware approaches. We evaluate the image classification task on ImageNet dataset, and our post-training quantized 8-bit inference top-1 accuracy in within 0.7% of the floating point version.

Sparsity Meets Robustness: Channel Pruning for the Feynman-Kac Formalism Principled Robust Deep Neural Nets

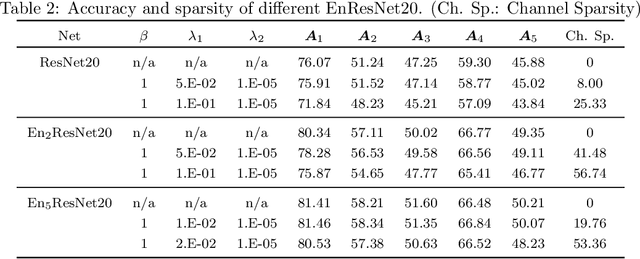
Deep neural nets (DNNs) compression is crucial for adaptation to mobile devices. Though many successful algorithms exist to compress naturally trained DNNs, developing efficient and stable compression algorithms for robustly trained DNNs remains widely open. In this paper, we focus on a co-design of efficient DNN compression algorithms and sparse neural architectures for robust and accurate deep learning. Such a co-design enables us to advance the goal of accommodating both sparsity and robustness. With this objective in mind, we leverage the relaxed augmented Lagrangian based algorithms to prune the weights of adversarially trained DNNs, at both structured and unstructured levels. Using a Feynman-Kac formalism principled robust and sparse DNNs, we can at least double the channel sparsity of the adversarially trained ResNet20 for CIFAR10 classification, meanwhile, improve the natural accuracy by $8.69$\% and the robust accuracy under the benchmark $20$ iterations of IFGSM attack by $5.42$\%. The code is available at \url{https://github.com/BaoWangMath/rvsm-rgsm-admm}.

Convergence of a Relaxed Variable Splitting Coarse Gradient Descent Method for Learning Sparse Weight Binarized Activation Neural Networks

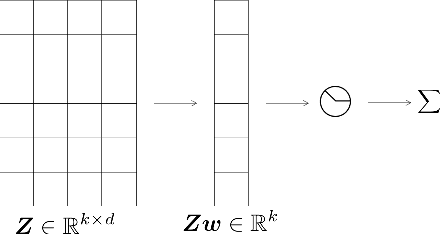
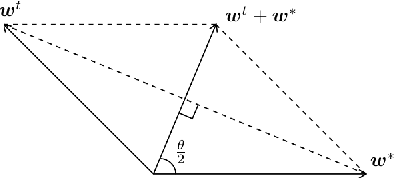
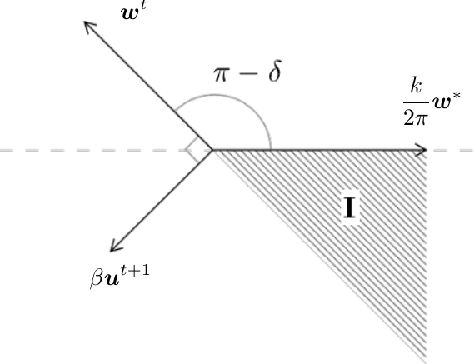
Sparsification of neural networks is one of the effective complexity reduction methods to improve efficiency and generalizability. Binarized activation offers an additional computational saving for inference. Due to vanishing gradient issue in training networks with binarized activation, coarse gradient (a.k.a. straight through estimator) is adopted in practice. In this paper, we study the problem of coarse gradient descent (CGD) learning of a one hidden layer convolutional neural network (CNN) with binarized activation function and sparse weights. It is known that when the input data is Gaussian distributed, no-overlap one hidden layer CNN with ReLU activation and general weight can be learned by GD in polynomial time at high probability in regression problems with ground truth. We propose a relaxed variable splitting method integrating thresholding and coarse gradient descent. The sparsity in network weight is realized through thresholding during the CGD training process. We prove that under threshholding of $\ell_1, \ell_0,$ and transformed-$\ell_1$ penalties, no-overlap binary activation CNN can be learned with high probability, and the iterative weights converge to a global limit which is a transformation of the true weight under a novel sparsifying operation. We found explicit error estimates of sparse weights from the true weights.