Convergence of a Relaxed Variable Splitting Coarse Gradient Descent Method for Learning Sparse Weight Binarized Activation Neural Networks
Paper and Code
Feb 09, 2019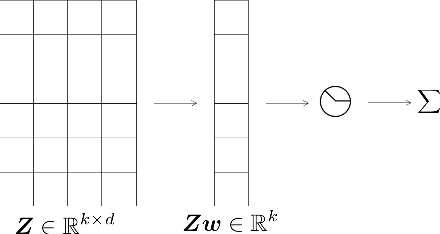

Sparsification of neural networks is one of the effective complexity reduction methods to improve efficiency and generalizability. Binarized activation offers an additional computational saving for inference. Due to vanishing gradient issue in training networks with binarized activation, coarse gradient (a.k.a. straight through estimator) is adopted in practice. In this paper, we study the problem of coarse gradient descent (CGD) learning of a one hidden layer convolutional neural network (CNN) with binarized activation function and sparse weights. It is known that when the input data is Gaussian distributed, no-overlap one hidden layer CNN with ReLU activation and general weight can be learned by GD in polynomial time at high probability in regression problems with ground truth. We propose a relaxed variable splitting method integrating thresholding and coarse gradient descent. The sparsity in network weight is realized through thresholding during the CGD training process. We prove that under threshholding of $\ell_1, \ell_0,$ and transformed-$\ell_1$ penalties, no-overlap binary activation CNN can be learned with high probability, and the iterative weights converge to a global limit which is a transformation of the true weight under a novel sparsifying operation. We found explicit error estimates of sparse weights from the true weights.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge