Bridging the Performance Gap Between Target-Free and Target-Based Reinforcement Learning With Iterated Q-Learning

In value-based reinforcement learning, removing the target network is tempting as the boostrapped target would be built from up-to-date estimates, and the spared memory occupied by the target network could be reallocated to expand the capacity of the online network. However, eliminating the target network introduces instability, leading to a decline in performance. Removing the target network also means we cannot leverage the literature developed around target networks. In this work, we propose to use a copy of the last linear layer of the online network as a target network, while sharing the remaining parameters with the up-to-date online network, hence stepping out of the binary choice between target-based and target-free methods. It enables us to leverage the concept of iterated Q-learning, which consists of learning consecutive Bellman iterations in parallel, to reduce the performance gap between target-free and target-based approaches. Our findings demonstrate that this novel method, termed iterated Shared Q-Learning (iS-QL), improves the sample efficiency of target-free approaches across various settings. Importantly, iS-QL requires a smaller memory footprint and comparable training time to classical target-based algorithms, highlighting its potential to scale reinforcement learning research.

Deep Reinforcement Learning Agents are not even close to Human Intelligence

Deep reinforcement learning (RL) agents achieve impressive results in a wide variety of tasks, but they lack zero-shot adaptation capabilities. While most robustness evaluations focus on tasks complexifications, for which human also struggle to maintain performances, no evaluation has been performed on tasks simplifications. To tackle this issue, we introduce HackAtari, a set of task variations of the Arcade Learning Environments. We use it to demonstrate that, contrary to humans, RL agents systematically exhibit huge performance drops on simpler versions of their training tasks, uncovering agents' consistent reliance on shortcuts. Our analysis across multiple algorithms and architectures highlights the persistent gap between RL agents and human behavioral intelligence, underscoring the need for new benchmarks and methodologies that enforce systematic generalization testing beyond static evaluation protocols. Training and testing in the same environment is not enough to obtain agents equipped with human-like intelligence.

Eau De $Q$-Network: Adaptive Distillation of Neural Networks in Deep Reinforcement Learning

Recent works have successfully demonstrated that sparse deep reinforcement learning agents can be competitive against their dense counterparts. This opens up opportunities for reinforcement learning applications in fields where inference time and memory requirements are cost-sensitive or limited by hardware. Until now, dense-to-sparse methods have relied on hand-designed sparsity schedules that are not synchronized with the agent's learning pace. Crucially, the final sparsity level is chosen as a hyperparameter, which requires careful tuning as setting it too high might lead to poor performances. In this work, we address these shortcomings by crafting a dense-to-sparse algorithm that we name Eau De $Q$-Network (EauDeQN). To increase sparsity at the agent's learning pace, we consider multiple online networks with different sparsity levels, where each online network is trained from a shared target network. At each target update, the online network with the smallest loss is chosen as the next target network, while the other networks are replaced by a pruned version of the chosen network. We evaluate the proposed approach on the Atari $2600$ benchmark and the MuJoCo physics simulator, showing that EauDeQN reaches high sparsity levels while keeping performances high.

Adaptive $Q$-Network: On-the-fly Target Selection for Deep Reinforcement Learning

Deep Reinforcement Learning (RL) is well known for being highly sensitive to hyperparameters, requiring practitioners substantial efforts to optimize them for the problem at hand. In recent years, the field of automated Reinforcement Learning (AutoRL) has grown in popularity by trying to address this issue. However, these approaches typically hinge on additional samples to select well-performing hyperparameters, hindering sample-efficiency and practicality in RL. Furthermore, most AutoRL methods are heavily based on already existing AutoML methods, which were originally developed neglecting the additional challenges inherent to RL due to its non-stationarities. In this work, we propose a new approach for AutoRL, called Adaptive $Q$-Network (AdaQN), that is tailored to RL to take into account the non-stationarity of the optimization procedure without requiring additional samples. AdaQN learns several $Q$-functions, each one trained with different hyperparameters, which are updated online using the $Q$-function with the smallest approximation error as a shared target. Our selection scheme simultaneously handles different hyperparameters while coping with the non-stationarity induced by the RL optimization procedure and being orthogonal to any critic-based RL algorithm. We demonstrate that AdaQN is theoretically sound and empirically validate it in MuJoCo control problems, showing benefits in sample-efficiency, overall performance, training stability, and robustness to stochasticity.

Iterated $Q$-Network: Beyond the One-Step Bellman Operator

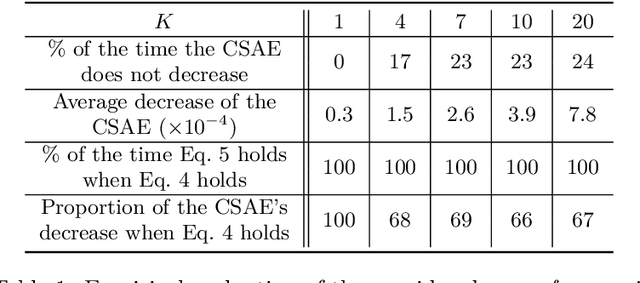
Value-based Reinforcement Learning (RL) methods rely on the application of the Bellman operator, which needs to be approximated from samples. Most approaches consist of an iterative scheme alternating the application of the Bellman operator and a subsequent projection step onto a considered function space. However, we observe that these algorithms can be improved by considering multiple iterations of the Bellman operator at once. Thus, we introduce iterated $Q$-Networks (iQN), a novel approach that learns a sequence of $Q$-function approximations where each $Q$-function serves as the target for the next one in a chain of consecutive Bellman iterations. We demonstrate that iQN is theoretically sound and show how it can be seamlessly used in value-based and actor-critic methods. We empirically demonstrate its advantages on Atari $2600$ games and in continuous-control MuJoCo environments.

Parameterized Projected Bellman Operator

Approximate value iteration~(AVI) is a family of algorithms for reinforcement learning~(RL) that aims to obtain an approximation of the optimal value function. Generally, AVI algorithms implement an iterated procedure where each step consists of (i) an application of the Bellman operator and (ii) a projection step into a considered function space. Notoriously, the Bellman operator leverages transition samples, which strongly determine its behavior, as uninformative samples can result in negligible updates or long detours, whose detrimental effects are further exacerbated by the computationally intensive projection step. To address these issues, we propose a novel alternative approach based on learning an approximate version of the Bellman operator rather than estimating it through samples as in AVI approaches. This way, we are able to (i) generalize across transition samples and (ii) avoid the computationally intensive projection step. For this reason, we call our novel operator projected Bellman operator (PBO). We formulate an optimization problem to learn PBO for generic sequential decision-making problems, and we theoretically analyze its properties in two representative classes of RL problems. Furthermore, we theoretically study our approach under the lens of AVI and devise algorithmic implementations to learn PBO in offline and online settings by leveraging neural network parameterizations. Finally, we empirically showcase the benefits of PBO w.r.t. the regular Bellman operator on several RL problems.