Relaxed Octahedral Group Convolution for Learning Symmetry Breaking in 3D Physical Systems

Deep equivariant models use symmetries to improve sample efficiency and generalization. However, the assumption of perfect symmetry in many of these models can sometimes be restrictive, especially when the data does not perfectly align with such symmetries. Thus, we introduce relaxed octahedral group convolution for modeling 3D physical systems in this paper. This flexible convolution technique provably allows the model to both maintain the highest level of equivariance that is consistent with data and discover the subtle symmetry-breaking factors in the physical systems. Empirical results validate that our approach can not only provide insights into the symmetry-breaking factors in phase transitions but also achieves superior performance in fluid super-resolution tasks.

SE-Equivariant Graph Neural Networks for Data-Efficient and Accurate Interatomic Potentials

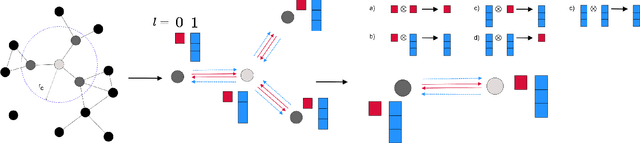
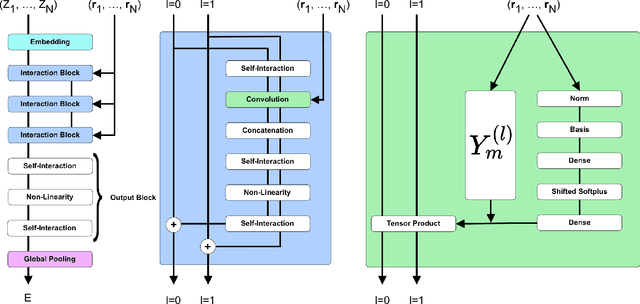
This work presents Neural Equivariant Interatomic Potentials (NequIP), a SE(3)-equivariant neural network approach for learning interatomic potentials from ab-initio calculations for molecular dynamics simulations. While most contemporary symmetry-aware models use invariant convolutions and only act on scalars, NequIP employs SE(3)-equivariant convolutions for interactions of geometric tensors, resulting in a more information-rich and faithful representation of atomic environments. The method achieves state-of-the-art accuracy on a challenging set of diverse molecules and materials while exhibiting remarkable data efficiency. NequIP outperforms existing models with up to three orders of magnitude fewer training data, challenging the widely held belief that deep neural networks require massive training sets. The high data efficiency of the method allows for the construction of accurate potentials using high-order quantum chemical level of theory as reference and enables high-fidelity molecular dynamics simulations over long time scales.

Relevance of Rotationally Equivariant Convolutions for Predicting Molecular Properties

Equivariant neural networks (ENNs) are graph neural networks embedded in $\mathbb{R}^3$ and are well suited for predicting molecular properties. The ENN library e3nn has customizable convolutions, which can be designed to depend only on distances between points, or also on angular features, making them rotationally invariant, or equivariant, respectively. This paper studies the practical value of including angular dependencies for molecular property prediction using the QM9 data set. We find that for fixed network depth, adding angular features improves the accuracy on most targets. For most, but not all, molecular properties, distance-only e3nns (L0Nets) can compensate by increasing convolutional layer depth. Our angular-feature e3nn (L1Net) architecture beats previous state-of-the-art results on the global electronic properties dipole moment, isotropic polarizability, and electronic spatial extent.

Finding Symmetry Breaking Order Parameters with Euclidean Neural Networks

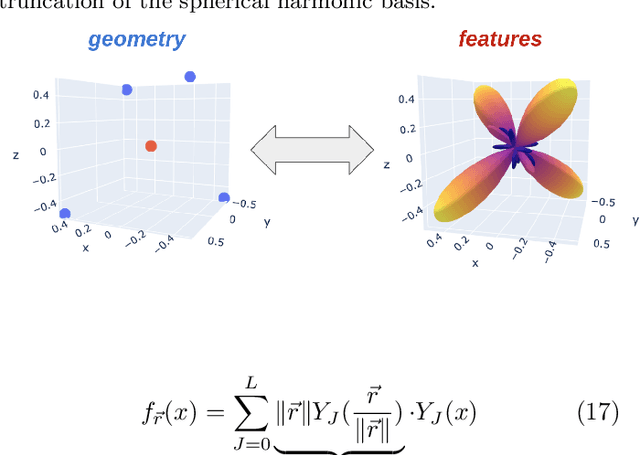
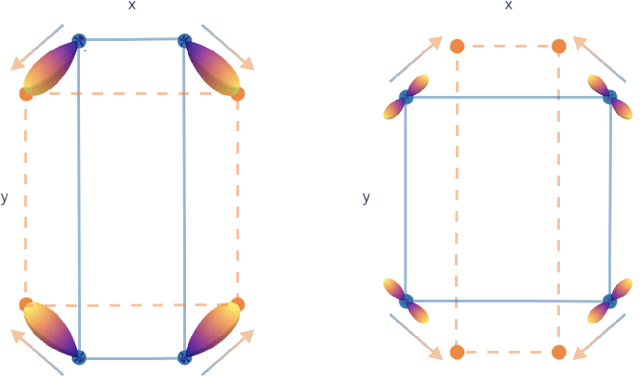
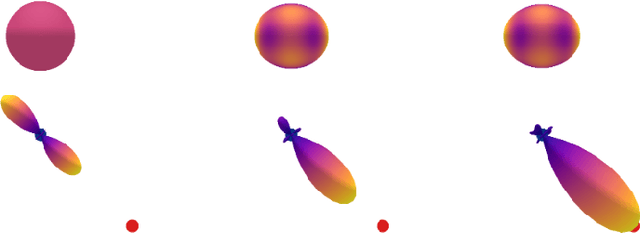
Curie's principle states that "when effects show certain asymmetry, this asymmetry must be found in the causes that gave rise to them". We demonstrate that symmetry equivariant neural networks uphold Curie's principle and this property can be used to uncover symmetry breaking order parameters necessary to make input and output data symmetrically compatible. We prove these properties mathematically and demonstrate them numerically by training a Euclidean symmetry equivariant neural network to learn symmetry breaking input to deform a square into a rectangle.