Finding Symmetry Breaking Order Parameters with Euclidean Neural Networks

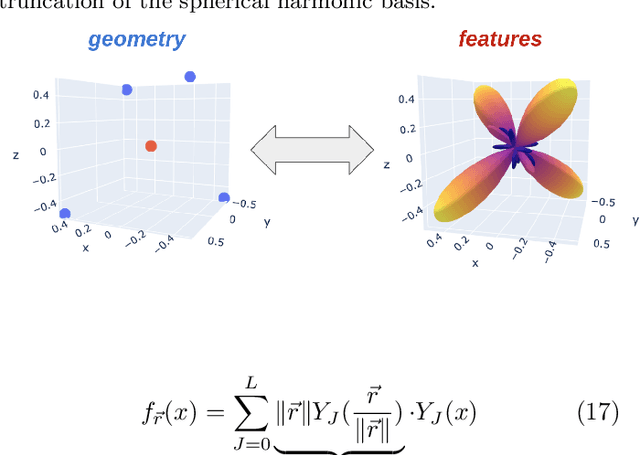
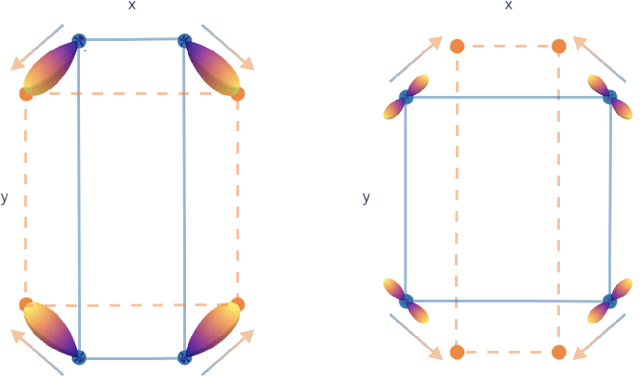
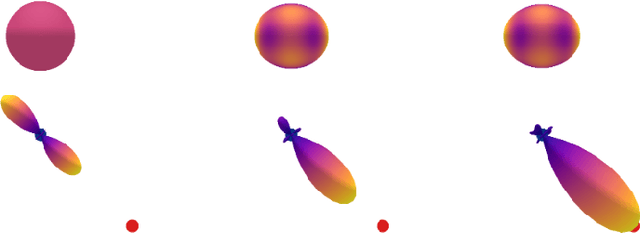
Curie's principle states that "when effects show certain asymmetry, this asymmetry must be found in the causes that gave rise to them". We demonstrate that symmetry equivariant neural networks uphold Curie's principle and this property can be used to uncover symmetry breaking order parameters necessary to make input and output data symmetrically compatible. We prove these properties mathematically and demonstrate them numerically by training a Euclidean symmetry equivariant neural network to learn symmetry breaking input to deform a square into a rectangle.