Clustering based on the In-tree Graph Structure and Affinity Propagation

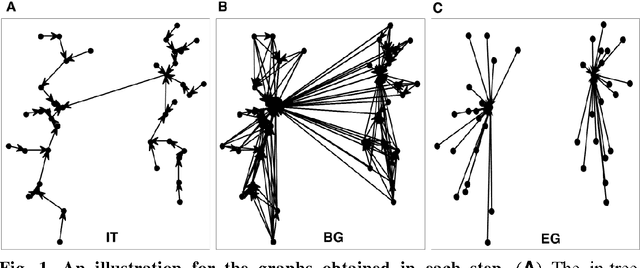
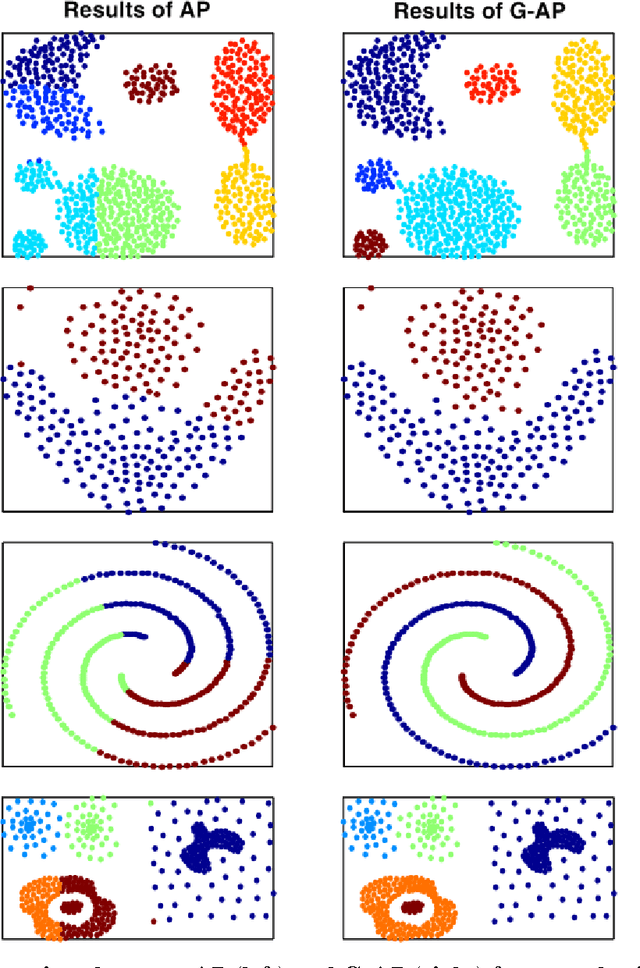
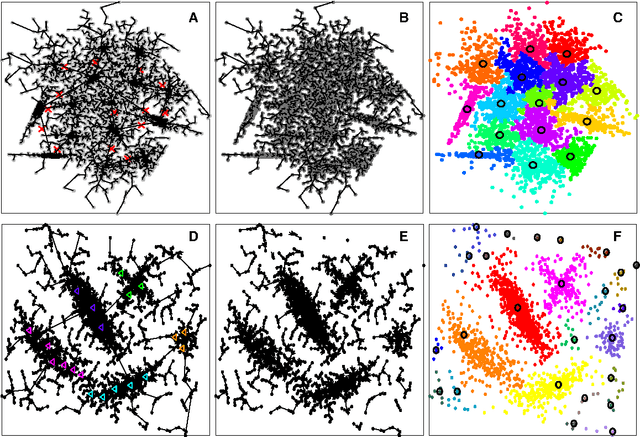
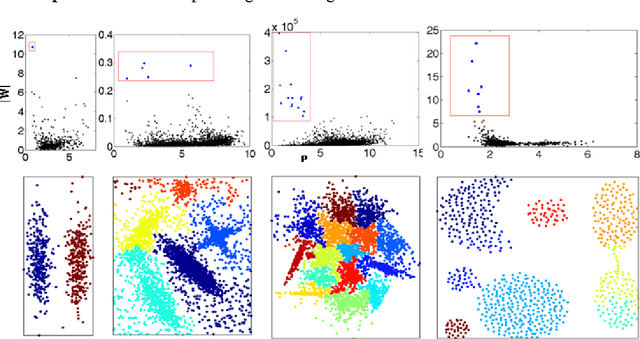
A recently proposed clustering method, called the Nearest Descent (ND), can organize the whole dataset into a sparsely connected graph, called the In-tree. This ND-based Intree structure proves able to reveal the clustering structure underlying the dataset, except one imperfect place, that is, there are some undesired edges in this In-tree which require to be removed. Here, we propose an effective way to automatically remove the undesired edges in In-tree via an effective combination of the In-tree structure with affinity propagation (AP). The key for the combination is to add edges between the reachable nodes in In-tree before using AP to remove the undesired edges. The experiments on both synthetic and real datasets demonstrate the effectiveness of the proposed method.

Nearest Descent, In-Tree, and Clustering

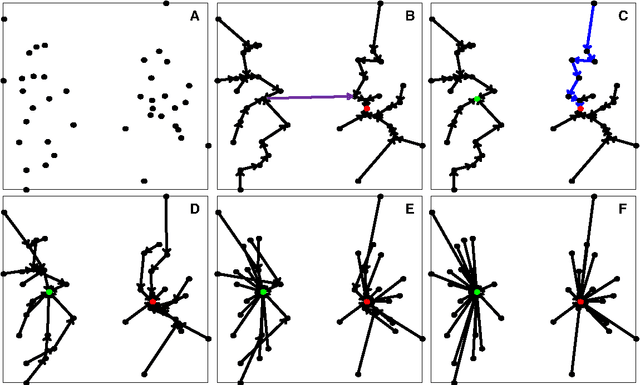
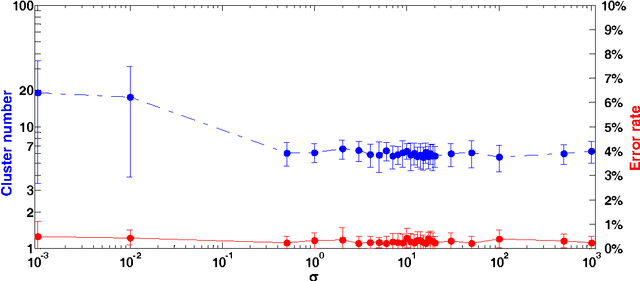
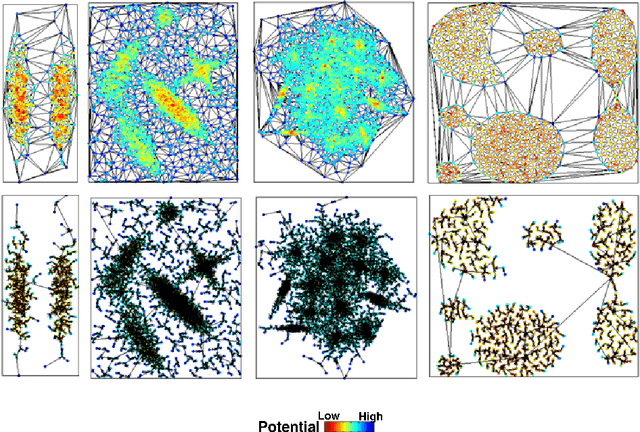
In this paper, we propose a physically inspired graph-theoretical clustering method, which first makes the data points organized into an attractive graph, called In-Tree, via a physically inspired rule, called Nearest Descent (ND). In particular, the rule of ND works to select the nearest node in the descending direction of potential as the parent node of each node, which is in essence different from the classical Gradient Descent or Steepest Descent. The constructed In-Tree proves a very good candidate for clustering due to its particular features and properties. In the In-Tree, the original clustering problem is reduced to a problem of removing a very few of undesired edges from this graph. Pleasingly, the undesired edges in In-Tree are so distinguishable that they can be easily determined in either automatic or interactive way, which is in stark contrast to the cases in the widely used Minimal Spanning Tree and k-nearest-neighbor graph. The cluster number in the proposed method can be easily determined based on some intermediate plots, and the cluster assignment for each node is easily made by quickly searching its root node in each sub-graph (also an In-Tree). The proposed method is extensively evaluated on both synthetic and real-world datasets. Overall, the proposed clustering method is a density-based one, but shows significant differences and advantages in comparison to the traditional ones. The proposed method is simple yet efficient and reliable, and is applicable to various datasets with diverse shapes, attributes and any high dimensionality

Clustering by Hierarchical Nearest Neighbor Descent (H-NND)

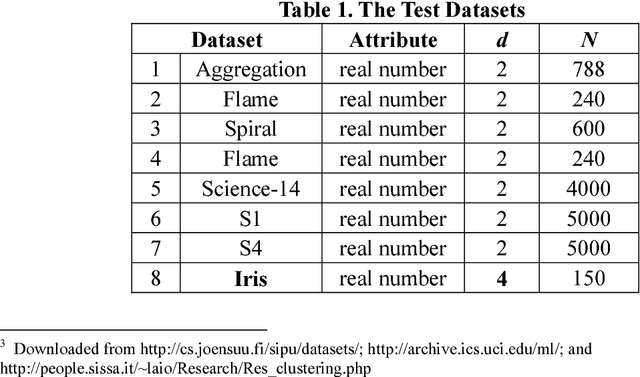
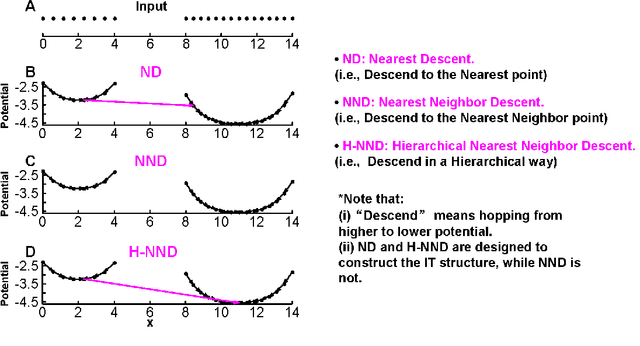
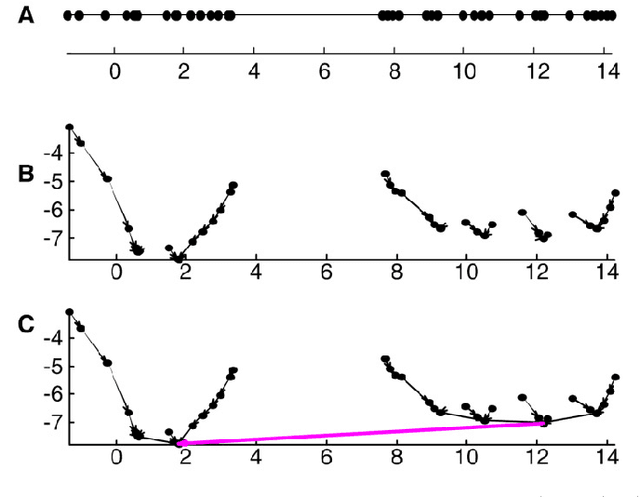
Previously in 2014, we proposed the Nearest Descent (ND) method, capable of generating an efficient Graph, called the in-tree (IT). Due to some beautiful and effective features, this IT structure proves well suited for data clustering. Although there exist some redundant edges in IT, they usually have salient features and thus it is not hard to remove them. Subsequently, in order to prevent the seemingly redundant edges from occurring, we proposed the Nearest Neighbor Descent (NND) by adding the "Neighborhood" constraint on ND. Consequently, clusters automatically emerged, without the additional requirement of removing the redundant edges. However, NND proved still not perfect, since it brought in a new yet worse problem, the "over-partitioning" problem. Now, in this paper, we propose a method, called the Hierarchical Nearest Neighbor Descent (H-NND), which overcomes the over-partitioning problem of NND via using the hierarchical strategy. Specifically, H-NND uses ND to effectively merge the over-segmented sub-graphs or clusters that NND produces. Like ND, H-NND also generates the IT structure, in which the redundant edges once again appear. This seemingly comes back to the situation that ND faces. However, compared with ND, the redundant edges in the IT structure generated by H-NND generally become more salient, thus being much easier and more reliable to be identified even by the simplest edge-removing method which takes the edge length as the only measure. In other words, the IT structure constructed by H-NND becomes more fitted for data clustering. We prove this on several clustering datasets of varying shapes, dimensions and attributes. Besides, compared with ND, H-NND generally takes less computation time to construct the IT data structure for the input data.

Clustering by Deep Nearest Neighbor Descent : A Density-based Parameter-Insensitive Clustering Method

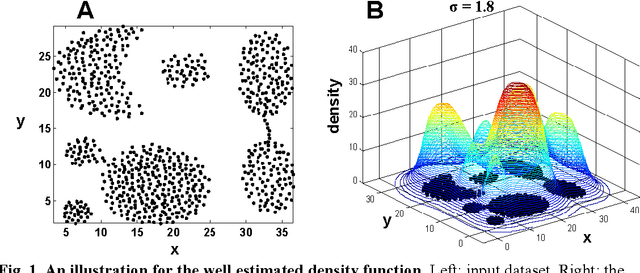
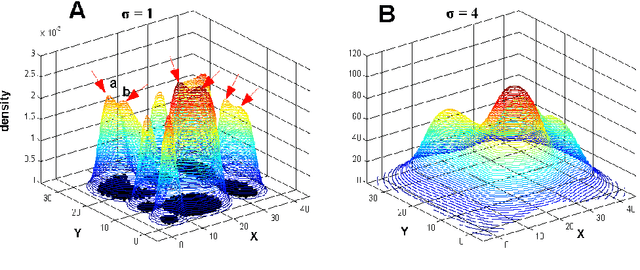
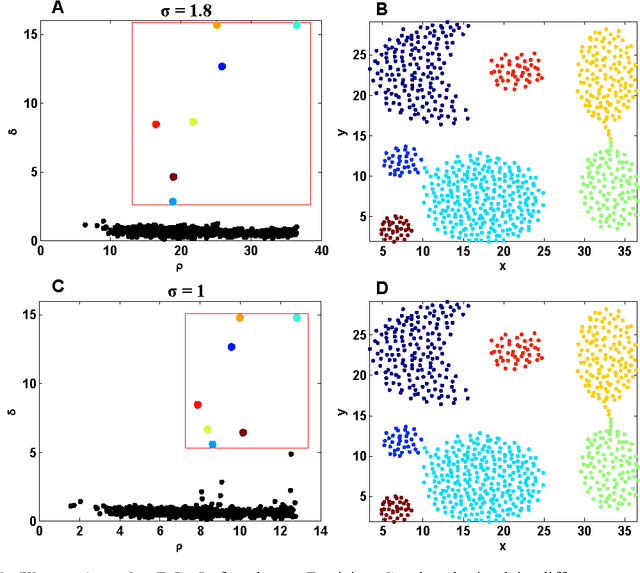
Most density-based clustering methods largely rely on how well the underlying density is estimated. However, density estimation itself is also a challenging problem, especially the determination of the kernel bandwidth. A large bandwidth could lead to the over-smoothed density estimation in which the number of density peaks could be less than the true clusters, while a small bandwidth could lead to the under-smoothed density estimation in which spurious density peaks, or called the "ripple noise", would be generated in the estimated density. In this paper, we propose a density-based hierarchical clustering method, called the Deep Nearest Neighbor Descent (D-NND), which could learn the underlying density structure layer by layer and capture the cluster structure at the same time. The over-smoothed density estimation could be largely avoided and the negative effect of the under-estimated cases could be also largely reduced. Overall, D-NND presents not only the strong capability of discovering the underlying cluster structure but also the remarkable reliability due to its insensitivity to parameters.

IT-Dendrogram: A New Member of the In-Tree Clustering Family

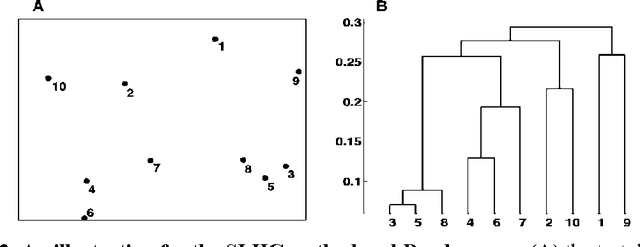
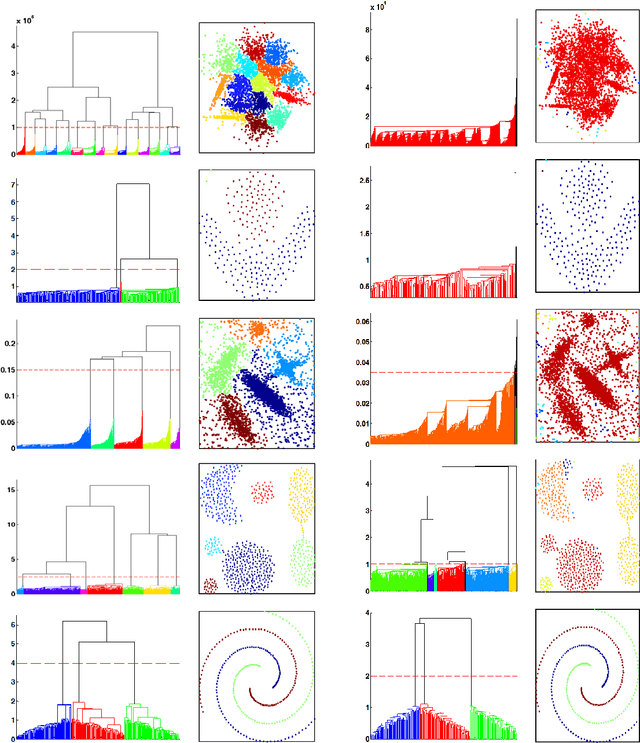
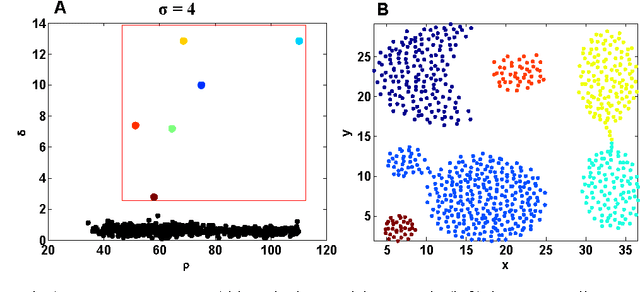
Previously, we proposed a physically-inspired method to construct data points into an effective in-tree (IT) structure, in which the underlying cluster structure in the dataset is well revealed. Although there are some edges in the IT structure requiring to be removed, such undesired edges are generally distinguishable from other edges and thus are easy to be determined. For instance, when the IT structures for the 2-dimensional (2D) datasets are graphically presented, those undesired edges can be easily spotted and interactively determined. However, in practice, there are many datasets that do not lie in the 2D Euclidean space, thus their IT structures cannot be graphically presented. But if we can effectively map those IT structures into a visualized space in which the salient features of those undesired edges are preserved, then the undesired edges in the IT structures can still be visually determined in a visualization environment. Previously, this purpose was reached by our method called IT-map. The outstanding advantage of IT-map is that clusters can still be found even with the so-called crowding problem in the embedding. In this paper, we propose another method, called IT-Dendrogram, to achieve the same goal through an effective combination of the IT structure and the single link hierarchical clustering (SLHC) method. Like IT-map, IT-Dendrogram can also effectively represent the IT structures in a visualization environment, whereas using another form, called the Dendrogram. IT-Dendrogram can serve as another visualization method to determine the undesired edges in the IT structures and thus benefit the IT-based clustering analysis. This was demonstrated on several datasets with different shapes, dimensions, and attributes. Unlike IT-map, IT-Dendrogram can always avoid the crowding problem, which could help users make more reliable cluster analysis in certain problems.

A general framework for the IT-based clustering methods

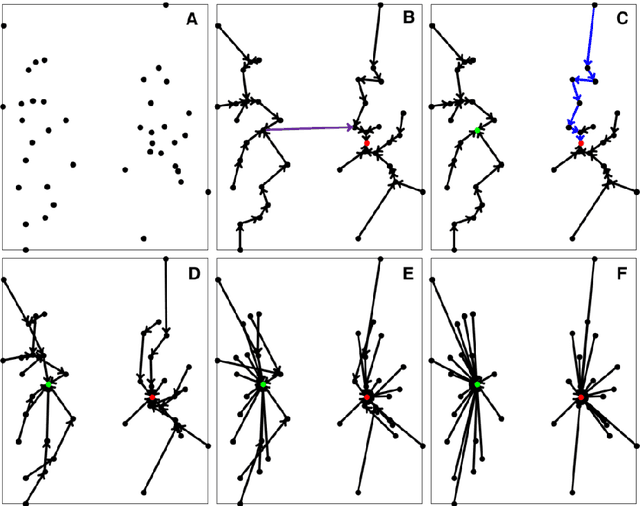
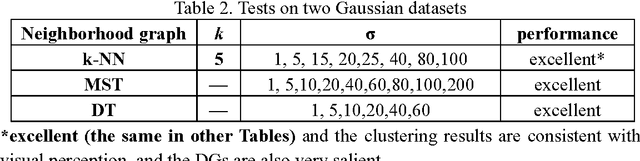
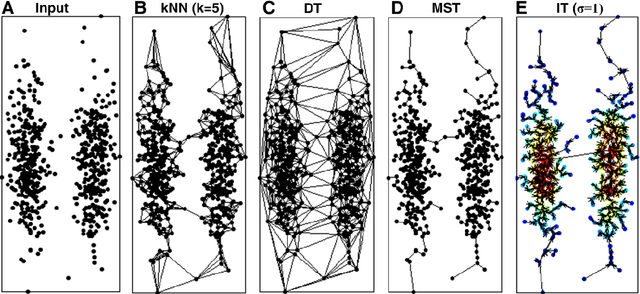
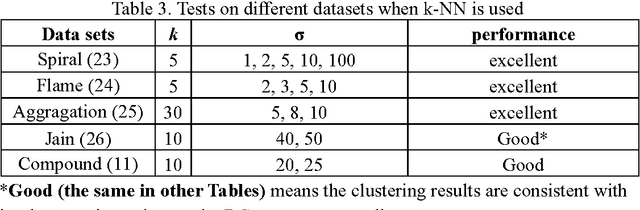
Previously, we proposed a physically inspired rule to organize the data points in a sparse yet effective structure, called the in-tree (IT) graph, which is able to capture a wide class of underlying cluster structures in the datasets, especially for the density-based datasets. Although there are some redundant edges or lines between clusters requiring to be removed by computer, this IT graph has a big advantage compared with the k-nearest-neighborhood (k-NN) or the minimal spanning tree (MST) graph, in that the redundant edges in the IT graph are much more distinguishable and thus can be easily determined by several methods previously proposed by us. In this paper, we propose a general framework to re-construct the IT graph, based on an initial neighborhood graph, such as the k-NN or MST, etc, and the corresponding graph distances. For this general framework, our previous way of constructing the IT graph turns out to be a special case of it. This general framework 1) can make the IT graph capture a wider class of underlying cluster structures in the datasets, especially for the manifolds, and 2) should be more effective to cluster the sparse or graph-based datasets.

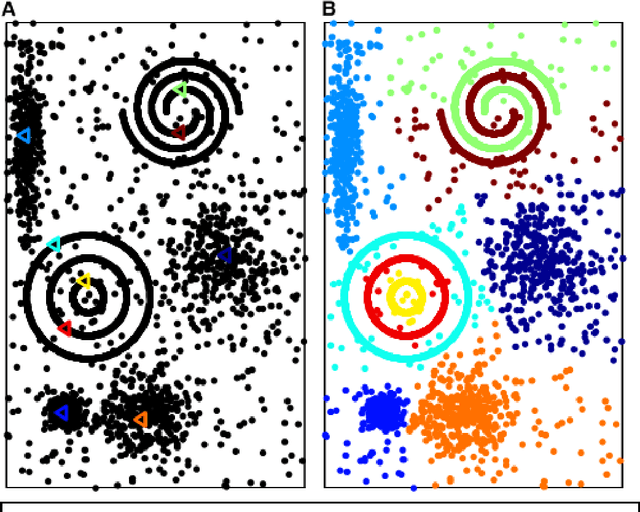
IT-map: an Effective Nonlinear Dimensionality Reduction Method for Interactive Clustering

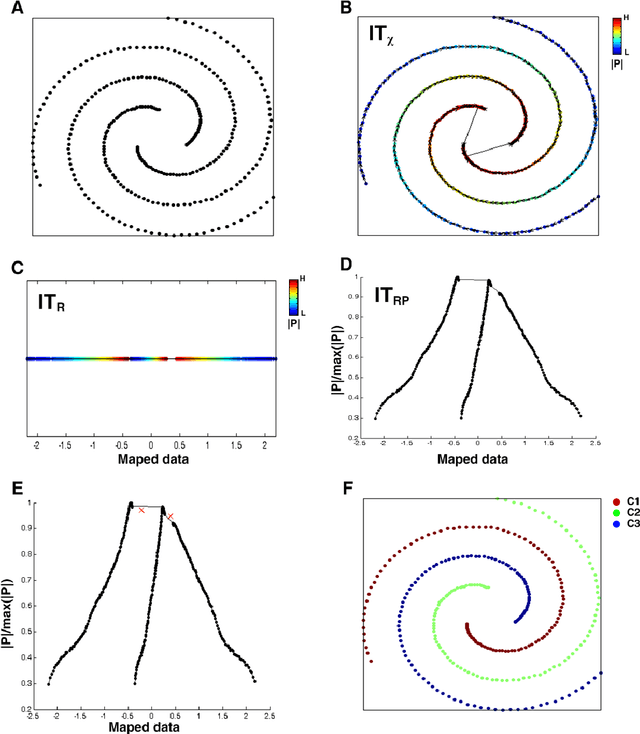
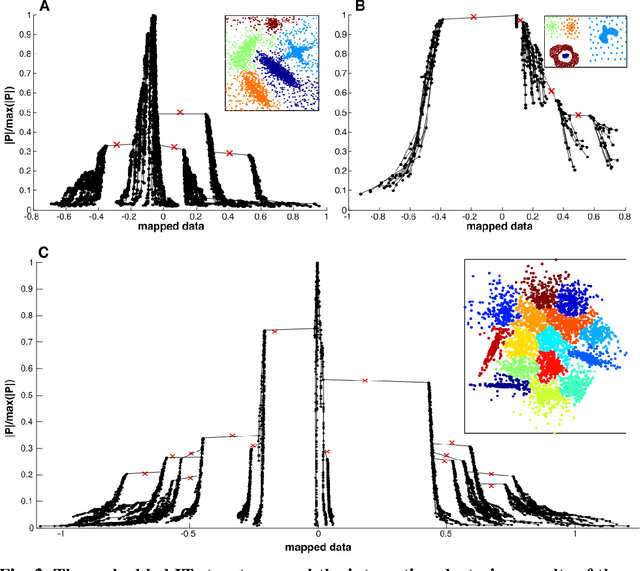
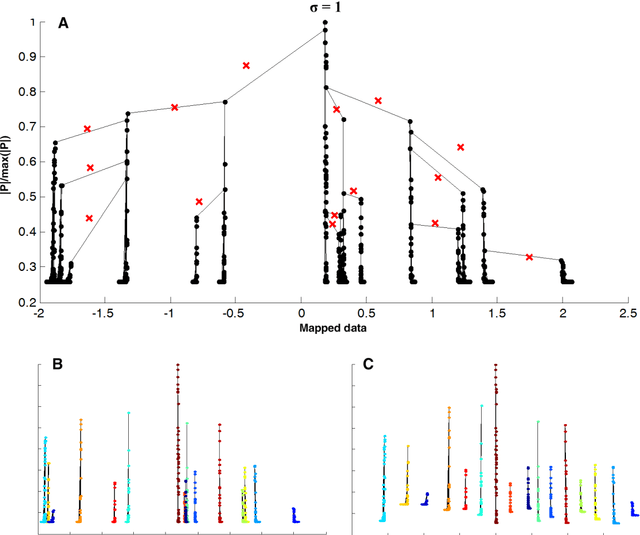
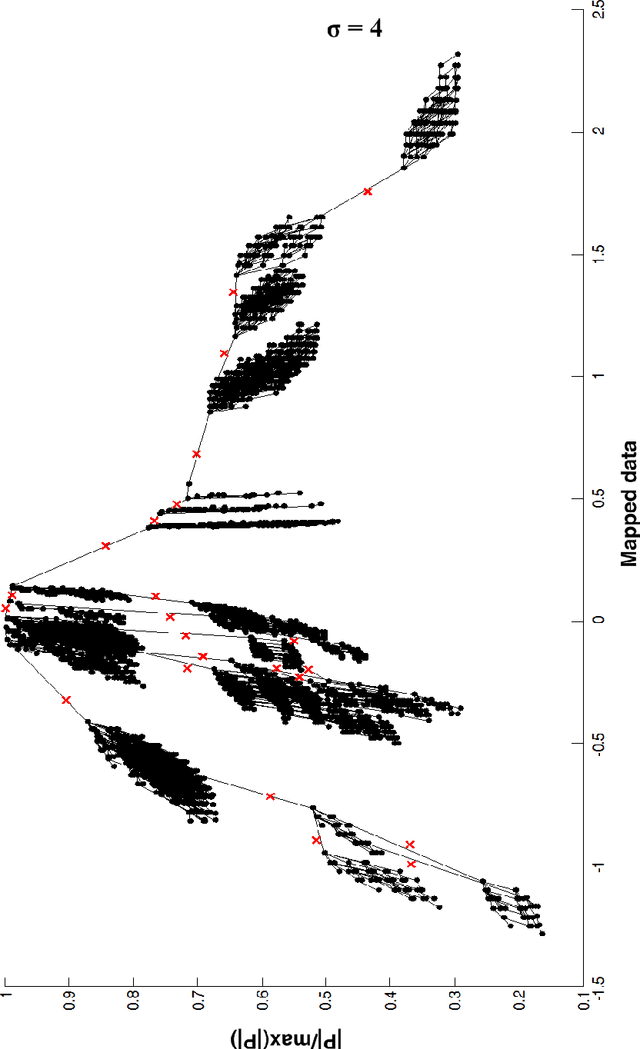
Scientists in many fields have the common and basic need of dimensionality reduction: visualizing the underlying structure of the massive multivariate data in a low-dimensional space. However, many dimensionality reduction methods confront the so-called "crowding problem" that clusters tend to overlap with each other in the embedding. Previously, researchers expect to avoid that problem and seek to make clusters maximally separated in the embedding. However, the proposed in-tree (IT) based method, called IT-map, allows clusters in the embedding to be locally overlapped, while seeking to make them distinguishable by some small yet key parts. IT-map provides a simple, effective and novel solution to cluster-preserving mapping, which makes it possible to cluster the original data points interactively and thus should be of general meaning in science and engineering.

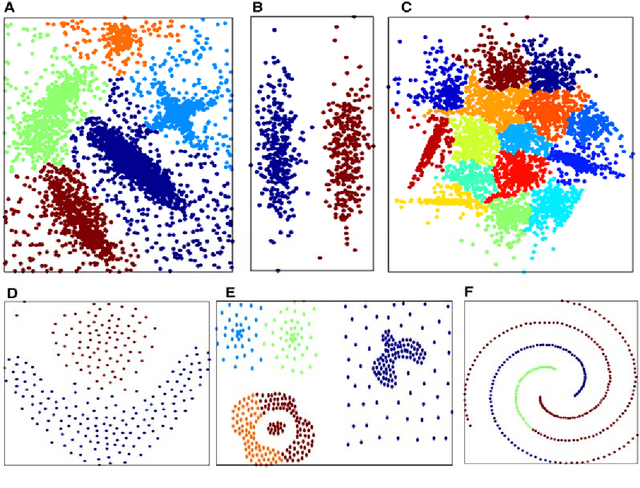
Nonparametric Nearest Neighbor Descent Clustering based on Delaunay Triangulation

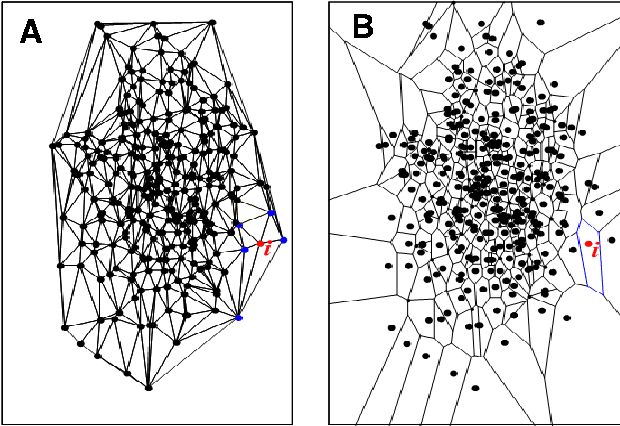
In our physically inspired in-tree (IT) based clustering algorithm and the series after it, there is only one free parameter involved in computing the potential value of each point. In this work, based on the Delaunay Triangulation or its dual Voronoi tessellation, we propose a nonparametric process to compute potential values by the local information. This computation, though nonparametric, is relatively very rough, and consequently, many local extreme points will be generated. However, unlike those gradient-based methods, our IT-based methods are generally insensitive to those local extremes. This positively demonstrates the superiority of these parametric (previous) and nonparametric (in this work) IT-based methods.

Clustering by Descending to the Nearest Neighbor in the Delaunay Graph Space

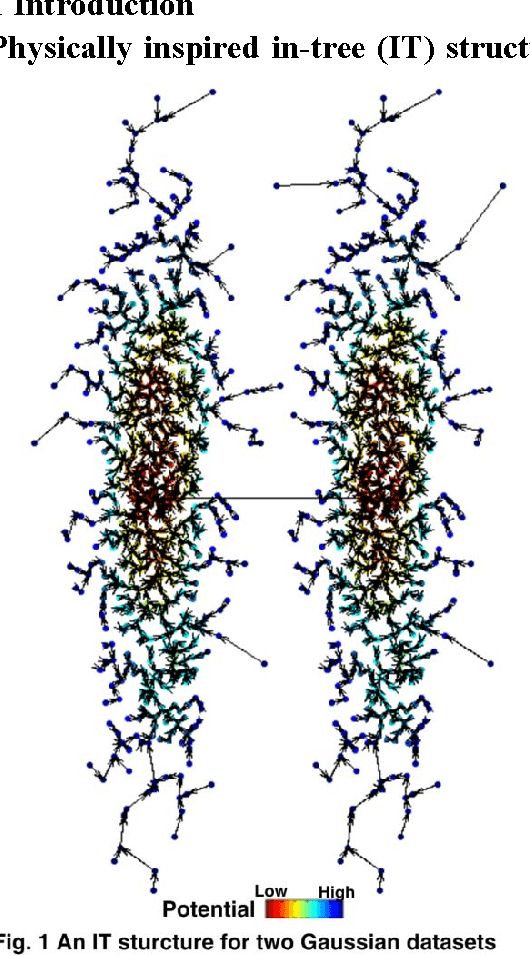
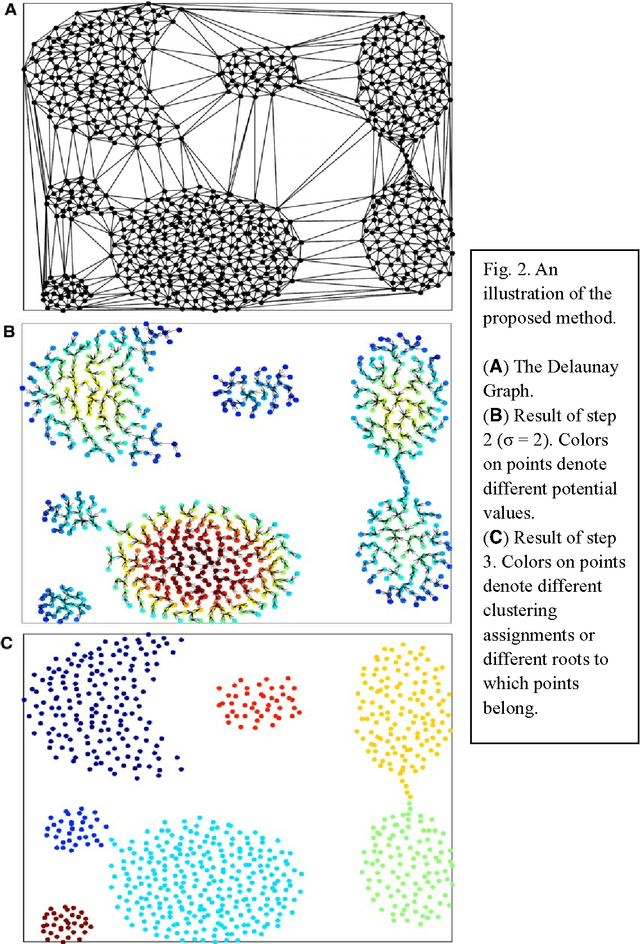
In our previous works, we proposed a physically-inspired rule to organize the data points into an in-tree (IT) structure, in which some undesired edges are allowed to occur. By removing those undesired or redundant edges, this IT structure is divided into several separate parts, each representing one cluster. In this work, we seek to prevent the undesired edges from arising at the source. Before using the physically-inspired rule, data points are at first organized into a proximity graph which restricts each point to select the optimal directed neighbor just among its neighbors. Consequently, separated in-trees or clusters automatically arise, without redundant edges requiring to be removed.

An Effective Semi-supervised Divisive Clustering Algorithm

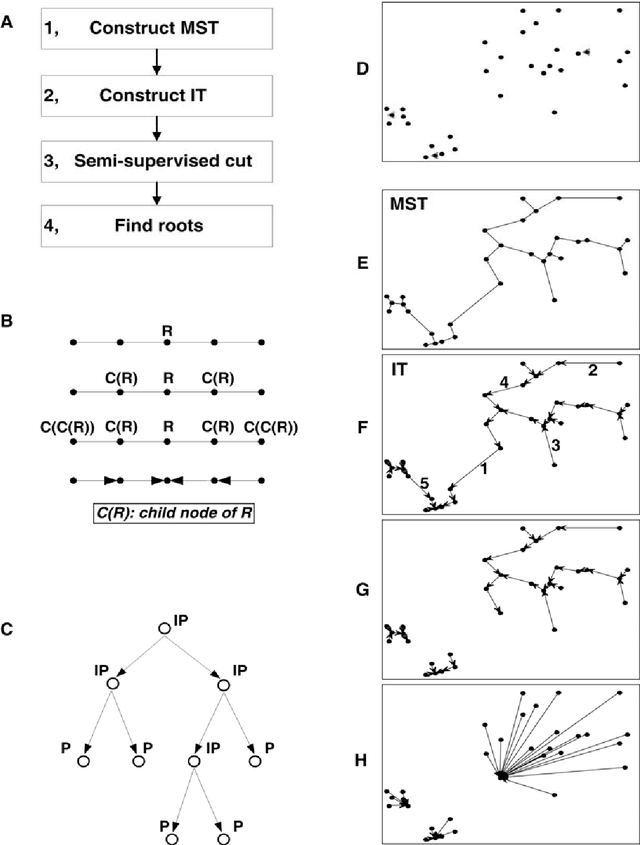
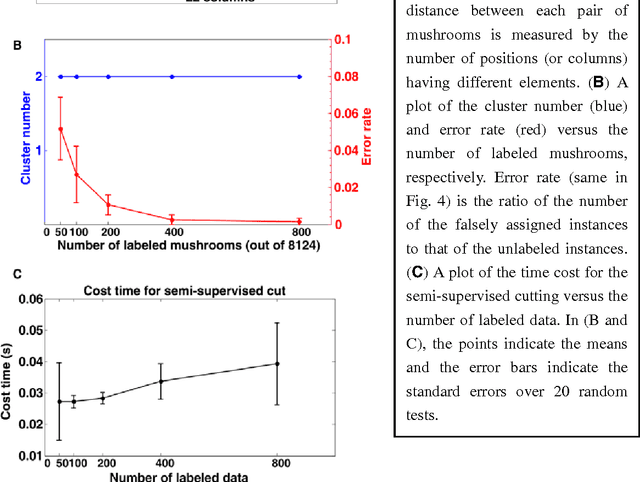
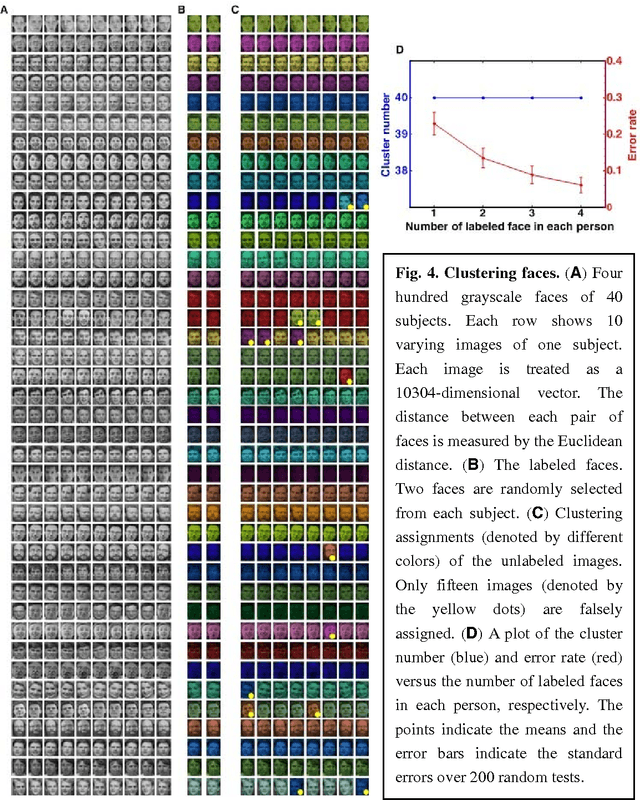
Nowadays, data are generated massively and rapidly from scientific fields as bioinformatics, neuroscience and astronomy to business and engineering fields. Cluster analysis, as one of the major data analysis tools, is therefore more significant than ever. We propose in this work an effective Semi-supervised Divisive Clustering algorithm (SDC). Data points are first organized by a minimal spanning tree. Next, this tree structure is transitioned to the in-tree structure, and then divided into sub-trees under the supervision of the labeled data, and in the end, all points in the sub-trees are directly associated with specific cluster centers. SDC is fully automatic, non-iterative, involving no free parameter, insensitive to noise, able to detect irregularly shaped cluster structures, applicable to the data sets of high dimensionality and different attributes. The power of SDC is demonstrated on several datasets.