Nearest Descent, In-Tree, and Clustering
Paper and Code
Jan 25, 2018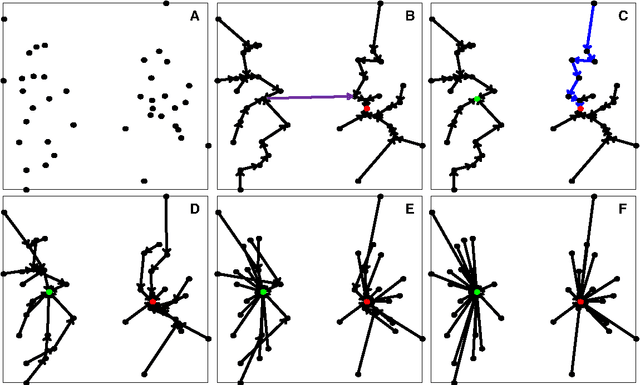
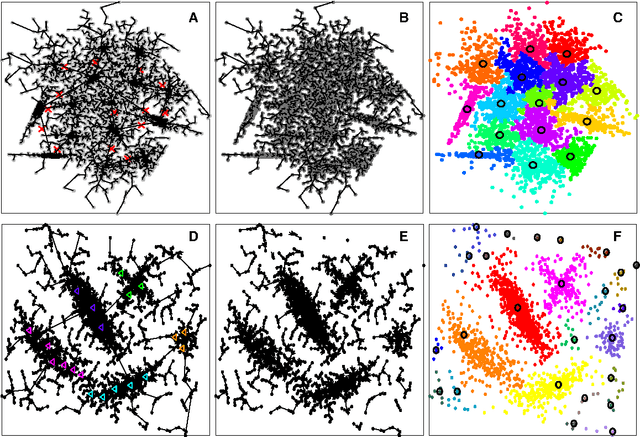
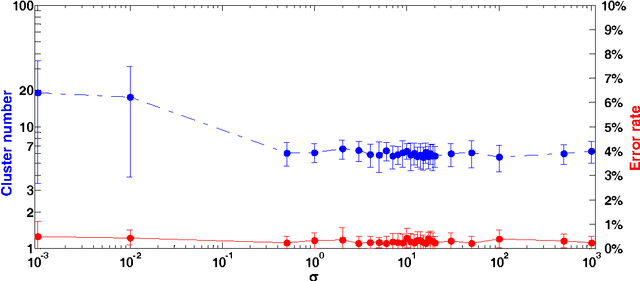

In this paper, we propose a physically inspired graph-theoretical clustering method, which first makes the data points organized into an attractive graph, called In-Tree, via a physically inspired rule, called Nearest Descent (ND). In particular, the rule of ND works to select the nearest node in the descending direction of potential as the parent node of each node, which is in essence different from the classical Gradient Descent or Steepest Descent. The constructed In-Tree proves a very good candidate for clustering due to its particular features and properties. In the In-Tree, the original clustering problem is reduced to a problem of removing a very few of undesired edges from this graph. Pleasingly, the undesired edges in In-Tree are so distinguishable that they can be easily determined in either automatic or interactive way, which is in stark contrast to the cases in the widely used Minimal Spanning Tree and k-nearest-neighbor graph. The cluster number in the proposed method can be easily determined based on some intermediate plots, and the cluster assignment for each node is easily made by quickly searching its root node in each sub-graph (also an In-Tree). The proposed method is extensively evaluated on both synthetic and real-world datasets. Overall, the proposed clustering method is a density-based one, but shows significant differences and advantages in comparison to the traditional ones. The proposed method is simple yet efficient and reliable, and is applicable to various datasets with diverse shapes, attributes and any high dimensionality
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge