Nonparametric Nearest Neighbor Descent Clustering based on Delaunay Triangulation
Paper and Code
Mar 18, 2015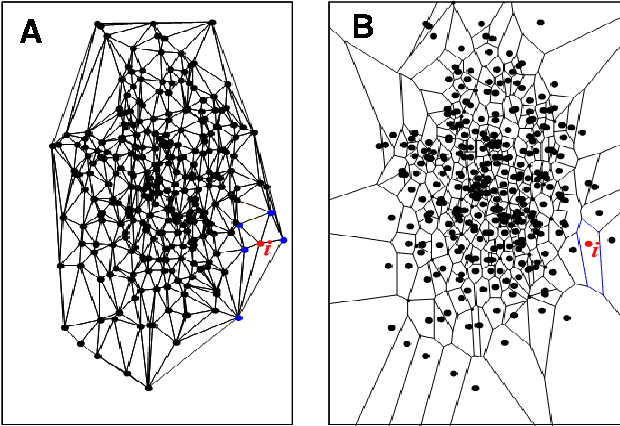
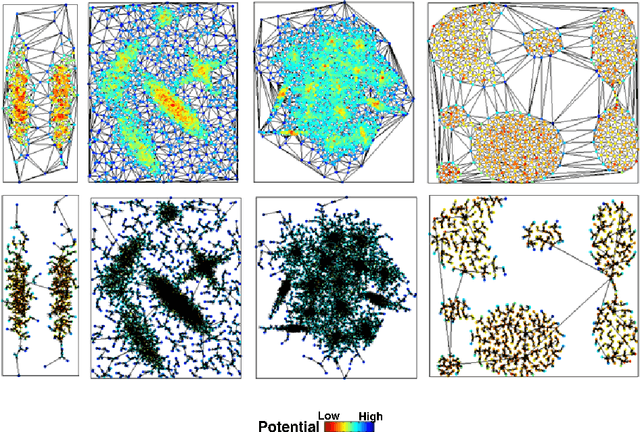

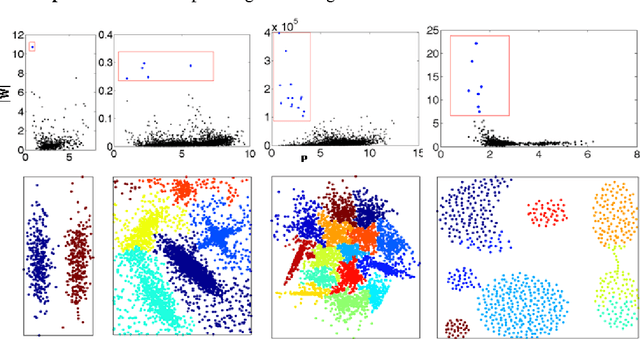
In our physically inspired in-tree (IT) based clustering algorithm and the series after it, there is only one free parameter involved in computing the potential value of each point. In this work, based on the Delaunay Triangulation or its dual Voronoi tessellation, we propose a nonparametric process to compute potential values by the local information. This computation, though nonparametric, is relatively very rough, and consequently, many local extreme points will be generated. However, unlike those gradient-based methods, our IT-based methods are generally insensitive to those local extremes. This positively demonstrates the superiority of these parametric (previous) and nonparametric (in this work) IT-based methods.
* 7 pages; 6 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge