A Unified Approach to Inferring Chemical Compounds with the Desired Aqueous Solubility

Aqueous solubility (AS) is a key physiochemical property that plays a crucial role in drug discovery and material design. We report a novel unified approach to predict and infer chemical compounds with the desired AS based on simple deterministic graph-theoretic descriptors, multiple linear regression (MLR) and mixed integer linear programming (MILP). Selected descriptors based on a forward stepwise procedure enabled the simplest regression model, MLR, to achieve significantly good prediction accuracy compared to the existing approaches, achieving the accuracy in the range [0.7191, 0.9377] for 29 diverse datasets. By simulating these descriptors and learning models as MILPs, we inferred mathematically exact and optimal compounds with the desired AS, prescribed structures, and up to 50 non-hydrogen atoms in a reasonable time range [6, 1204] seconds. These findings indicate a strong correlation between the simple graph-theoretic descriptors and the AS of compounds, potentially leading to a deeper understanding of their AS without relying on widely used complicated chemical descriptors and complex machine learning models that are computationally expensive, and therefore difficult to use for inference. An implementation of the proposed approach is available at https://github.com/ku-dml/mol-infer/tree/master/AqSol.

Cycle-Configuration: A Novel Graph-theoretic Descriptor Set for Molecular Inference

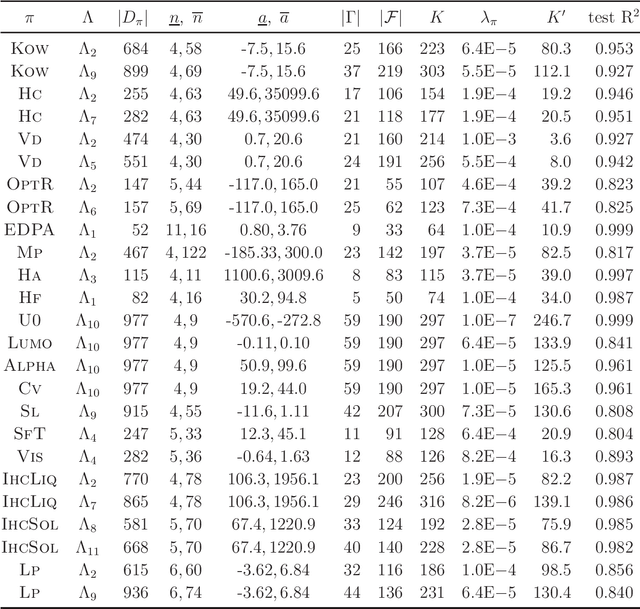
In this paper, we propose a novel family of descriptors of chemical graphs, named cycle-configuration (CC), that can be used in the standard "two-layered (2L) model" of mol-infer, a molecular inference framework based on mixed integer linear programming (MILP) and machine learning (ML). Proposed descriptors capture the notion of ortho/meta/para patterns that appear in aromatic rings, which has been impossible in the framework so far. Computational experiments show that, when the new descriptors are supplied, we can construct prediction functions of similar or better performance for all of the 27 tested chemical properties. We also provide an MILP formulation that asks for a chemical graph with desired properties under the 2L model with CC descriptors (2L+CC model). We show that a chemical graph with up to 50 non-hydrogen vertices can be inferred in a practical time.

On the Trade-off between the Number of Nodes and the Number of Trees in a Random Forest

In this paper, we focus on the prediction phase of a random forest and study the problem of representing a bag of decision trees using a smaller bag of decision trees, where we only consider binary decision problems on the binary domain and simple decision trees in which an internal node is limited to querying the Boolean value of a single variable. As a main result, we show that the majority function of $n$ variables can be represented by a bag of $T$ ($< n$) decision trees each with polynomial size if $n-T$ is a constant, where $n$ and $T$ must be odd (in order to avoid the tie break). We also show that a bag of $n$ decision trees can be represented by a bag of $T$ decision trees each with polynomial size if $n-T$ is a constant and a small classification error is allowed. A related result on the $k$-out-of-$n$ functions is presented too.

Molecular Design Based on Integer Programming and Splitting Data Sets by Hyperplanes

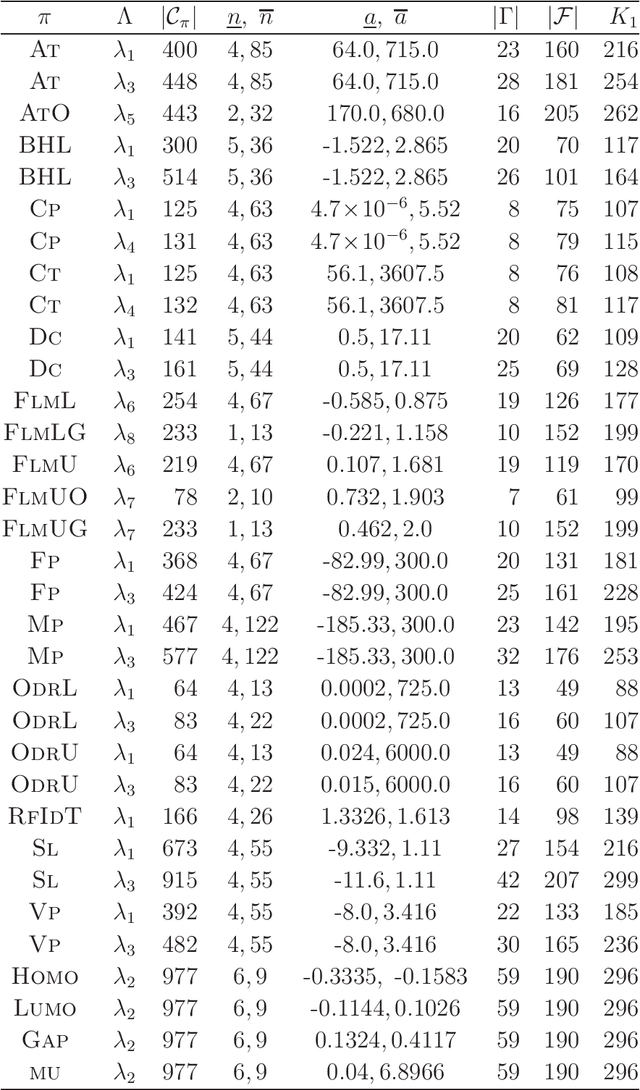
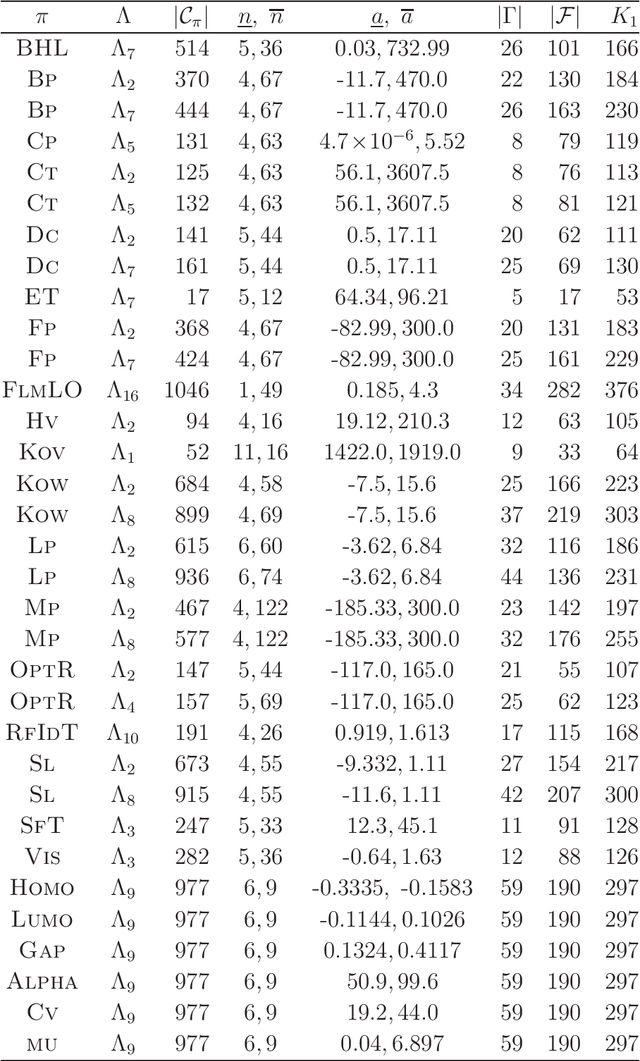
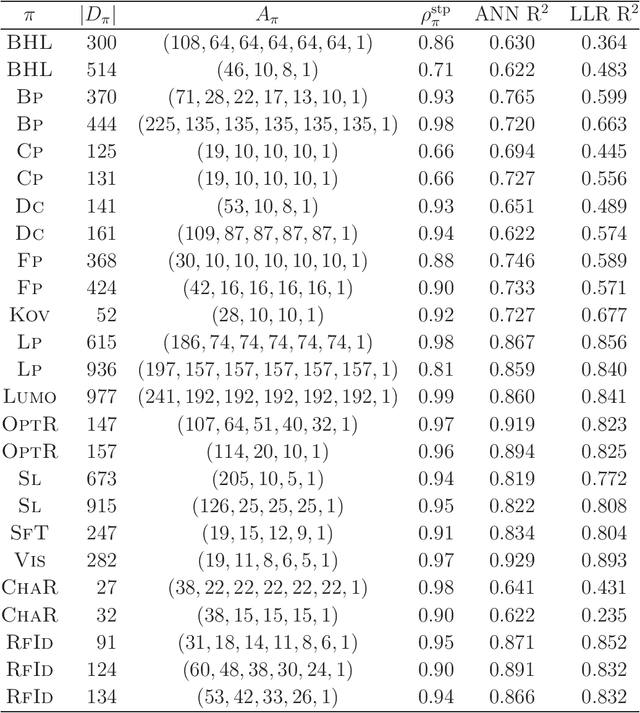
A novel framework for designing the molecular structure of chemical compounds with a desired chemical property has recently been proposed. The framework infers a desired chemical graph by solving a mixed integer linear program (MILP) that simulates the computation process of a feature function defined by a two-layered model on chemical graphs and a prediction function constructed by a machine learning method. To improve the learning performance of prediction functions in the framework, we design a method that splits a given data set $\mathcal{C}$ into two subsets $\mathcal{C}^{(i)},i=1,2$ by a hyperplane in a chemical space so that most compounds in the first (resp., second) subset have observed values lower (resp., higher) than a threshold $\theta$. We construct a prediction function $\psi$ to the data set $\mathcal{C}$ by combining prediction functions $\psi_i,i=1,2$ each of which is constructed on $\mathcal{C}^{(i)}$ independently. The results of our computational experiments suggest that the proposed method improved the learning performance for several chemical properties to which a good prediction function has been difficult to construct.

Molecular Design Based on Integer Programming and Quadratic Descriptors in a Two-layered Model

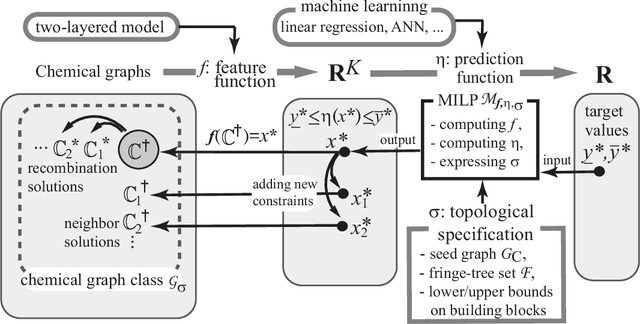
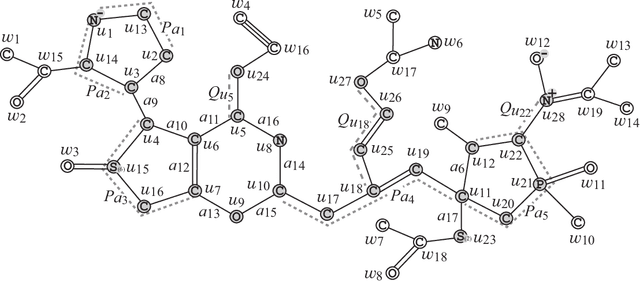
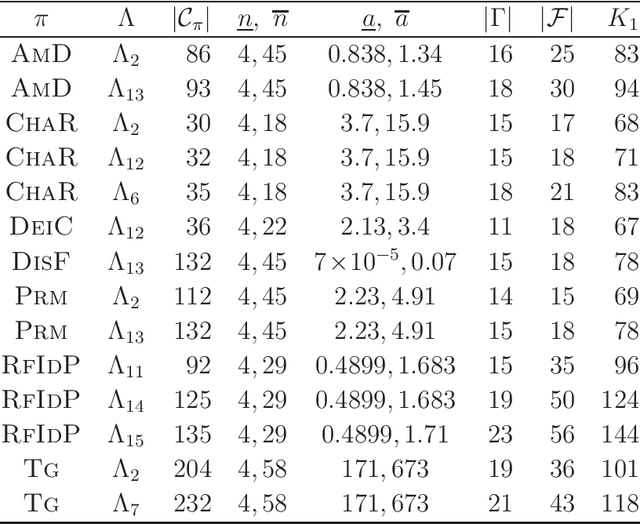
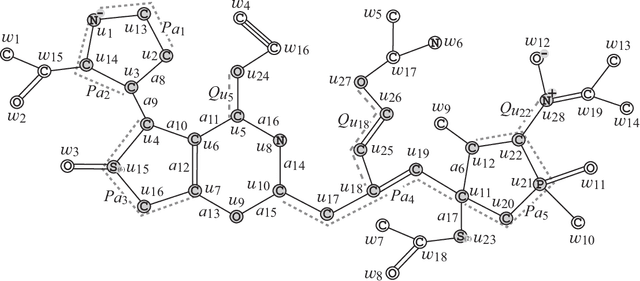
A novel framework has recently been proposed for designing the molecular structure of chemical compounds with a desired chemical property, where design of novel drugs is an important topic in bioinformatics and chemo-informatics. The framework infers a desired chemical graph by solving a mixed integer linear program (MILP) that simulates the computation process of a feature function defined by a two-layered model on chemical graphs and a prediction function constructed by a machine learning method. A set of graph theoretical descriptors in the feature function plays a key role to derive a compact formulation of such an MILP. To improve the learning performance of prediction functions in the framework maintaining the compactness of the MILP, this paper utilizes the product of two of those descriptors as a new descriptor and then designs a method of reducing the number of descriptors. The results of our computational experiments suggest that the proposed method improved the learning performance for many chemical properties and can infer a chemical structure with up to 50 non-hydrogen atoms.

On the Size and Width of the Decoder of a Boolean Threshold Autoencoder

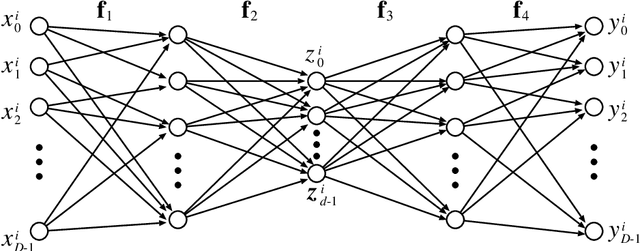
In this paper, we study the size and width of autoencoders consisting of Boolean threshold functions, where an autoencoder is a layered neural network whose structure can be viewed as consisting of an encoder, which compresses an input vector to a lower dimensional vector, and a decoder which transforms the low-dimensional vector back to the original input vector exactly (or approximately). We focus on the decoder part, and show that $\Omega(\sqrt{Dn/d})$ and $O(\sqrt{Dn})$ nodes are required to transform $n$ vectors in $d$-dimensional binary space to $D$-dimensional binary space. We also show that the width can be reduced if we allow small errors, where the error is defined as the average of the Hamming distance between each vector input to the encoder part and the resulting vector output by the decoder.

A Method for Inferring Polymers Based on Linear Regression and Integer Programming

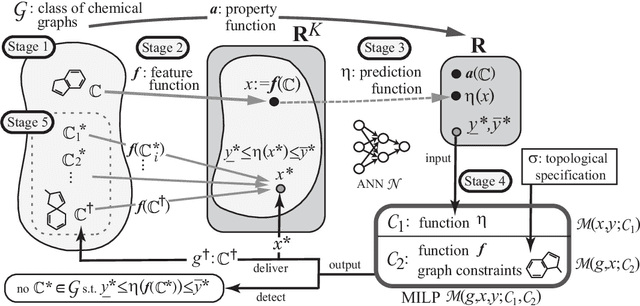
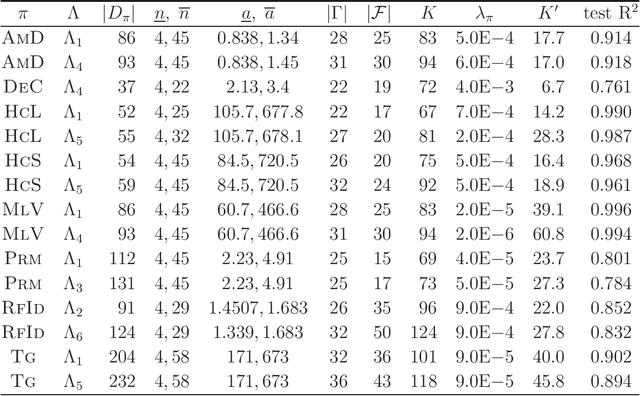
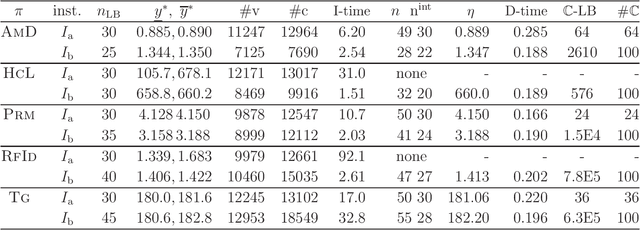
A novel framework has recently been proposed for designing the molecular structure of chemical compounds with a desired chemical property using both artificial neural networks and mixed integer linear programming. In this paper, we design a new method for inferring a polymer based on the framework. For this, we introduce a new way of representing a polymer as a form of monomer and define new descriptors that feature the structure of polymers. We also use linear regression as a building block of constructing a prediction function in the framework. The results of our computational experiments reveal a set of chemical properties on polymers to which a prediction function constructed with linear regression performs well. We also observe that the proposed method can infer polymers with up to 50 non-hydrogen atoms in a monomer form.

Molecular Design Based on Artificial Neural Networks, Integer Programming and Grid Neighbor Search

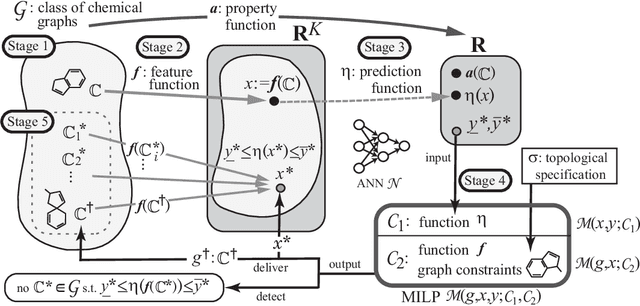
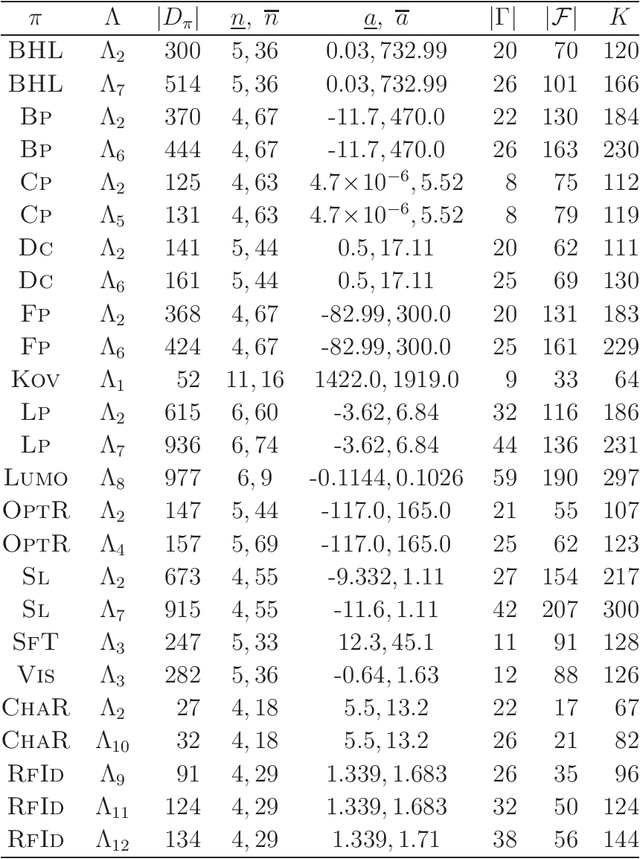
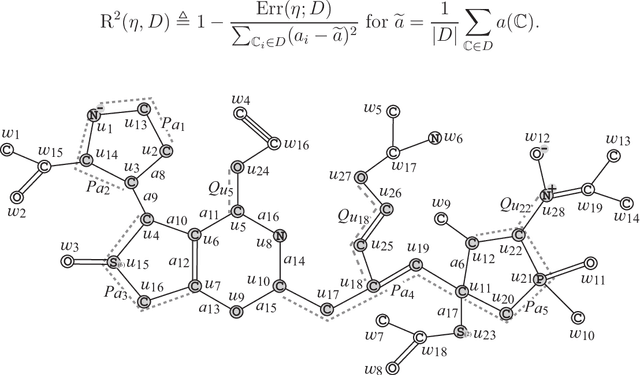
A novel framework has recently been proposed for designing the molecular structure of chemical compounds with a desired chemical property using both artificial neural networks and mixed integer linear programming. In the framework, a chemical graph with a target chemical value is inferred as a feasible solution of a mixed integer linear program that represents a prediction function and other requirements on the structure of graphs. In this paper, we propose a procedure for generating other feasible solutions of the mixed integer linear program by searching the neighbor of output chemical graph in a search space. The procedure is combined in the framework as a new building block. The results of our computational experiments suggest that the proposed method can generate an additional number of new chemical graphs with up to 50 non-hydrogen atoms.

An Inverse QSAR Method Based on Linear Regression and Integer Programming

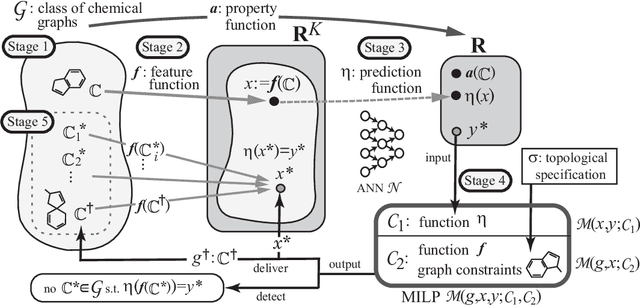
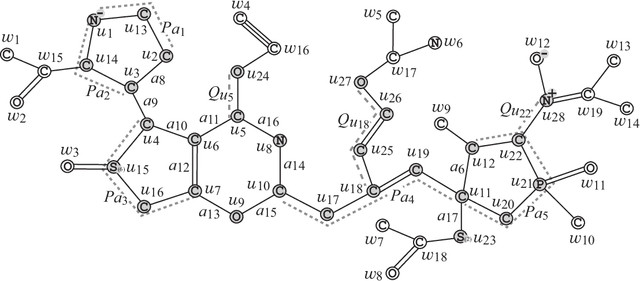
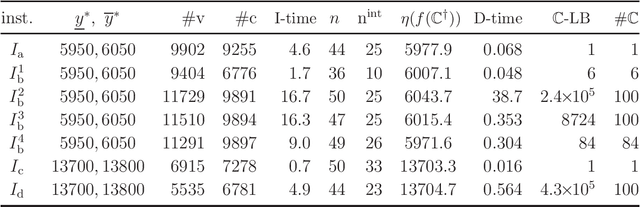
Recently a novel framework has been proposed for designing the molecular structure of chemical compounds using both artificial neural networks (ANNs) and mixed integer linear programming (MILP). In the framework, we first define a feature vector $f(C)$ of a chemical graph $C$ and construct an ANN that maps $x=f(C)$ to a predicted value $\eta(x)$ of a chemical property $\pi$ to $C$. After this, we formulate an MILP that simulates the computation process of $f(C)$ from $C$ and that of $\eta(x)$ from $x$. Given a target value $y^*$ of the chemical property $\pi$, we infer a chemical graph $C^\dagger$ such that $\eta(f(C^\dagger))=y^*$ by solving the MILP. In this paper, we use linear regression to construct a prediction function $\eta$ instead of ANNs. For this, we derive an MILP formulation that simulates the computation process of a prediction function by linear regression. The results of computational experiments suggest our method can infer chemical graphs with around up to 50 non-hydrogen atoms.

On the Compressive Power of Boolean Threshold Autoencoders

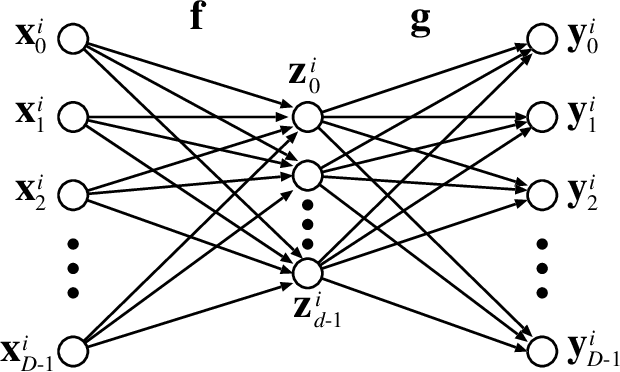
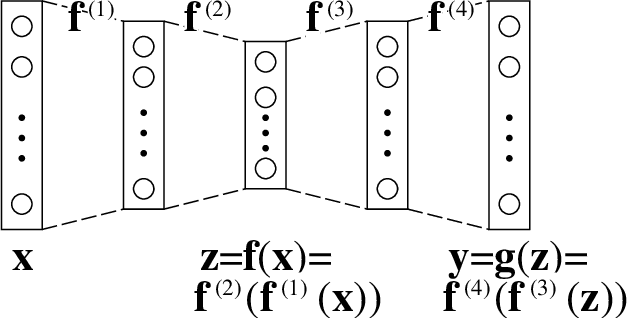
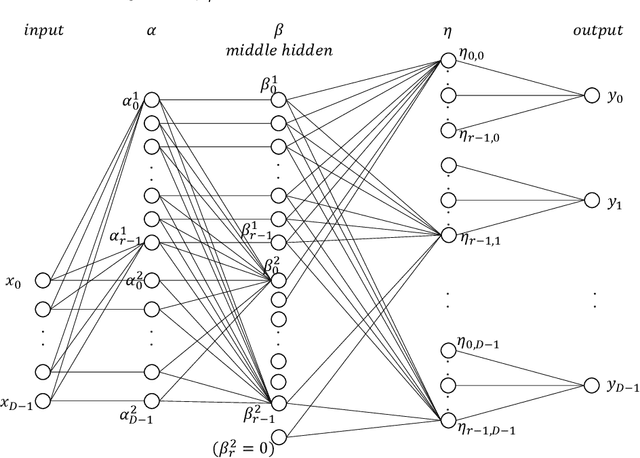
An autoencoder is a layered neural network whose structure can be viewed as consisting of an encoder, which compresses an input vector of dimension $D$ to a vector of low dimension $d$, and a decoder which transforms the low-dimensional vector back to the original input vector (or one that is very similar). In this paper we explore the compressive power of autoencoders that are Boolean threshold networks by studying the numbers of nodes and layers that are required to ensure that the numbers of nodes and layers that are required to ensure that each vector in a given set of distinct input binary vectors is transformed back to its original. We show that for any set of $n$ distinct vectors there exists a seven-layer autoencoder with the smallest possible middle layer, (i.e., its size is logarithmic in $n$), but that there is a set of $n$ vectors for which there is no three-layer autoencoder with a middle layer of the same size. In addition we present a kind of trade-off: if a considerably larger middle layer is permissible then a five-layer autoencoder does exist. We also study encoding by itself. The results we obtain suggest that it is the decoding that constitutes the bottleneck of autoencoding. For example, there always is a three-layer Boolean threshold encoder that compresses $n$ vectors into a dimension that is reduced to twice the logarithm of $n$.