A Discrete Perspective Towards the Construction of Sparse Probabilistic Boolean Networks

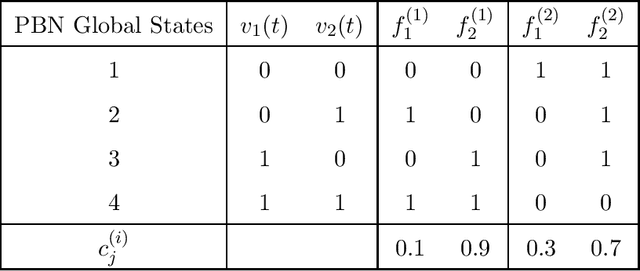
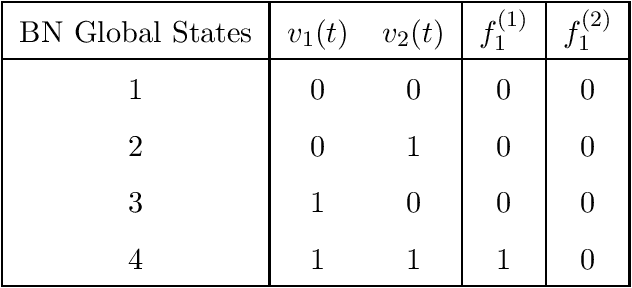
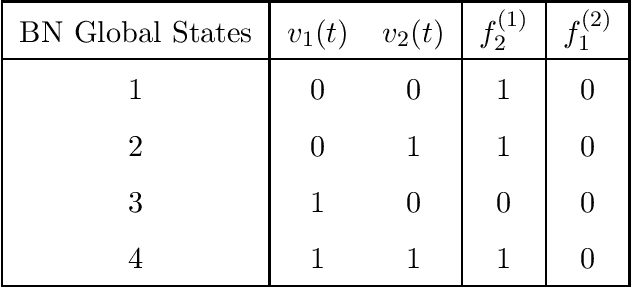
Boolean Network (BN) and its extension Probabilistic Boolean Network (PBN) are popular mathematical models for studying genetic regulatory networks. BNs and PBNs are also applied to model manufacturing systems, financial risk and healthcare service systems. In this paper, we propose a novel Greedy Entry Removal (GER) algorithm for constructing sparse PBNs. We derive theoretical upper bounds for both existing algorithms and the GER algorithm. Furthermore, we are the first to study the lower bound problem of the construction of sparse PBNs, and to derive a series of related theoretical results. In our numerical experiments based on both synthetic and practical data, GER gives the best performance among state-of-the-art sparse PBN construction algorithms and outputs sparsest possible decompositions on most of the transition probability matrices being tested.

On the Compressive Power of Boolean Threshold Autoencoders

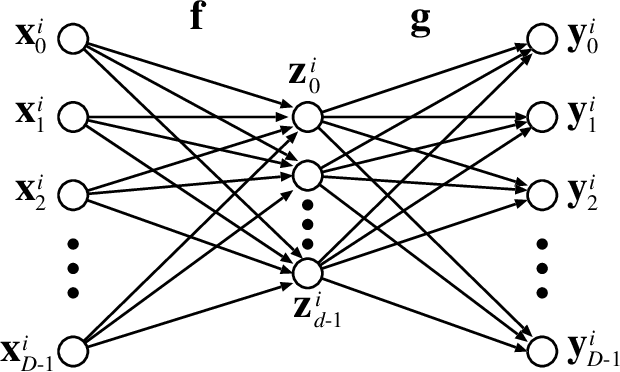
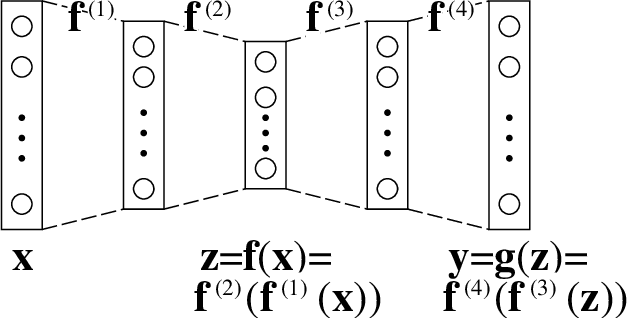
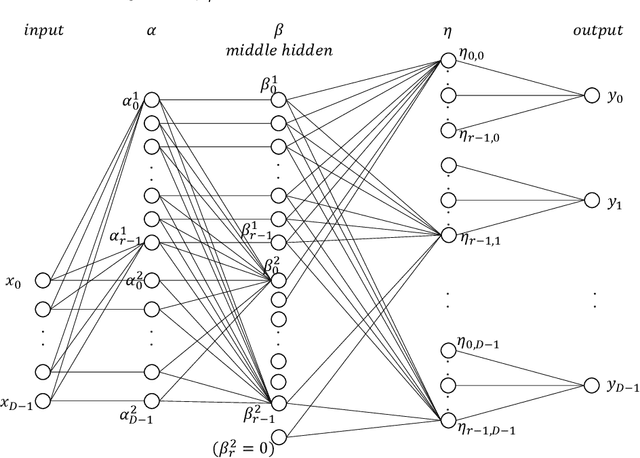
An autoencoder is a layered neural network whose structure can be viewed as consisting of an encoder, which compresses an input vector of dimension $D$ to a vector of low dimension $d$, and a decoder which transforms the low-dimensional vector back to the original input vector (or one that is very similar). In this paper we explore the compressive power of autoencoders that are Boolean threshold networks by studying the numbers of nodes and layers that are required to ensure that the numbers of nodes and layers that are required to ensure that each vector in a given set of distinct input binary vectors is transformed back to its original. We show that for any set of $n$ distinct vectors there exists a seven-layer autoencoder with the smallest possible middle layer, (i.e., its size is logarithmic in $n$), but that there is a set of $n$ vectors for which there is no three-layer autoencoder with a middle layer of the same size. In addition we present a kind of trade-off: if a considerably larger middle layer is permissible then a five-layer autoencoder does exist. We also study encoding by itself. The results we obtain suggest that it is the decoding that constitutes the bottleneck of autoencoding. For example, there always is a three-layer Boolean threshold encoder that compresses $n$ vectors into a dimension that is reduced to twice the logarithm of $n$.