Christopher H. Fok
A Discrete Perspective Towards the Construction of Sparse Probabilistic Boolean Networks
Jul 16, 2024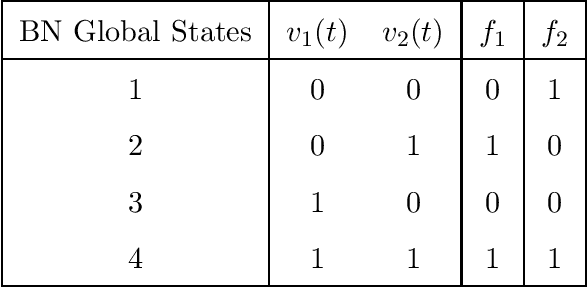
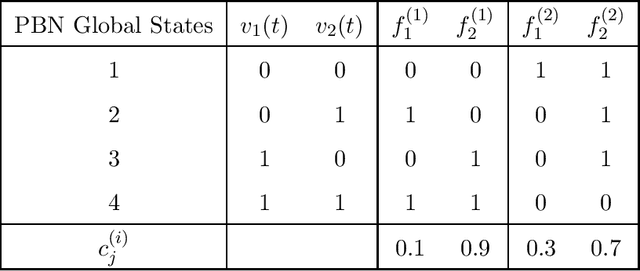
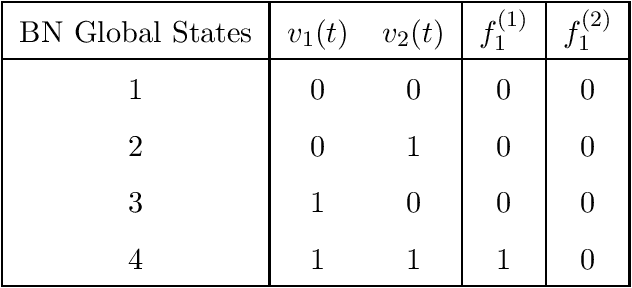
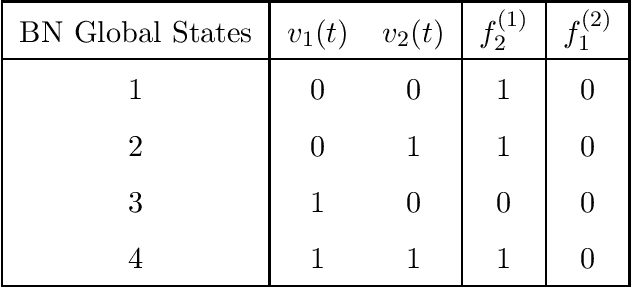
Abstract:Boolean Network (BN) and its extension Probabilistic Boolean Network (PBN) are popular mathematical models for studying genetic regulatory networks. BNs and PBNs are also applied to model manufacturing systems, financial risk and healthcare service systems. In this paper, we propose a novel Greedy Entry Removal (GER) algorithm for constructing sparse PBNs. We derive theoretical upper bounds for both existing algorithms and the GER algorithm. Furthermore, we are the first to study the lower bound problem of the construction of sparse PBNs, and to derive a series of related theoretical results. In our numerical experiments based on both synthetic and practical data, GER gives the best performance among state-of-the-art sparse PBN construction algorithms and outputs sparsest possible decompositions on most of the transition probability matrices being tested.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge