On the Size and Width of the Decoder of a Boolean Threshold Autoencoder
Paper and Code
Dec 21, 2021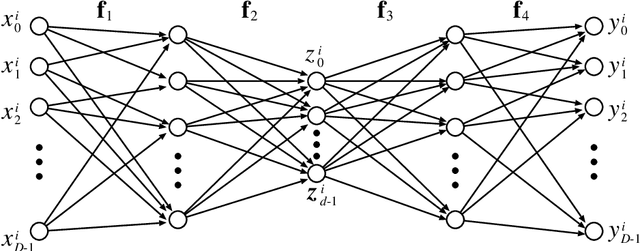



In this paper, we study the size and width of autoencoders consisting of Boolean threshold functions, where an autoencoder is a layered neural network whose structure can be viewed as consisting of an encoder, which compresses an input vector to a lower dimensional vector, and a decoder which transforms the low-dimensional vector back to the original input vector exactly (or approximately). We focus on the decoder part, and show that $\Omega(\sqrt{Dn/d})$ and $O(\sqrt{Dn})$ nodes are required to transform $n$ vectors in $d$-dimensional binary space to $D$-dimensional binary space. We also show that the width can be reduced if we allow small errors, where the error is defined as the average of the Hamming distance between each vector input to the encoder part and the resulting vector output by the decoder.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge