Hiroshi Nagamochi
Molecular Design Based on Integer Programming and Splitting Data Sets by Hyperplanes
Apr 27, 2023
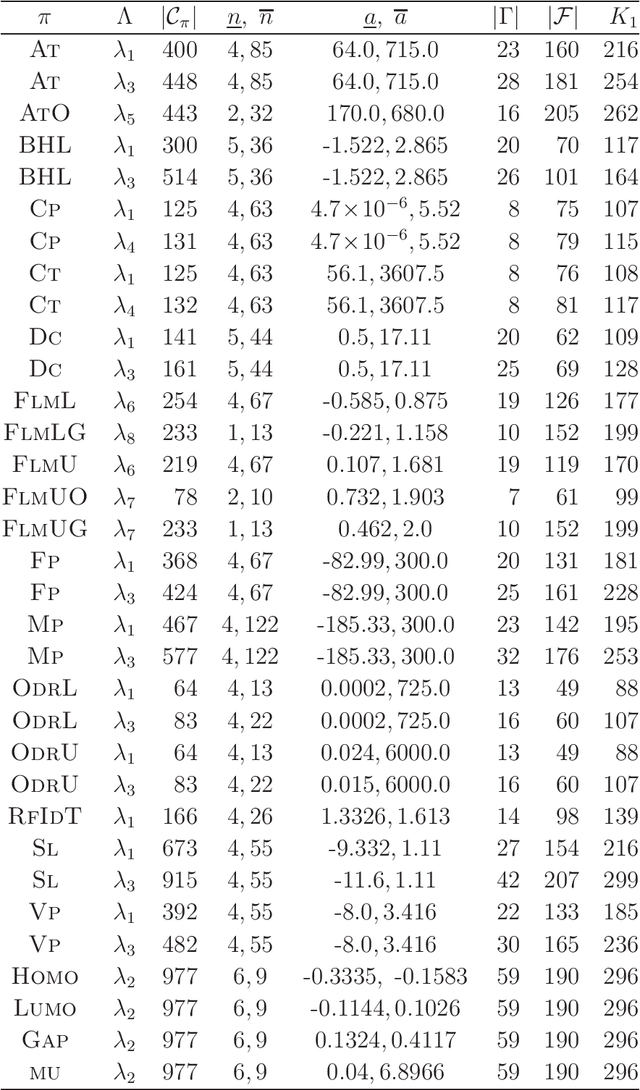

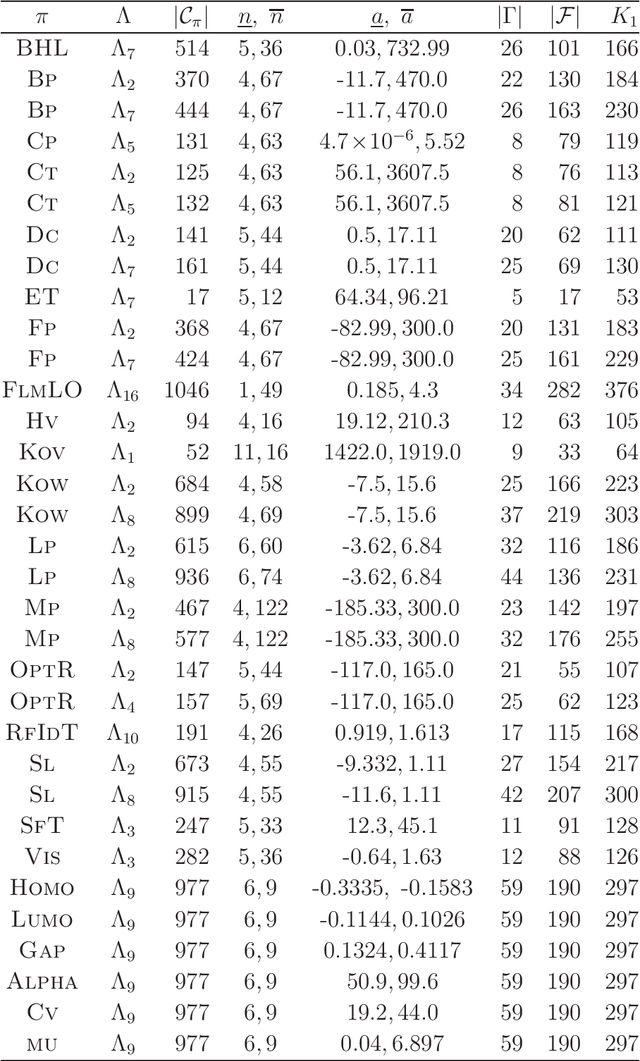
Abstract:A novel framework for designing the molecular structure of chemical compounds with a desired chemical property has recently been proposed. The framework infers a desired chemical graph by solving a mixed integer linear program (MILP) that simulates the computation process of a feature function defined by a two-layered model on chemical graphs and a prediction function constructed by a machine learning method. To improve the learning performance of prediction functions in the framework, we design a method that splits a given data set $\mathcal{C}$ into two subsets $\mathcal{C}^{(i)},i=1,2$ by a hyperplane in a chemical space so that most compounds in the first (resp., second) subset have observed values lower (resp., higher) than a threshold $\theta$. We construct a prediction function $\psi$ to the data set $\mathcal{C}$ by combining prediction functions $\psi_i,i=1,2$ each of which is constructed on $\mathcal{C}^{(i)}$ independently. The results of our computational experiments suggest that the proposed method improved the learning performance for several chemical properties to which a good prediction function has been difficult to construct.
Molecular Design Based on Integer Programming and Quadratic Descriptors in a Two-layered Model
Sep 13, 2022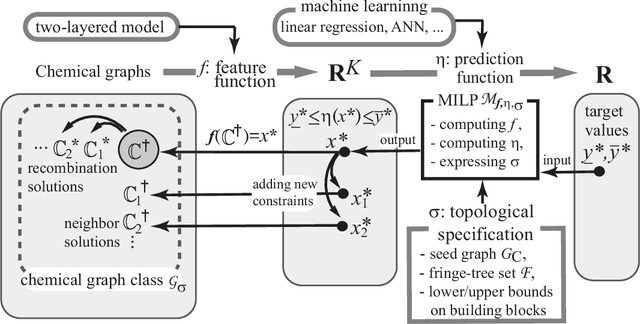
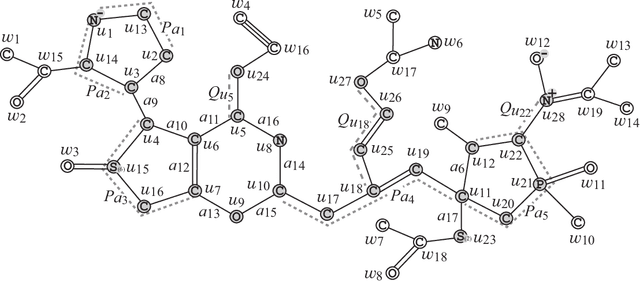
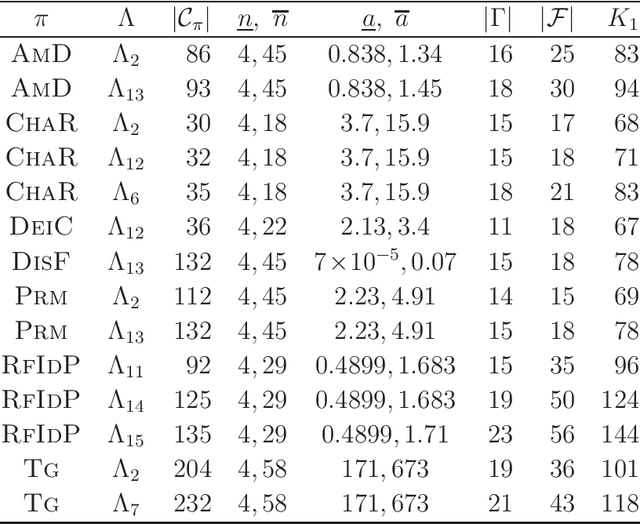
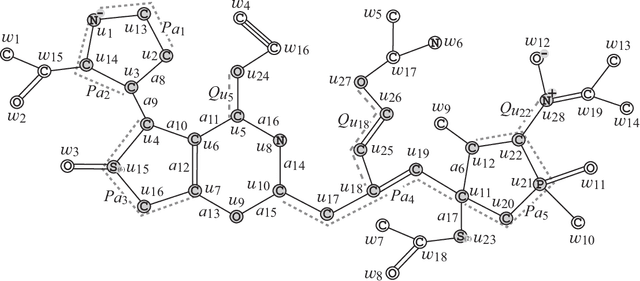
Abstract:A novel framework has recently been proposed for designing the molecular structure of chemical compounds with a desired chemical property, where design of novel drugs is an important topic in bioinformatics and chemo-informatics. The framework infers a desired chemical graph by solving a mixed integer linear program (MILP) that simulates the computation process of a feature function defined by a two-layered model on chemical graphs and a prediction function constructed by a machine learning method. A set of graph theoretical descriptors in the feature function plays a key role to derive a compact formulation of such an MILP. To improve the learning performance of prediction functions in the framework maintaining the compactness of the MILP, this paper utilizes the product of two of those descriptors as a new descriptor and then designs a method of reducing the number of descriptors. The results of our computational experiments suggest that the proposed method improved the learning performance for many chemical properties and can infer a chemical structure with up to 50 non-hydrogen atoms.
A Method for Inferring Polymers Based on Linear Regression and Integer Programming
Aug 24, 2021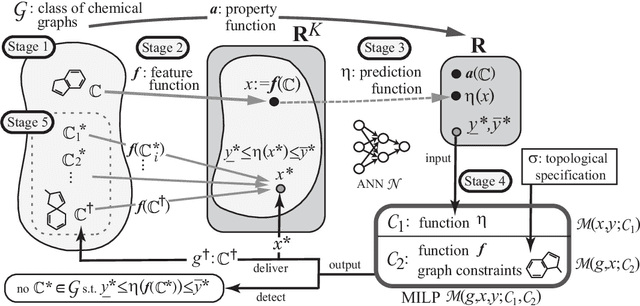
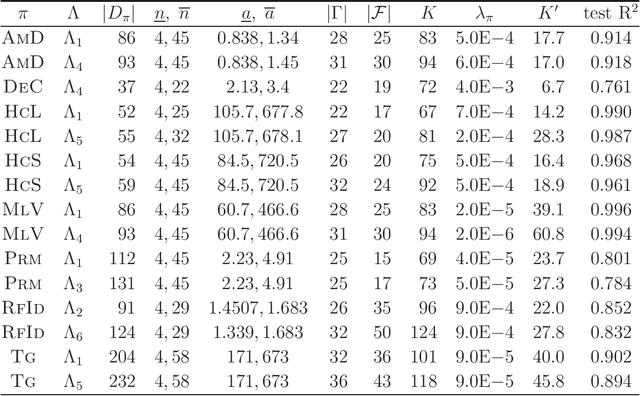

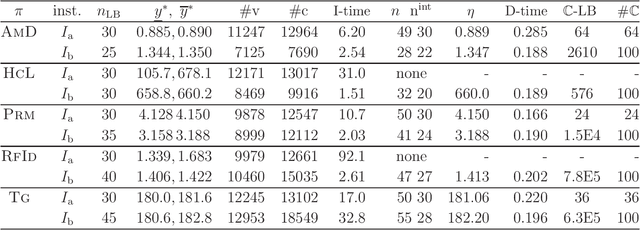
Abstract:A novel framework has recently been proposed for designing the molecular structure of chemical compounds with a desired chemical property using both artificial neural networks and mixed integer linear programming. In this paper, we design a new method for inferring a polymer based on the framework. For this, we introduce a new way of representing a polymer as a form of monomer and define new descriptors that feature the structure of polymers. We also use linear regression as a building block of constructing a prediction function in the framework. The results of our computational experiments reveal a set of chemical properties on polymers to which a prediction function constructed with linear regression performs well. We also observe that the proposed method can infer polymers with up to 50 non-hydrogen atoms in a monomer form.
Molecular Design Based on Artificial Neural Networks, Integer Programming and Grid Neighbor Search
Aug 23, 2021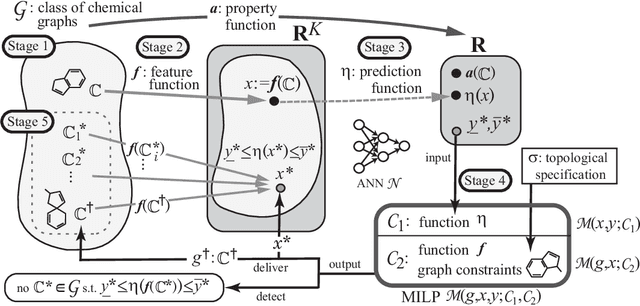
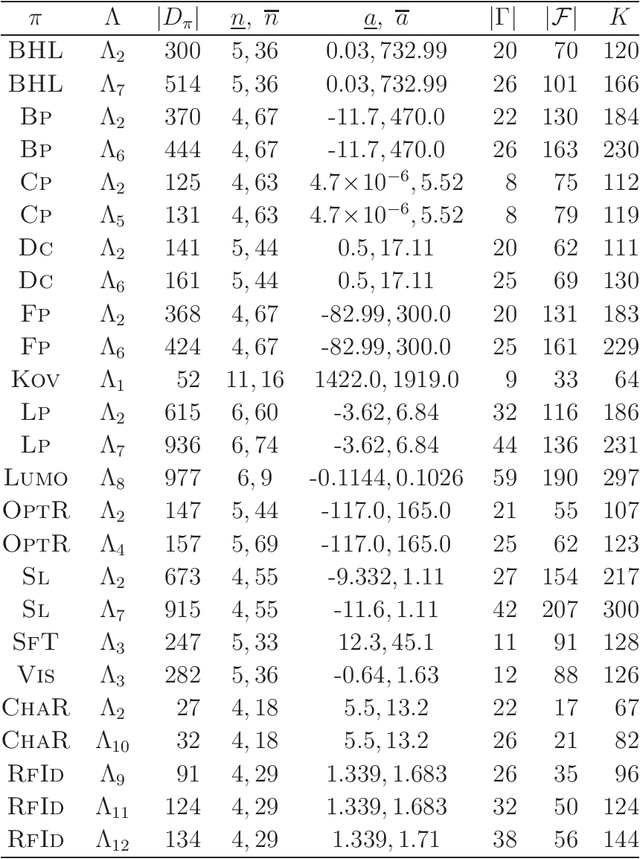
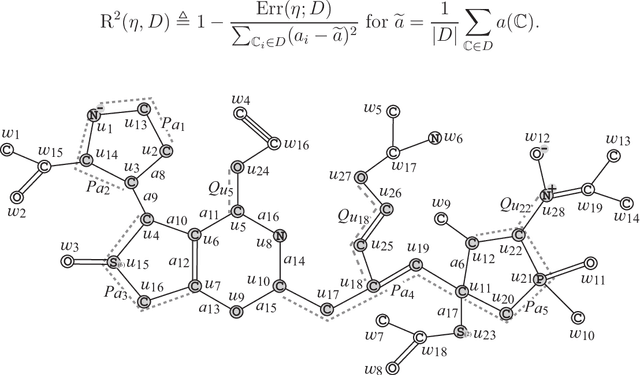
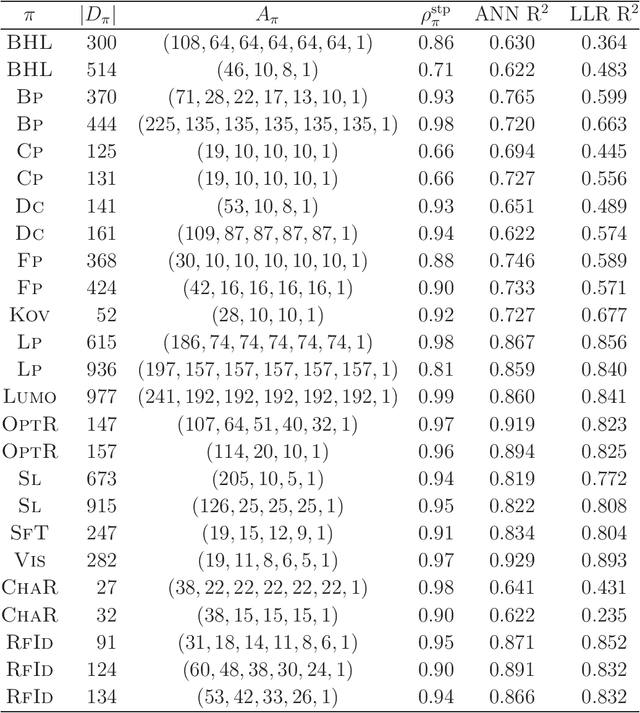
Abstract:A novel framework has recently been proposed for designing the molecular structure of chemical compounds with a desired chemical property using both artificial neural networks and mixed integer linear programming. In the framework, a chemical graph with a target chemical value is inferred as a feasible solution of a mixed integer linear program that represents a prediction function and other requirements on the structure of graphs. In this paper, we propose a procedure for generating other feasible solutions of the mixed integer linear program by searching the neighbor of output chemical graph in a search space. The procedure is combined in the framework as a new building block. The results of our computational experiments suggest that the proposed method can generate an additional number of new chemical graphs with up to 50 non-hydrogen atoms.
An Inverse QSAR Method Based on Linear Regression and Integer Programming
Jul 13, 2021
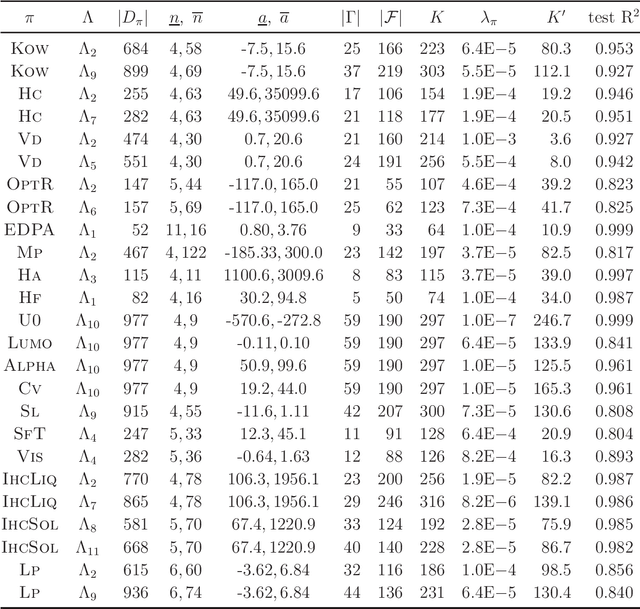
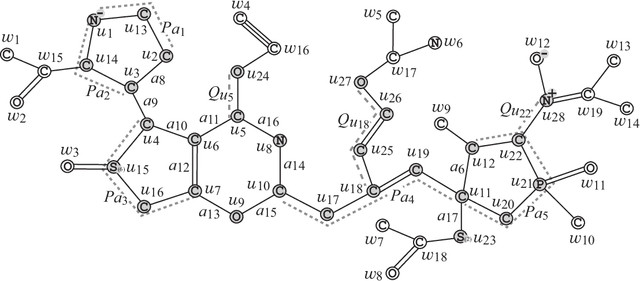
Abstract:Recently a novel framework has been proposed for designing the molecular structure of chemical compounds using both artificial neural networks (ANNs) and mixed integer linear programming (MILP). In the framework, we first define a feature vector $f(C)$ of a chemical graph $C$ and construct an ANN that maps $x=f(C)$ to a predicted value $\eta(x)$ of a chemical property $\pi$ to $C$. After this, we formulate an MILP that simulates the computation process of $f(C)$ from $C$ and that of $\eta(x)$ from $x$. Given a target value $y^*$ of the chemical property $\pi$, we infer a chemical graph $C^\dagger$ such that $\eta(f(C^\dagger))=y^*$ by solving the MILP. In this paper, we use linear regression to construct a prediction function $\eta$ instead of ANNs. For this, we derive an MILP formulation that simulates the computation process of a prediction function by linear regression. The results of computational experiments suggest our method can infer chemical graphs with around up to 50 non-hydrogen atoms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge