An Inverse QSAR Method Based on Linear Regression and Integer Programming
Paper and Code
Jul 13, 2021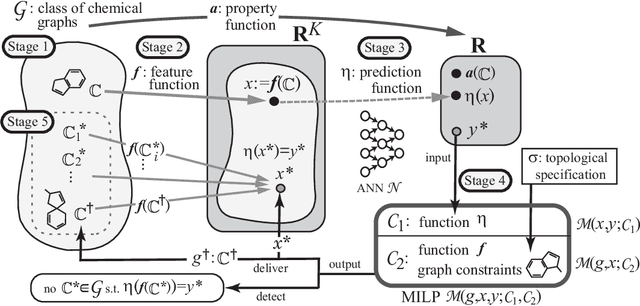
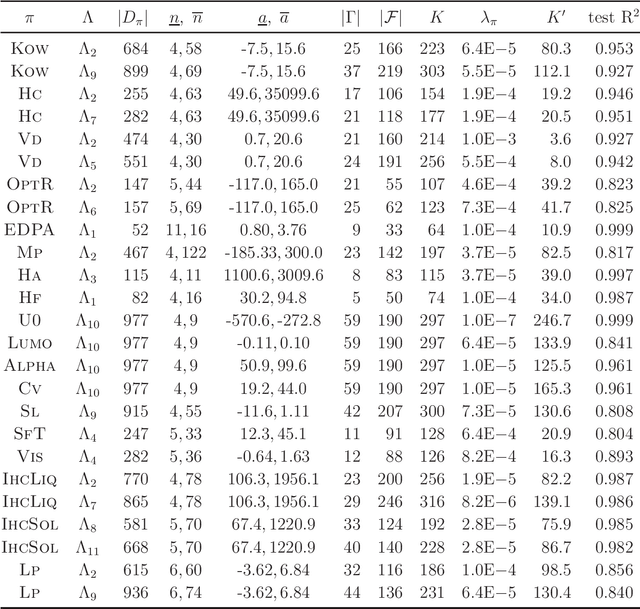
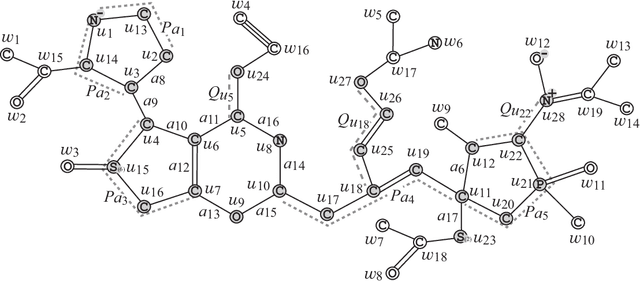
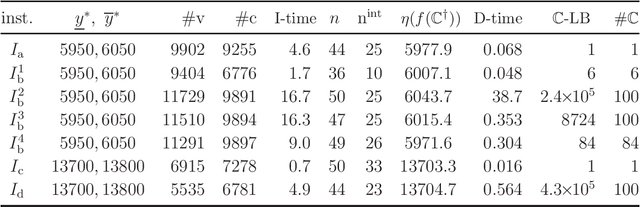
Recently a novel framework has been proposed for designing the molecular structure of chemical compounds using both artificial neural networks (ANNs) and mixed integer linear programming (MILP). In the framework, we first define a feature vector $f(C)$ of a chemical graph $C$ and construct an ANN that maps $x=f(C)$ to a predicted value $\eta(x)$ of a chemical property $\pi$ to $C$. After this, we formulate an MILP that simulates the computation process of $f(C)$ from $C$ and that of $\eta(x)$ from $x$. Given a target value $y^*$ of the chemical property $\pi$, we infer a chemical graph $C^\dagger$ such that $\eta(f(C^\dagger))=y^*$ by solving the MILP. In this paper, we use linear regression to construct a prediction function $\eta$ instead of ANNs. For this, we derive an MILP formulation that simulates the computation process of a prediction function by linear regression. The results of computational experiments suggest our method can infer chemical graphs with around up to 50 non-hydrogen atoms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge