A comprehensive study of spike and slab shrinkage priors for structurally sparse Bayesian neural networks

Network complexity and computational efficiency have become increasingly significant aspects of deep learning. Sparse deep learning addresses these challenges by recovering a sparse representation of the underlying target function by reducing heavily over-parameterized deep neural networks. Specifically, deep neural architectures compressed via structured sparsity (e.g. node sparsity) provide low latency inference, higher data throughput, and reduced energy consumption. In this paper, we explore two well-established shrinkage techniques, Lasso and Horseshoe, for model compression in Bayesian neural networks. To this end, we propose structurally sparse Bayesian neural networks which systematically prune excessive nodes with (i) Spike-and-Slab Group Lasso (SS-GL), and (ii) Spike-and-Slab Group Horseshoe (SS-GHS) priors, and develop computationally tractable variational inference including continuous relaxation of Bernoulli variables. We establish the contraction rates of the variational posterior of our proposed models as a function of the network topology, layer-wise node cardinalities, and bounds on the network weights. We empirically demonstrate the competitive performance of our models compared to the baseline models in prediction accuracy, model compression, and inference latency.

Feature Selection integrated Deep Learning for Ultrahigh Dimensional and Highly Correlated Feature Space

In recent years, deep learning has been a topic of interest in almost all disciplines due to its impressive empirical success in analyzing complex data sets, such as imaging, genetics, climate, and medical data. While most of the developments are treated as black-box machines, there is an increasing interest in interpretable, reliable, and robust deep learning models applicable to a broad class of applications. Feature-selected deep learning is proven to be promising in this regard. However, the recent developments do not address the situations of ultra-high dimensional and highly correlated feature selection in addition to the high noise level. In this article, we propose a novel screening and cleaning strategy with the aid of deep learning for the cluster-level discovery of highly correlated predictors with a controlled error rate. A thorough empirical evaluation over a wide range of simulated scenarios demonstrates the effectiveness of the proposed method by achieving high power while having a minimal number of false discoveries. Furthermore, we implemented the algorithm in the riboflavin (vitamin $B_2$) production dataset in the context of understanding the possible genetic association with riboflavin production. The gain of the proposed methodology is illustrated by achieving lower prediction error compared to other state-of-the-art methods.

Sequential Bayesian Neural Subnetwork Ensembles

Deep neural network ensembles that appeal to model diversity have been used successfully to improve predictive performance and model robustness in several applications. Whereas, it has recently been shown that sparse subnetworks of dense models can match the performance of their dense counterparts and increase their robustness while effectively decreasing the model complexity. However, most ensembling techniques require multiple parallel and costly evaluations and have been proposed primarily with deterministic models, whereas sparsity induction has been mostly done through ad-hoc pruning. We propose sequential ensembling of dynamic Bayesian neural subnetworks that systematically reduce model complexity through sparsity-inducing priors and generate diverse ensembles in a single forward pass of the model. The ensembling strategy consists of an exploration phase that finds high-performing regions of the parameter space and multiple exploitation phases that effectively exploit the compactness of the sparse model to quickly converge to different minima in the energy landscape corresponding to high-performing subnetworks yielding diverse ensembles. We empirically demonstrate that our proposed approach surpasses the baselines of the dense frequentist and Bayesian ensemble models in prediction accuracy, uncertainty estimation, and out-of-distribution (OoD) robustness on CIFAR10, CIFAR100 datasets, and their out-of-distribution variants: CIFAR10-C, CIFAR100-C induced by corruptions. Furthermore, we found that our approach produced the most diverse ensembles compared to the approaches with a single forward pass and even compared to the approaches with multiple forward passes in some cases.

Coupled Support Tensor Machine Classification for Multimodal Neuroimaging Data

Multimodal data arise in various applications where information about the same phenomenon is acquired from multiple sensors and across different imaging modalities. Learning from multimodal data is of great interest in machine learning and statistics research as this offers the possibility of capturing complementary information among modalities. Multimodal modeling helps to explain the interdependence between heterogeneous data sources, discovers new insights that may not be available from a single modality, and improves decision-making. Recently, coupled matrix-tensor factorization has been introduced for multimodal data fusion to jointly estimate latent factors and identify complex interdependence among the latent factors. However, most of the prior work on coupled matrix-tensor factors focuses on unsupervised learning and there is little work on supervised learning using the jointly estimated latent factors. This paper considers the multimodal tensor data classification problem. A Coupled Support Tensor Machine (C-STM) built upon the latent factors jointly estimated from the Advanced Coupled Matrix Tensor Factorization (ACMTF) is proposed. C-STM combines individual and shared latent factors with multiple kernels and estimates a maximal-margin classifier for coupled matrix tensor data. The classification risk of C-STM is shown to converge to the optimal Bayes risk, making it a statistically consistent rule. C-STM is validated through simulation studies as well as a simultaneous EEG-fMRI analysis. The empirical evidence shows that C-STM can utilize information from multiple sources and provide a better classification performance than traditional single-mode classifiers.

Layer Adaptive Node Selection in Bayesian Neural Networks: Statistical Guarantees and Implementation Details

Sparse deep neural networks have proven to be efficient for predictive model building in large-scale studies. Although several works have studied theoretical and numerical properties of sparse neural architectures, they have primarily focused on the edge selection. Sparsity through edge selection might be intuitively appealing; however, it does not necessarily reduce the structural complexity of a network. Instead pruning excessive nodes in each layer leads to a structurally sparse network which would have lower computational complexity and memory footprint. We propose a Bayesian sparse solution using spike-and-slab Gaussian priors to allow for node selection during training. The use of spike-and-slab prior alleviates the need of an ad-hoc thresholding rule for pruning redundant nodes from a network. In addition, we adopt a variational Bayes approach to circumvent the computational challenges of traditional Markov Chain Monte Carlo (MCMC) implementation. In the context of node selection, we establish the fundamental result of variational posterior consistency together with the characterization of prior parameters. In contrast to the previous works, our theoretical development relaxes the assumptions of the equal number of nodes and uniform bounds on all network weights, thereby accommodating sparse networks with layer-dependent node structures or coefficient bounds. With a layer-wise characterization of prior inclusion probabilities, we also discuss optimal contraction rates of the variational posterior. Finally, we provide empirical evidence to substantiate that our theoretical work facilitates layer-wise optimal node recovery together with competitive predictive performance.

TEC: Tensor Ensemble Classifier for Big Data

Tensor (multidimensional array) classification problem has become very popular in modern applications such as image recognition and high dimensional spatio-temporal data analysis. Support Tensor Machine (STM) classifier, which is extended from the support vector machine, takes CANDECOMP / Parafac (CP) form of tensor data as input and predicts the data labels. The distribution-free and statistically consistent properties of STM highlight its potential in successfully handling wide varieties of data applications. Training a STM can be computationally expensive with high-dimensional tensors. However, reducing the size of tensor with a random projection technique can reduce the computational time and cost, making it feasible to handle large size tensors on regular machines. We name an STM estimated with randomly projected tensor as Random Projection-based Support Tensor Machine (RPSTM). In this work, we propose a Tensor Ensemble Classifier (TEC), which aggregates multiple RPSTMs for big tensor classification. TEC utilizes the ensemble idea to minimize the excessive classification risk brought by random projection, providing statistically consistent predictions while taking the computational advantage of RPSTM. Since each RPSTM can be estimated independently, TEC can further take advantage of parallel computing techniques and be more computationally efficient. The theoretical and numerical results demonstrate the decent performance of TEC model in high-dimensional tensor classification problems. The model prediction is statistically consistent as its risk is shown to converge to the optimal Bayes risk. Besides, we highlight the trade-off between the computational cost and the prediction risk for TEC model. The method is validated by extensive simulation and a real data example. We prepare a python package for applying TEC, which is available at our GitHub.

Variational Bayes Neural Network: Posterior Consistency, Classification Accuracy and Computational Challenges

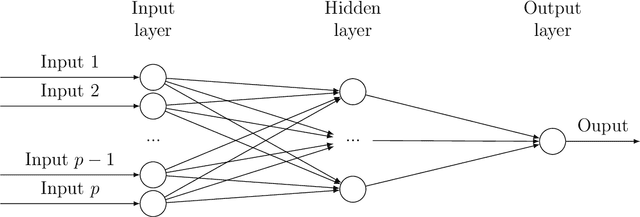
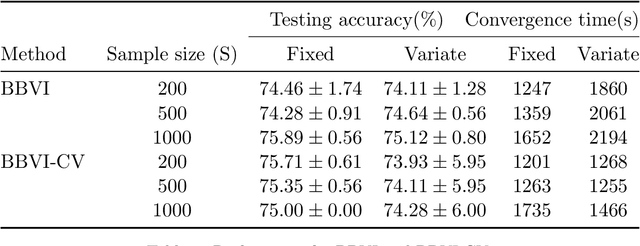
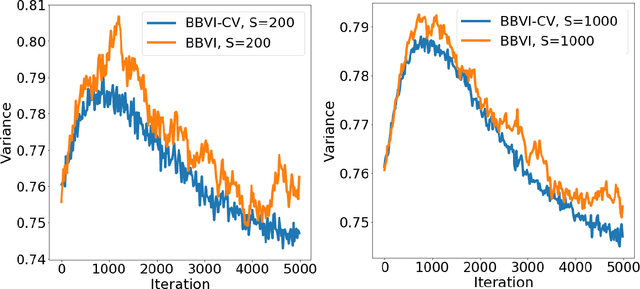
Bayesian neural network models (BNN) have re-surged in recent years due to the advancement of scalable computations and its utility in solving complex prediction problems in a wide variety of applications. Despite the popularity and usefulness of BNN, the conventional Markov Chain Monte Carlo based implementation suffers from high computational cost, limiting the use of this powerful technique in large scale studies. The variational Bayes inference has become a viable alternative to circumvent some of the computational issues. Although the approach is popular in machine learning, its application in statistics is somewhat limited. This paper develops a variational Bayesian neural network estimation methodology and related statistical theory. The numerical algorithms and their implementational are discussed in detail. The theory for posterior consistency, a desirable property in nonparametric Bayesian statistics, is also developed. This theory provides an assessment of prediction accuracy and guidelines for characterizing the prior distributions and variational family. The loss of using a variational posterior over the true posterior has also been quantified. The development is motivated by an important biomedical engineering application, namely building predictive tools for the transition from mild cognitive impairment to Alzheimer's disease. The predictors are multi-modal and may involve complex interactive relations.

Statistical Foundation of Variational Bayes Neural Networks

Despite the popularism of Bayesian neural networks in recent years, its use is somewhat limited in complex and big data situations due to the computational cost associated with full posterior evaluations. Variational Bayes (VB) provides a useful alternative to circumvent the computational cost and time complexity associated with the generation of samples from the true posterior using Markov Chain Monte Carlo (MCMC) techniques. The efficacy of the VB methods is well established in machine learning literature. However, its potential broader impact is hindered due to a lack of theoretical validity from a statistical perspective. However there are few results which revolve around the theoretical properties of VB, especially in non-parametric problems. In this paper, we establish the fundamental result of posterior consistency for the mean-field variational posterior (VP) for a feed-forward artificial neural network model. The paper underlines the conditions needed to guarantee that the VP concentrates around Hellinger neighborhoods of the true density function. Additionally, the role of the scale parameter and its influence on the convergence rates has also been discussed. The paper mainly relies on two results (1) the rate at which the true posterior grows (2) the rate at which the KL-distance between the posterior and variational posterior grows. The theory provides a guideline of building prior distributions for Bayesian NN models along with an assessment of accuracy of the corresponding VB implementation.

Variational Inference with Vine Copulas: An efficient Approach for Bayesian Computer Model Calibration

With the advancements of computer architectures, the use of computational models proliferates to solve complex problems in many scientific applications such as nuclear physics and climate research. However, the potential of such models is often hindered because they tend to be computationally expensive and consequently ill-fitting for uncertainty quantification. Furthermore, they are usually not calibrated with real-time observations. We develop a computationally efficient algorithm based on variational Bayes inference (VBI) for calibration of computer models with Gaussian processes. Unfortunately, the speed and scalability of VBI diminishes when applied to the calibration framework with dependent data. To preserve the efficiency of VBI, we adopt a pairwise decomposition of the data likelihood using vine copulas that separate the information on dependence structure in data from their marginal distributions. We provide both theoretical and empirical evidence for the computational scalability of our methodology and describe all the necessary details for an efficient implementation of the proposed algorithm. We also demonstrated the opportunities given by our method for practitioners on a real data example through calibration of the Liquid Drop Model of nuclear binding energies.