A comprehensive study of spike and slab shrinkage priors for structurally sparse Bayesian neural networks

Network complexity and computational efficiency have become increasingly significant aspects of deep learning. Sparse deep learning addresses these challenges by recovering a sparse representation of the underlying target function by reducing heavily over-parameterized deep neural networks. Specifically, deep neural architectures compressed via structured sparsity (e.g. node sparsity) provide low latency inference, higher data throughput, and reduced energy consumption. In this paper, we explore two well-established shrinkage techniques, Lasso and Horseshoe, for model compression in Bayesian neural networks. To this end, we propose structurally sparse Bayesian neural networks which systematically prune excessive nodes with (i) Spike-and-Slab Group Lasso (SS-GL), and (ii) Spike-and-Slab Group Horseshoe (SS-GHS) priors, and develop computationally tractable variational inference including continuous relaxation of Bernoulli variables. We establish the contraction rates of the variational posterior of our proposed models as a function of the network topology, layer-wise node cardinalities, and bounds on the network weights. We empirically demonstrate the competitive performance of our models compared to the baseline models in prediction accuracy, model compression, and inference latency.

Sequential Bayesian Neural Subnetwork Ensembles

Deep neural network ensembles that appeal to model diversity have been used successfully to improve predictive performance and model robustness in several applications. Whereas, it has recently been shown that sparse subnetworks of dense models can match the performance of their dense counterparts and increase their robustness while effectively decreasing the model complexity. However, most ensembling techniques require multiple parallel and costly evaluations and have been proposed primarily with deterministic models, whereas sparsity induction has been mostly done through ad-hoc pruning. We propose sequential ensembling of dynamic Bayesian neural subnetworks that systematically reduce model complexity through sparsity-inducing priors and generate diverse ensembles in a single forward pass of the model. The ensembling strategy consists of an exploration phase that finds high-performing regions of the parameter space and multiple exploitation phases that effectively exploit the compactness of the sparse model to quickly converge to different minima in the energy landscape corresponding to high-performing subnetworks yielding diverse ensembles. We empirically demonstrate that our proposed approach surpasses the baselines of the dense frequentist and Bayesian ensemble models in prediction accuracy, uncertainty estimation, and out-of-distribution (OoD) robustness on CIFAR10, CIFAR100 datasets, and their out-of-distribution variants: CIFAR10-C, CIFAR100-C induced by corruptions. Furthermore, we found that our approach produced the most diverse ensembles compared to the approaches with a single forward pass and even compared to the approaches with multiple forward passes in some cases.

Layer Adaptive Node Selection in Bayesian Neural Networks: Statistical Guarantees and Implementation Details

Sparse deep neural networks have proven to be efficient for predictive model building in large-scale studies. Although several works have studied theoretical and numerical properties of sparse neural architectures, they have primarily focused on the edge selection. Sparsity through edge selection might be intuitively appealing; however, it does not necessarily reduce the structural complexity of a network. Instead pruning excessive nodes in each layer leads to a structurally sparse network which would have lower computational complexity and memory footprint. We propose a Bayesian sparse solution using spike-and-slab Gaussian priors to allow for node selection during training. The use of spike-and-slab prior alleviates the need of an ad-hoc thresholding rule for pruning redundant nodes from a network. In addition, we adopt a variational Bayes approach to circumvent the computational challenges of traditional Markov Chain Monte Carlo (MCMC) implementation. In the context of node selection, we establish the fundamental result of variational posterior consistency together with the characterization of prior parameters. In contrast to the previous works, our theoretical development relaxes the assumptions of the equal number of nodes and uniform bounds on all network weights, thereby accommodating sparse networks with layer-dependent node structures or coefficient bounds. With a layer-wise characterization of prior inclusion probabilities, we also discuss optimal contraction rates of the variational posterior. Finally, we provide empirical evidence to substantiate that our theoretical work facilitates layer-wise optimal node recovery together with competitive predictive performance.

Variational Bayes Neural Network: Posterior Consistency, Classification Accuracy and Computational Challenges

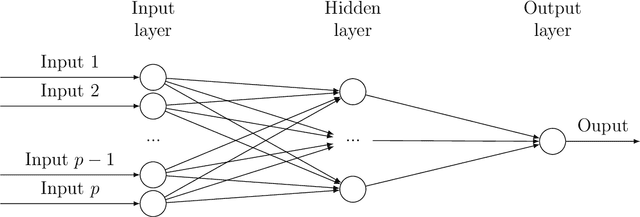
Bayesian neural network models (BNN) have re-surged in recent years due to the advancement of scalable computations and its utility in solving complex prediction problems in a wide variety of applications. Despite the popularity and usefulness of BNN, the conventional Markov Chain Monte Carlo based implementation suffers from high computational cost, limiting the use of this powerful technique in large scale studies. The variational Bayes inference has become a viable alternative to circumvent some of the computational issues. Although the approach is popular in machine learning, its application in statistics is somewhat limited. This paper develops a variational Bayesian neural network estimation methodology and related statistical theory. The numerical algorithms and their implementational are discussed in detail. The theory for posterior consistency, a desirable property in nonparametric Bayesian statistics, is also developed. This theory provides an assessment of prediction accuracy and guidelines for characterizing the prior distributions and variational family. The loss of using a variational posterior over the true posterior has also been quantified. The development is motivated by an important biomedical engineering application, namely building predictive tools for the transition from mild cognitive impairment to Alzheimer's disease. The predictors are multi-modal and may involve complex interactive relations.

Statistical Foundation of Variational Bayes Neural Networks

Despite the popularism of Bayesian neural networks in recent years, its use is somewhat limited in complex and big data situations due to the computational cost associated with full posterior evaluations. Variational Bayes (VB) provides a useful alternative to circumvent the computational cost and time complexity associated with the generation of samples from the true posterior using Markov Chain Monte Carlo (MCMC) techniques. The efficacy of the VB methods is well established in machine learning literature. However, its potential broader impact is hindered due to a lack of theoretical validity from a statistical perspective. However there are few results which revolve around the theoretical properties of VB, especially in non-parametric problems. In this paper, we establish the fundamental result of posterior consistency for the mean-field variational posterior (VP) for a feed-forward artificial neural network model. The paper underlines the conditions needed to guarantee that the VP concentrates around Hellinger neighborhoods of the true density function. Additionally, the role of the scale parameter and its influence on the convergence rates has also been discussed. The paper mainly relies on two results (1) the rate at which the true posterior grows (2) the rate at which the KL-distance between the posterior and variational posterior grows. The theory provides a guideline of building prior distributions for Bayesian NN models along with an assessment of accuracy of the corresponding VB implementation.