Variational Bayes Neural Network: Posterior Consistency, Classification Accuracy and Computational Challenges
Paper and Code
Nov 19, 2020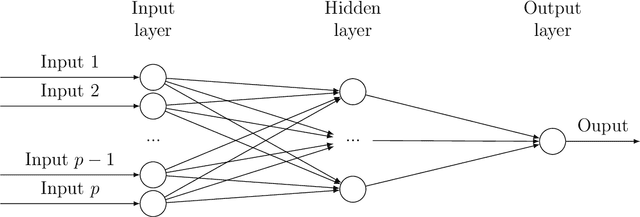

Bayesian neural network models (BNN) have re-surged in recent years due to the advancement of scalable computations and its utility in solving complex prediction problems in a wide variety of applications. Despite the popularity and usefulness of BNN, the conventional Markov Chain Monte Carlo based implementation suffers from high computational cost, limiting the use of this powerful technique in large scale studies. The variational Bayes inference has become a viable alternative to circumvent some of the computational issues. Although the approach is popular in machine learning, its application in statistics is somewhat limited. This paper develops a variational Bayesian neural network estimation methodology and related statistical theory. The numerical algorithms and their implementational are discussed in detail. The theory for posterior consistency, a desirable property in nonparametric Bayesian statistics, is also developed. This theory provides an assessment of prediction accuracy and guidelines for characterizing the prior distributions and variational family. The loss of using a variational posterior over the true posterior has also been quantified. The development is motivated by an important biomedical engineering application, namely building predictive tools for the transition from mild cognitive impairment to Alzheimer's disease. The predictors are multi-modal and may involve complex interactive relations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge