Circuit Partitioning Using Large Language Models for Quantum Compilation and Simulations

We are in the midst of the noisy intermediate-scale quantum (NISQ) era, where quantum computers are limited by noisy gates, some of which are more error-prone than others and can render the final computation incomprehensible. Quantum circuit compilation algorithms attempt to minimize these noisy gates when mapping quantum algorithms onto quantum hardware but face computational challenges that restrict their application to circuits with no more than 5-6 qubits, necessitating the need to partition large circuits before the application of noisy quantum gate minimization algorithms. The existing generation of these algorithms is heuristic in nature and does not account for downstream gate minimization tasks. Large language models (LLMs) have the potential to change this and help improve quantum circuit partitions. This paper investigates the use of LLMs, such as Llama and Mistral, for partitioning quantum circuits by capitalizing on their abilities to understand and generate code, including QASM. Specifically, we teach LLMs to partition circuits using the quick partition approach of the Berkeley Quantum Synthesis Toolkit. Through experimental evaluations, we show that careful fine-tuning of open source LLMs enables us to obtain an accuracy of 53.4% for the partition task while over-the-shelf LLMs are unable to correctly partition circuits, using standard 1-shot and few-shot training approaches.

An Extension of Fano's Inequality for Characterizing Model Susceptibility to Membership Inference Attacks

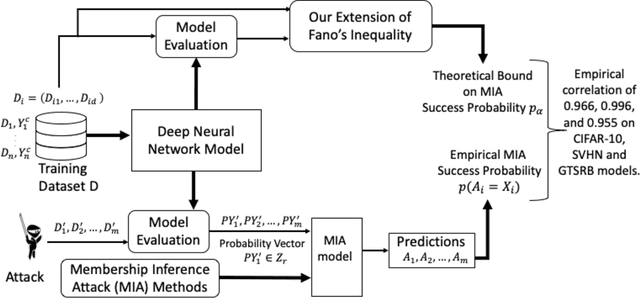
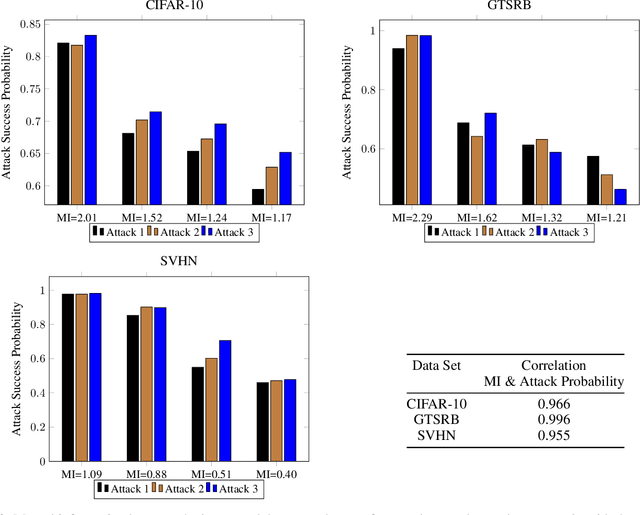
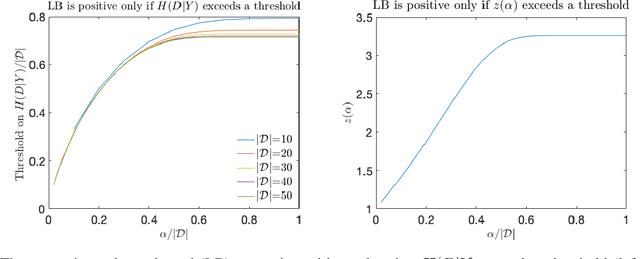
Deep neural networks have been shown to be vulnerable to membership inference attacks wherein the attacker aims to detect whether specific input data were used to train the model. These attacks can potentially leak private or proprietary data. We present a new extension of Fano's inequality and employ it to theoretically establish that the probability of success for a membership inference attack on a deep neural network can be bounded using the mutual information between its inputs and its activations. This enables the use of mutual information to measure the susceptibility of a DNN model to membership inference attacks. In our empirical evaluation, we show that the correlation between the mutual information and the susceptibility of the DNN model to membership inference attacks is 0.966, 0.996, and 0.955 for CIFAR-10, SVHN and GTSRB models, respectively.

Attribution-driven Causal Analysis for Detection of Adversarial Examples

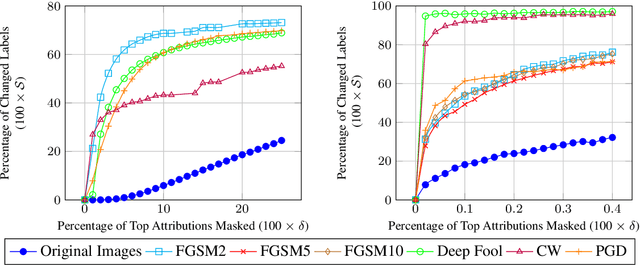
Attribution methods have been developed to explain the decision of a machine learning model on a given input. We use the Integrated Gradient method for finding attributions to define the causal neighborhood of an input by incrementally masking high attribution features. We study the robustness of machine learning models on benign and adversarial inputs in this neighborhood. Our study indicates that benign inputs are robust to the masking of high attribution features but adversarial inputs generated by the state-of-the-art adversarial attack methods such as DeepFool, FGSM, CW and PGD, are not robust to such masking. Further, our study demonstrates that this concentration of high-attribution features responsible for the incorrect decision is more pronounced in physically realizable adversarial examples. This difference in attribution of benign and adversarial inputs can be used to detect adversarial examples. Such a defense approach is independent of training data and attack method, and we demonstrate its effectiveness on digital and physically realizable perturbations.