An Extension of Fano's Inequality for Characterizing Model Susceptibility to Membership Inference Attacks
Paper and Code
Sep 17, 2020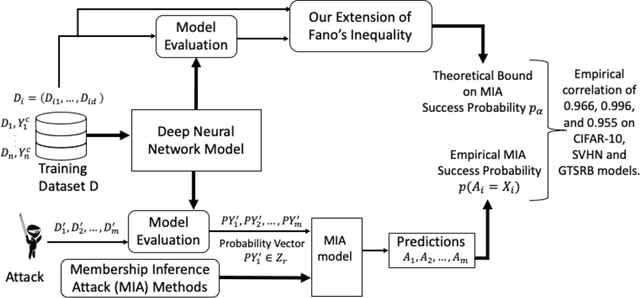
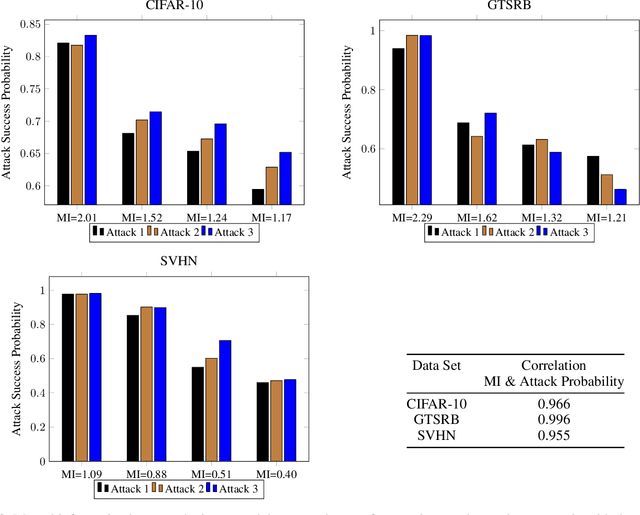
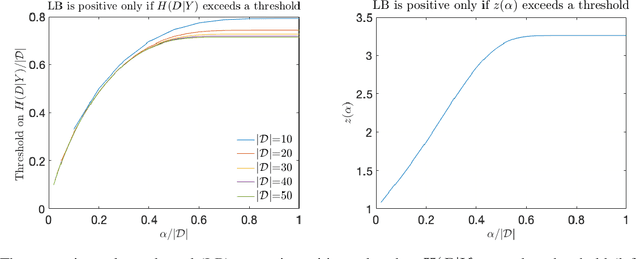
Deep neural networks have been shown to be vulnerable to membership inference attacks wherein the attacker aims to detect whether specific input data were used to train the model. These attacks can potentially leak private or proprietary data. We present a new extension of Fano's inequality and employ it to theoretically establish that the probability of success for a membership inference attack on a deep neural network can be bounded using the mutual information between its inputs and its activations. This enables the use of mutual information to measure the susceptibility of a DNN model to membership inference attacks. In our empirical evaluation, we show that the correlation between the mutual information and the susceptibility of the DNN model to membership inference attacks is 0.966, 0.996, and 0.955 for CIFAR-10, SVHN and GTSRB models, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge