Undermining Image and Text Classification Algorithms Using Adversarial Attacks

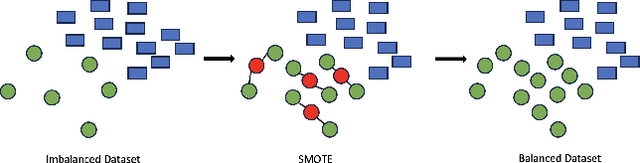
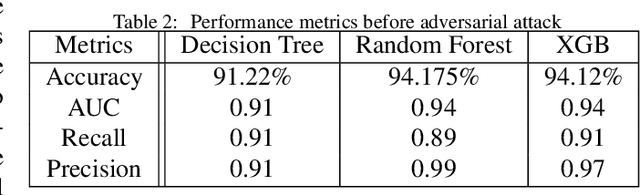
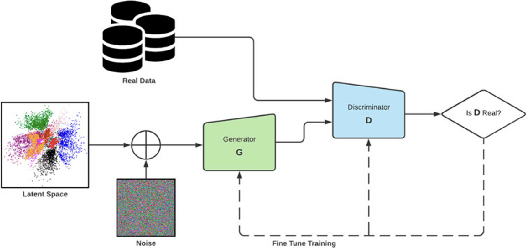
Machine learning models are prone to adversarial attacks, where inputs can be manipulated in order to cause misclassifications. While previous research has focused on techniques like Generative Adversarial Networks (GANs), there's limited exploration of GANs and Synthetic Minority Oversampling Technique (SMOTE) in text and image classification models to perform adversarial attacks. Our study addresses this gap by training various machine learning models and using GANs and SMOTE to generate additional data points aimed at attacking text classification models. Furthermore, we extend our investigation to face recognition models, training a Convolutional Neural Network(CNN) and subjecting it to adversarial attacks with fast gradient sign perturbations on key features identified by GradCAM, a technique used to highlight key image characteristics CNNs use in classification. Our experiments reveal a significant vulnerability in classification models. Specifically, we observe a 20 % decrease in accuracy for the top-performing text classification models post-attack, along with a 30 % decrease in facial recognition accuracy. This highlights the susceptibility of these models to manipulation of input data. Adversarial attacks not only compromise the security but also undermine the reliability of machine learning systems. By showcasing the impact of adversarial attacks on both text classification and face recognition models, our study underscores the urgent need for develop robust defenses against such vulnerabilities.

Plug-and-Play Unplugged: Optimization Free Reconstruction using Consensus Equilibrium

Regularized inversion methods for image reconstruction are used widely due to their tractability and ability to combine complex physical sensor models with useful regularity criteria. Such methods motivated the recently developed Plug-and-Play prior method, which provides a framework to use advanced denoising algorithms as regularizers in inversion. However, the need to formulate regularized inversion as the solution to an optimization problem limits the possible regularity conditions and physical sensor models. In this paper, we introduce Consensus Equilibrium (CE), which generalizes regularized inversion to include a much wider variety of both forward components and prior components without the need for either to be expressed with a cost function. CE is based on the solution of a set of equilibrium equations that balance data fit and regularity. In this framework, the problem of MAP estimation in regularized inversion is replaced by the problem of solving these equilibrium equations, which can be approached in multiple ways. The key contribution of CE is to provide a novel framework for fusing multiple heterogeneous models of physical sensors or models learned from data. We describe the derivation of the CE equations and prove that the solution of the CE equations generalizes the standard MAP estimate under appropriate circumstances. We also discuss algorithms for solving the CE equations, including ADMM with a novel form of preconditioning and Newton's method. We give examples to illustrate consensus equilibrium and the convergence properties of these algorithms and demonstrate this method on some toy problems and on a denoising example in which we use an array of convolutional neural network denoisers, none of which is tuned to match the noise level in a noisy image but which in consensus can achieve a better result than any of them individually.

Multi-resolution Data Fusion for Super-Resolution Electron Microscopy

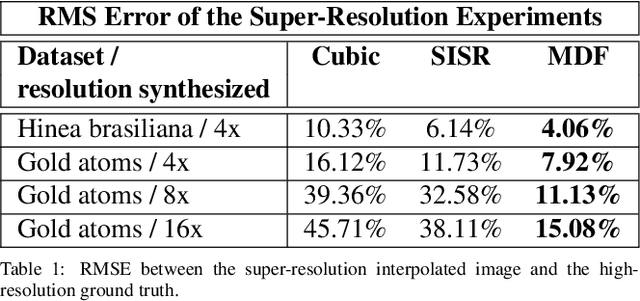
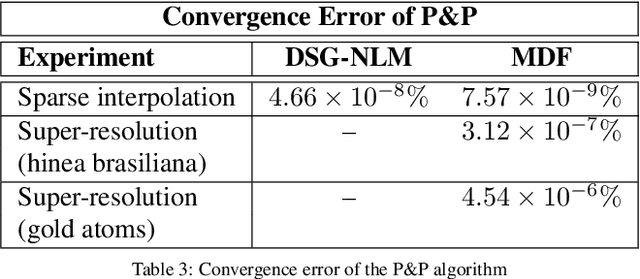
Perhaps surprisingly, the total electron microscopy (EM) data collected to date is less than a cubic millimeter. Consequently, there is an enormous demand in the materials and biological sciences to image at greater speed and lower dosage, while maintaining resolution. Traditional EM imaging based on homogeneous raster-order scanning severely limits the volume of high-resolution data that can be collected, and presents a fundamental limitation to understanding physical processes such as material deformation, crack propagation, and pyrolysis. We introduce a novel multi-resolution data fusion (MDF) method for super-resolution computational EM. Our method combines innovative data acquisition with novel algorithmic techniques to dramatically improve the resolution/volume/speed trade-off. The key to our approach is to collect the entire sample at low resolution, while simultaneously collecting a small fraction of data at high resolution. The high-resolution measurements are then used to create a material-specific patch-library that is used within the "plug-and-play" framework to dramatically improve super-resolution of the low-resolution data. We present results using FEI electron microscope data that demonstrate super-resolution factors of 4x, 8x, and 16x, while substantially maintaining high image quality and reducing dosage.

Plug-and-Play Priors for Bright Field Electron Tomography and Sparse Interpolation

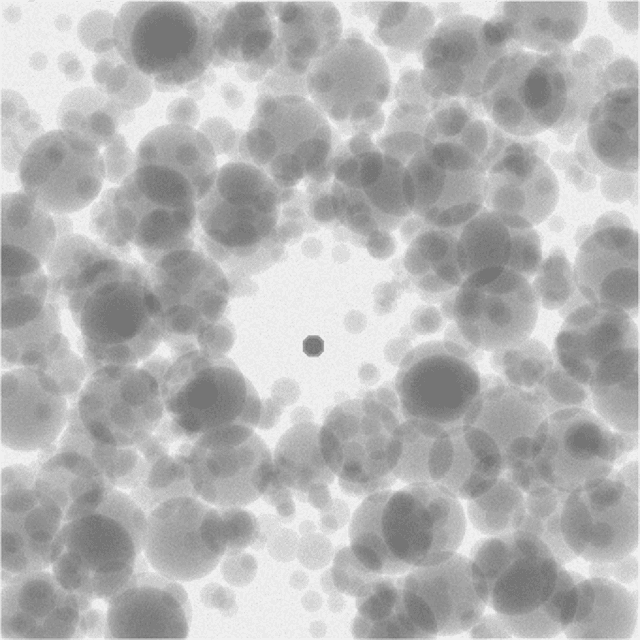
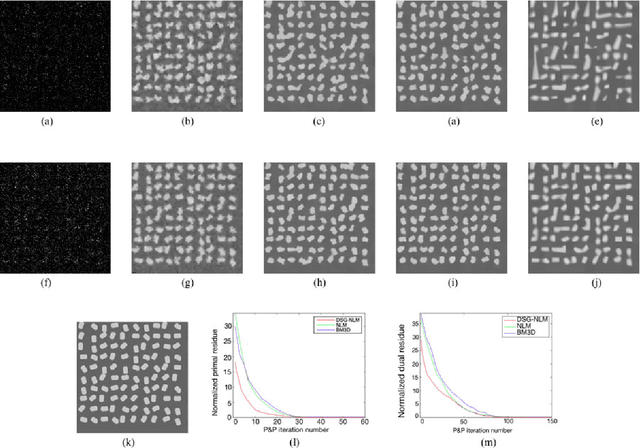
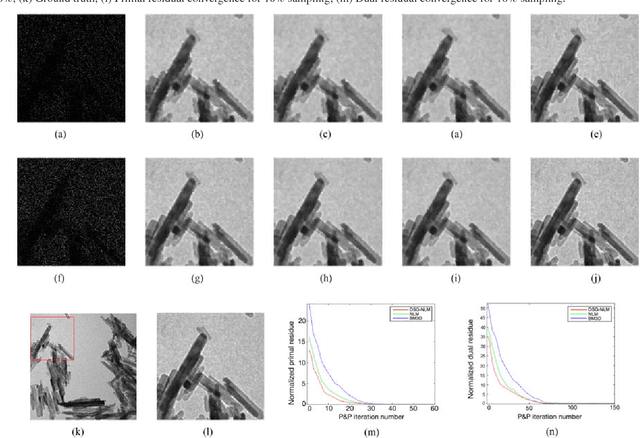
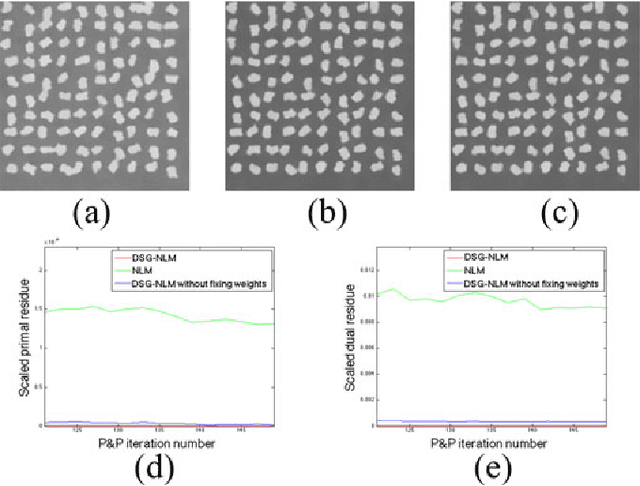
Many material and biological samples in scientific imaging are characterized by non-local repeating structures. These are studied using scanning electron microscopy and electron tomography. Sparse sampling of individual pixels in a 2D image acquisition geometry, or sparse sampling of projection images with large tilt increments in a tomography experiment, can enable high speed data acquisition and minimize sample damage caused by the electron beam. In this paper, we present an algorithm for electron tomographic reconstruction and sparse image interpolation that exploits the non-local redundancy in images. We adapt a framework, termed plug-and-play (P&P) priors, to solve these imaging problems in a regularized inversion setting. The power of the P&P approach is that it allows a wide array of modern denoising algorithms to be used as a "prior model" for tomography and image interpolation. We also present sufficient mathematical conditions that ensure convergence of the P&P approach, and we use these insights to design a new non-local means denoising algorithm. Finally, we demonstrate that the algorithm produces higher quality reconstructions on both simulated and real electron microscope data, along with improved convergence properties compared to other methods.