Multi-resolution Data Fusion for Super-Resolution Electron Microscopy

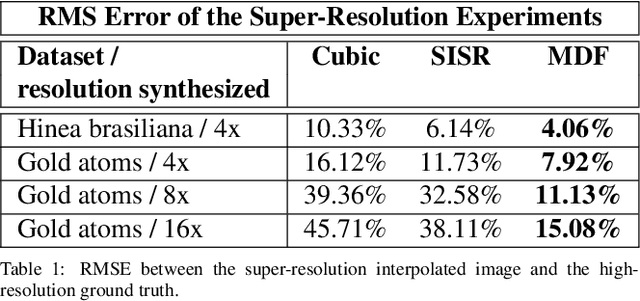
Perhaps surprisingly, the total electron microscopy (EM) data collected to date is less than a cubic millimeter. Consequently, there is an enormous demand in the materials and biological sciences to image at greater speed and lower dosage, while maintaining resolution. Traditional EM imaging based on homogeneous raster-order scanning severely limits the volume of high-resolution data that can be collected, and presents a fundamental limitation to understanding physical processes such as material deformation, crack propagation, and pyrolysis. We introduce a novel multi-resolution data fusion (MDF) method for super-resolution computational EM. Our method combines innovative data acquisition with novel algorithmic techniques to dramatically improve the resolution/volume/speed trade-off. The key to our approach is to collect the entire sample at low resolution, while simultaneously collecting a small fraction of data at high resolution. The high-resolution measurements are then used to create a material-specific patch-library that is used within the "plug-and-play" framework to dramatically improve super-resolution of the low-resolution data. We present results using FEI electron microscope data that demonstrate super-resolution factors of 4x, 8x, and 16x, while substantially maintaining high image quality and reducing dosage.

Plug-and-Play Priors for Bright Field Electron Tomography and Sparse Interpolation

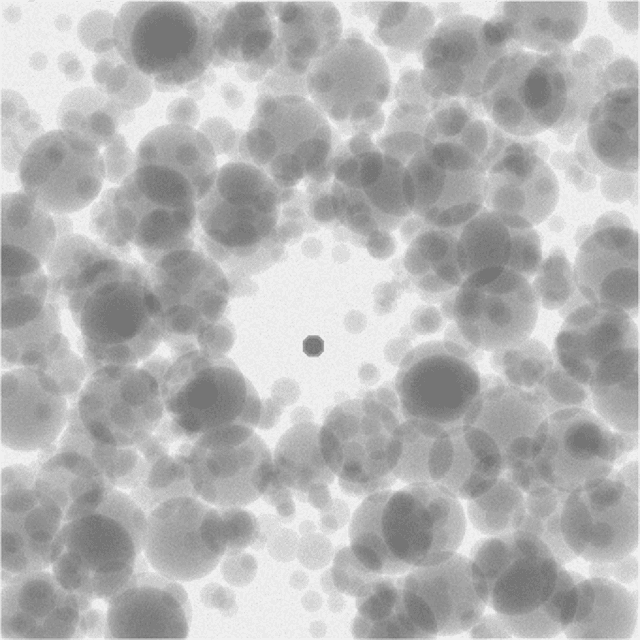
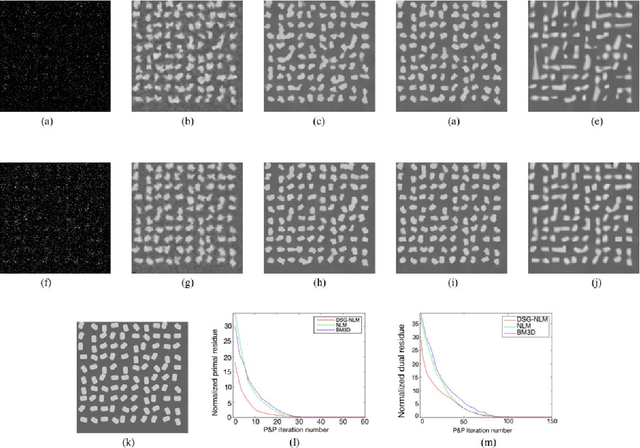
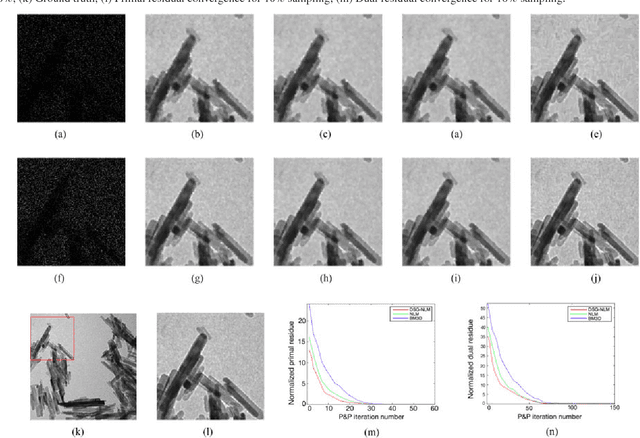
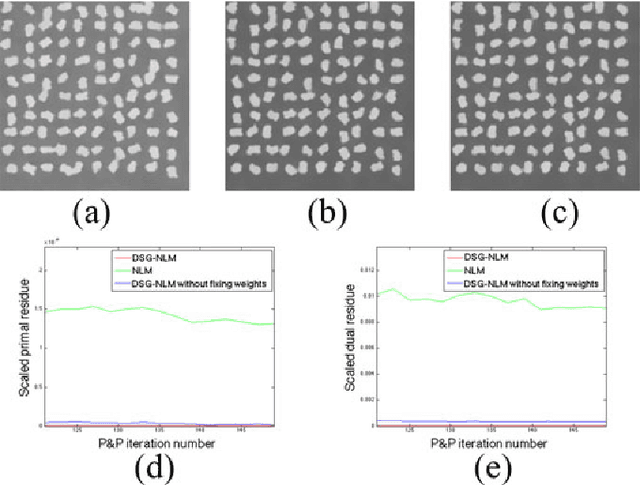
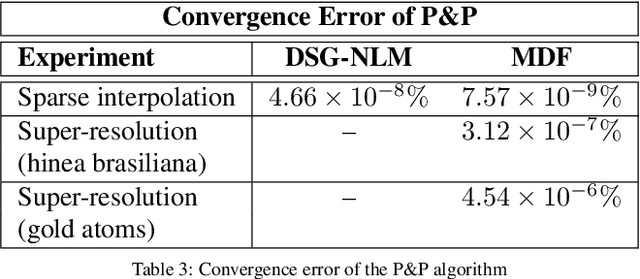
Many material and biological samples in scientific imaging are characterized by non-local repeating structures. These are studied using scanning electron microscopy and electron tomography. Sparse sampling of individual pixels in a 2D image acquisition geometry, or sparse sampling of projection images with large tilt increments in a tomography experiment, can enable high speed data acquisition and minimize sample damage caused by the electron beam. In this paper, we present an algorithm for electron tomographic reconstruction and sparse image interpolation that exploits the non-local redundancy in images. We adapt a framework, termed plug-and-play (P&P) priors, to solve these imaging problems in a regularized inversion setting. The power of the P&P approach is that it allows a wide array of modern denoising algorithms to be used as a "prior model" for tomography and image interpolation. We also present sufficient mathematical conditions that ensure convergence of the P&P approach, and we use these insights to design a new non-local means denoising algorithm. Finally, we demonstrate that the algorithm produces higher quality reconstructions on both simulated and real electron microscope data, along with improved convergence properties compared to other methods.