Plug-and-Play Priors for Bright Field Electron Tomography and Sparse Interpolation
Paper and Code
Dec 23, 2015
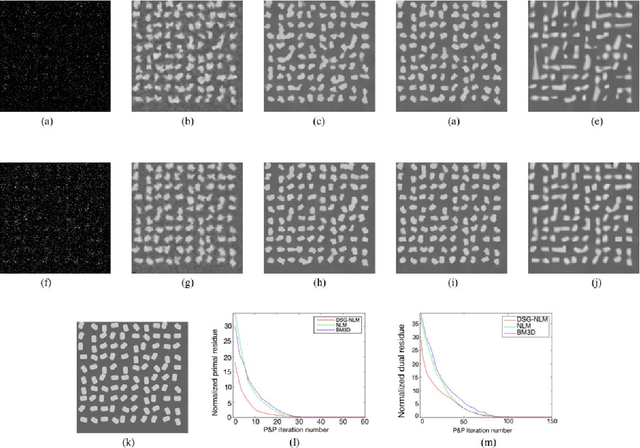
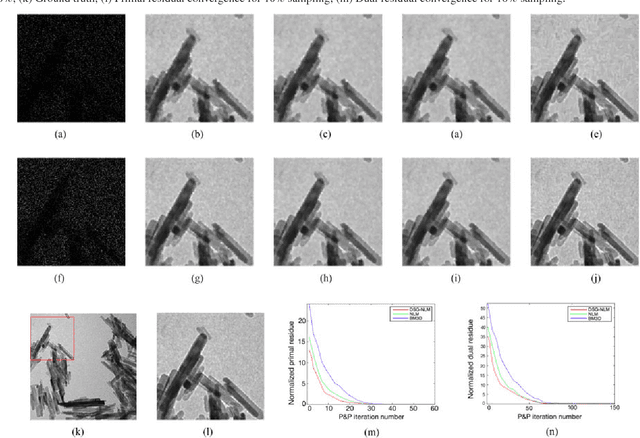
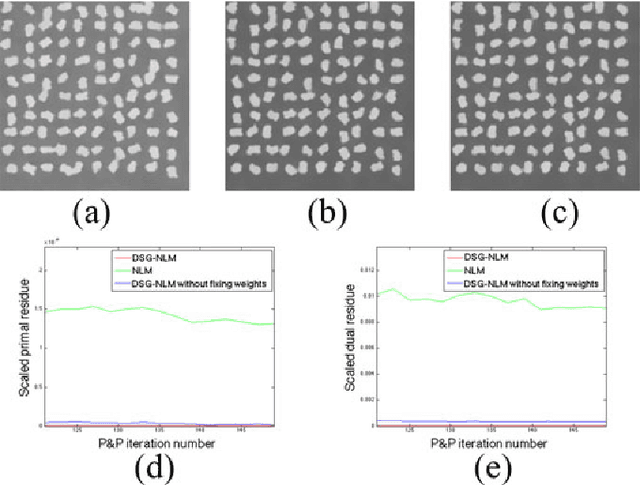
Many material and biological samples in scientific imaging are characterized by non-local repeating structures. These are studied using scanning electron microscopy and electron tomography. Sparse sampling of individual pixels in a 2D image acquisition geometry, or sparse sampling of projection images with large tilt increments in a tomography experiment, can enable high speed data acquisition and minimize sample damage caused by the electron beam. In this paper, we present an algorithm for electron tomographic reconstruction and sparse image interpolation that exploits the non-local redundancy in images. We adapt a framework, termed plug-and-play (P&P) priors, to solve these imaging problems in a regularized inversion setting. The power of the P&P approach is that it allows a wide array of modern denoising algorithms to be used as a "prior model" for tomography and image interpolation. We also present sufficient mathematical conditions that ensure convergence of the P&P approach, and we use these insights to design a new non-local means denoising algorithm. Finally, we demonstrate that the algorithm produces higher quality reconstructions on both simulated and real electron microscope data, along with improved convergence properties compared to other methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge