Generalizing Constraint Models in Constraint Acquisition

Constraint Acquisition (CA) aims to widen the use of constraint programming by assisting users in the modeling process. However, most CA methods suffer from a significant drawback: they learn a single set of individual constraints for a specific problem instance, but cannot generalize these constraints to the parameterized constraint specifications of the problem. In this paper, we address this limitation by proposing GenCon, a novel approach to learn parameterized constraint models capable of modeling varying instances of the same problem. To achieve this generalization, we make use of statistical learning techniques at the level of individual constraints. Specifically, we propose to train a classifier to predict, for any possible constraint and parameterization, whether the constraint belongs to the problem. We then show how, for some classes of classifiers, we can extract decision rules to construct interpretable constraint specifications. This enables the generation of ground constraints for any parameter instantiation. Additionally, we present a generate-and-test approach that can be used with any classifier, to generate the ground constraints on the fly. Our empirical results demonstrate that our approach achieves high accuracy and is robust to noise in the input instances.

Optimizing Quantile-based Trading Strategies in Electricity Arbitrage

Efficiently integrating renewable resources into electricity markets is vital for addressing the challenges of matching real-time supply and demand while reducing the significant energy wastage resulting from curtailments. To address this challenge effectively, the incorporation of storage devices can enhance the reliability and efficiency of the grid, improving market liquidity and reducing price volatility. In short-term electricity markets, participants navigate numerous options, each presenting unique challenges and opportunities, underscoring the critical role of the trading strategy in maximizing profits. This study delves into the optimization of day-ahead and balancing market trading, leveraging quantile-based forecasts. Employing three trading approaches with practical constraints, our research enhances forecast assessment, increases trading frequency, and employs flexible timestamp orders. Our findings underscore the profit potential of simultaneous participation in both day-ahead and balancing markets, especially with larger battery storage systems; despite increased costs and narrower profit margins associated with higher-volume trading, the implementation of high-frequency strategies plays a significant role in maximizing profits and addressing market challenges. Finally, we modelled four commercial battery storage systems and evaluated their economic viability through a scenario analysis, with larger batteries showing a shorter return on investment.

Electricity Price Forecasting in the Irish Balancing Market

Short-term electricity markets are becoming more relevant due to less-predictable renewable energy sources, attracting considerable attention from the industry. The balancing market is the closest to real-time and the most volatile among them. Its price forecasting literature is limited, inconsistent and outdated, with few deep learning attempts and no public dataset. This work applies to the Irish balancing market a variety of price prediction techniques proven successful in the widely studied day-ahead market. We compare statistical, machine learning, and deep learning models using a framework that investigates the impact of different training sizes. The framework defines hyperparameters and calibration settings; the dataset and models are made public to ensure reproducibility and to be used as benchmarks for future works. An extensive numerical study shows that well-performing models in the day-ahead market do not perform well in the balancing one, highlighting that these markets are fundamentally different constructs. The best model is LEAR, a statistical approach based on LASSO, which outperforms more complex and computationally demanding approaches.

A hybrid estimation of distribution algorithm for joint stratification and sample allocation

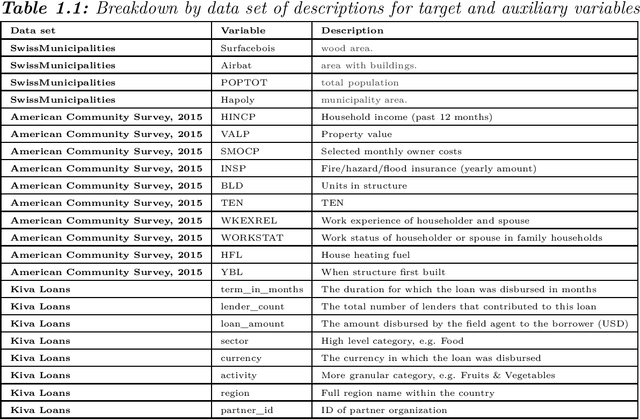
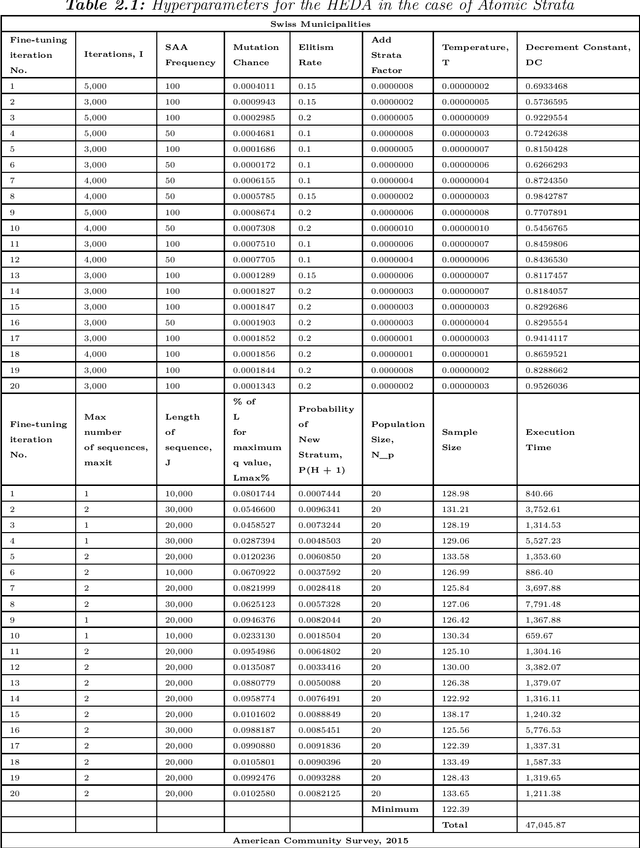
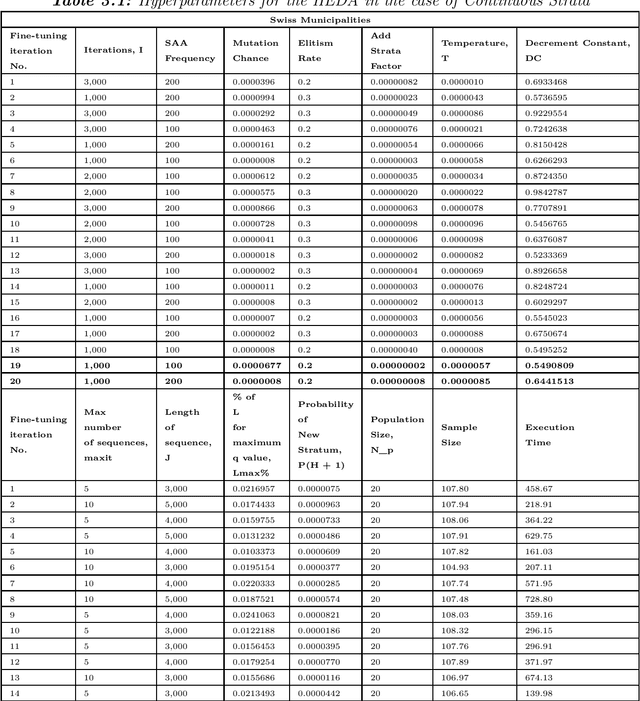
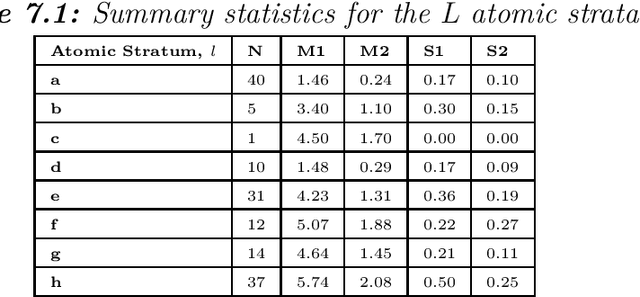
In this study we propose a hybrid estimation of distribution algorithm (HEDA) to solve the joint stratification and sample allocation problem. This is a complex problem in which each the quality of each stratification from the set of all possible stratifications is measured its optimal sample allocation. EDAs are stochastic black-box optimization algorithms which can be used to estimate, build and sample probability models in the search for an optimal stratification. In this paper we enhance the exploitation properties of the EDA by adding a simulated annealing algorithm to make it a hybrid EDA. Results of empirical comparisons for atomic and continuous strata show that the HEDA attains the bests results found so far when compared to benchmark tests on the same data using a grouping genetic algorithm, simulated annealing algorithm or hill-climbing algorithm. However, the execution times and total execution are, in general, higher for the HEDA.

Combining K-means type algorithms with Hill Climbing for Joint Stratification and Sample Allocation Designs

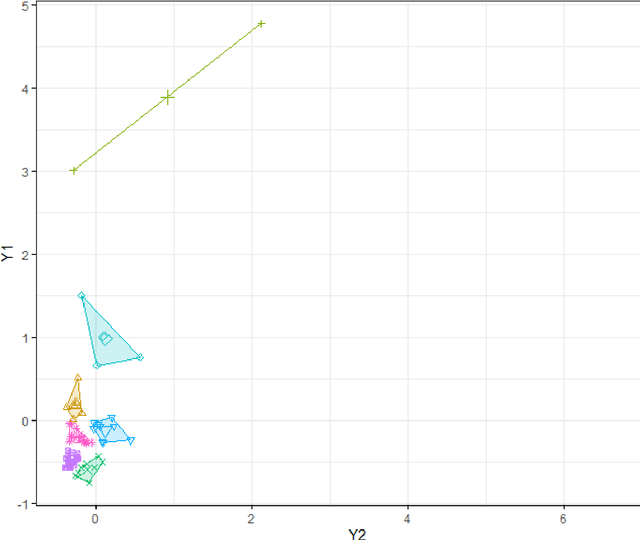
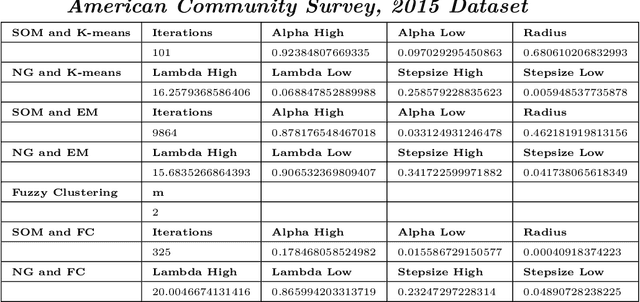
In this paper we combine the k-means and/or k-means type algorithms with a hill climbing algorithm in stages to solve the joint stratification and sample allocation problem. This is a combinatorial optimisation problem in which we search for the optimal stratification from the set of all possible stratifications of basic strata. Each stratification being a solution the quality of which is measured by its cost. This problem is intractable for larger sets. Furthermore evaluating the cost of each solution is expensive. A number of heuristic algorithms have already been developed to solve this problem with the aim of finding acceptable solutions in reasonable computation times. However, the heuristics for these algorithms need to be trained in order to optimise performance in each instance. We compare the above multi-stage combination of algorithms with three recent algorithms and report the solution costs, evaluation times and training times. The multi-stage combinations generally compare well with the recent algorithms both in the case of atomic and continuous strata and provide the survey designer with a greater choice of algorithms to choose from.

A Simulated Annealing Algorithm for Joint Stratification and Sample Allocation Designs

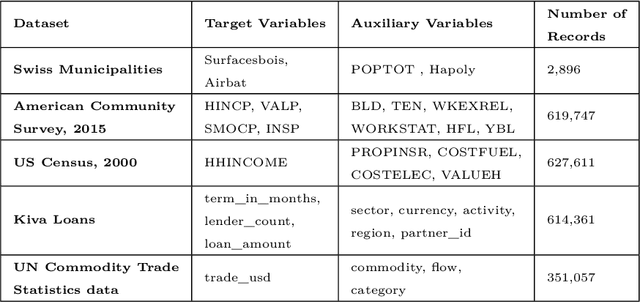
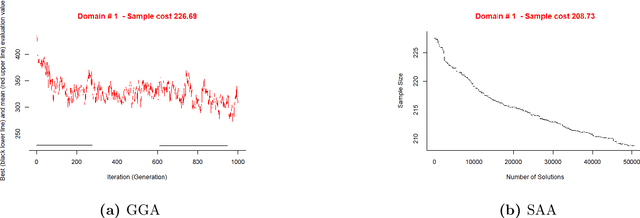
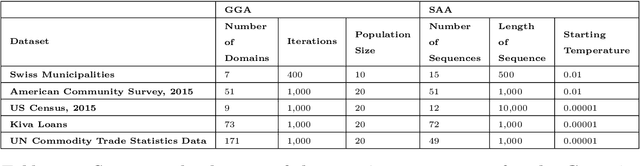
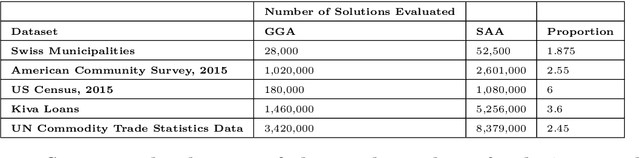
This study combined simulated annealing with delta evaluation to solve the joint stratification and sample allocation problem. In this problem, atomic strata are partitioned into mutually exclusive and collectively exhaustive strata. Each stratification is a solution, the quality of which is measured by its cost. The Bell number of possible solutions is enormous for even a moderate number of atomic strata and an additional layer of complexity is added with the evaluation time of each solution. Many larger scale combinatorial optimisation problems cannot be solved to optimality because the search for an optimum solution requires a prohibitive amount of computation time; a number of local search heuristic algorithms have been designed for this problem but these can become trapped in local minima preventing any further improvements. We add to the existing suite of local search algorithms with a simulated annealing algorithm that allows for an escape from local minima and uses delta evaluation to exploit the similarity between consecutive solutions and thereby reduce the evaluation time.

Denoising Dictionary Learning Against Adversarial Perturbations

We propose denoising dictionary learning (DDL), a simple yet effective technique as a protection measure against adversarial perturbations. We examined denoising dictionary learning on MNIST and CIFAR10 perturbed under two different perturbation techniques, fast gradient sign (FGSM) and jacobian saliency maps (JSMA). We evaluated it against five different deep neural networks (DNN) representing the building blocks of most recent architectures indicating a successive progression of model complexity of each other. We show that each model tends to capture different representations based on their architecture. For each model we recorded its accuracy both on the perturbed test data previously misclassified with high confidence and on the denoised one after the reconstruction using dictionary learning. The reconstruction quality of each data point is assessed by means of PSNR (Peak Signal to Noise Ratio) and Structure Similarity Index (SSI). We show that after applying (DDL) the reconstruction of the original data point from a noisy

Declarative Statistics

In this work we introduce declarative statistics, a suite of declarative modelling tools for statistical analysis. Statistical constraints represent the key building block of declarative statistics. First, we introduce a range of relevant counting and matrix constraints and associated decompositions, some of which novel, that are instrumental in the design of statistical constraints. Second, we introduce a selection of novel statistical constraints and associated decompositions, which constitute a self-contained toolbox that can be used to tackle a wide range of problems typically encountered by statisticians. Finally, we deploy these statistical constraints to a wide range of application areas drawn from classical statistics and we contrast our framework against established practices.

Stochastic Constraint Programming as Reinforcement Learning

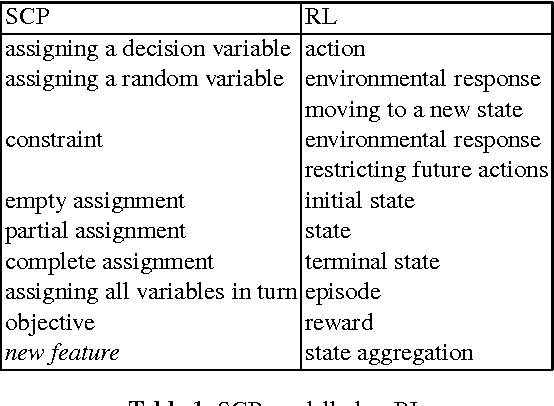
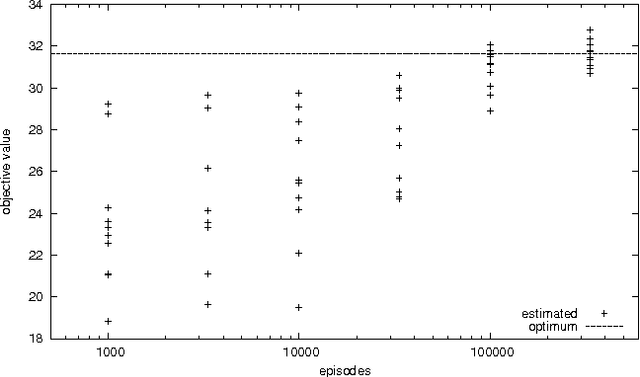
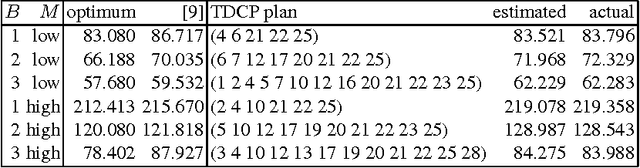
Stochastic Constraint Programming (SCP) is an extension of Constraint Programming (CP) used for modelling and solving problems involving constraints and uncertainty. SCP inherits excellent modelling abilities and filtering algorithms from CP, but so far it has not been applied to large problems. Reinforcement Learning (RL) extends Dynamic Programming to large stochastic problems, but is problem-specific and has no generic solvers. We propose a hybrid combining the scalability of RL with the modelling and constraint filtering methods of CP. We implement a prototype in a CP system and demonstrate its usefulness on SCP problems.

The BIN_COUNTS Constraint: Filtering and Applications

We introduce the BIN_COUNTS constraint, which deals with the problem of counting the number of decision variables in a set which are assigned values that lie in given bins. We illustrate a decomposition and a filtering algorithm that achieves generalised arc consistency. We contrast the filtering power of these two approaches and we discuss a number of applications. We show that BIN_COUNTS can be employed to develop a decomposition for the $\chi^2$ test constraint, a new statistical constraint that we introduce in this work. We also show how this new constraint can be employed in the context of the Balanced Academic Curriculum Problem and of the Balanced Nursing Workload Problem. For both these problems we carry out numerical studies involving our reformulations. Finally, we present a further application of the $\chi^2$ test constraint in the context of confidence interval analysis.