The importance of visual modelling languages in generative software engineering

Multimodal GPTs represent a watershed in the interplay between Software Engineering and Generative Artificial Intelligence. GPT-4 accepts image and text inputs, rather than simply natural language. We investigate relevant use cases stemming from these enhanced capabilities of GPT-4. To the best of our knowledge, no other work has investigated similar use cases involving Software Engineering tasks carried out via multimodal GPTs prompted with a mix of diagrams and natural language.

jsdp: a Java Stochastic Dynamic Programming Library

Stochastic Programming is a framework for modelling and solving problems of decision making under uncertainty. Stochastic Dynamic Programming is a branch of Stochastic Programming that takes a "functional equation" approach to the discovery of optimal policies. By leveraging constructs - lambda expressions, functional interfaces, collections and aggregate operators - implemented in Java to operationalise the MapReduce framework, jsdp provides a general purpose library for modelling and solving Stochastic Dynamic Programs.

Declarative Statistics

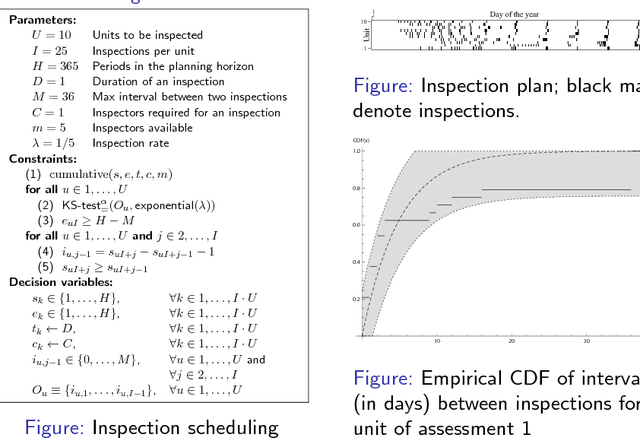
In this work we introduce declarative statistics, a suite of declarative modelling tools for statistical analysis. Statistical constraints represent the key building block of declarative statistics. First, we introduce a range of relevant counting and matrix constraints and associated decompositions, some of which novel, that are instrumental in the design of statistical constraints. Second, we introduce a selection of novel statistical constraints and associated decompositions, which constitute a self-contained toolbox that can be used to tackle a wide range of problems typically encountered by statisticians. Finally, we deploy these statistical constraints to a wide range of application areas drawn from classical statistics and we contrast our framework against established practices.

Stochastic Constraint Programming as Reinforcement Learning

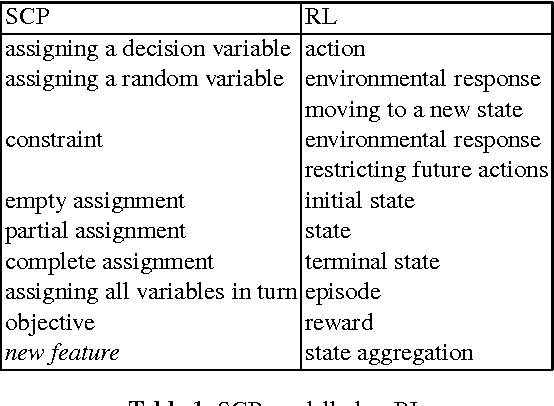
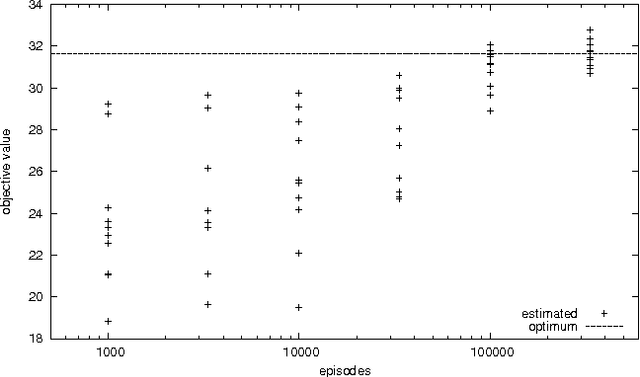
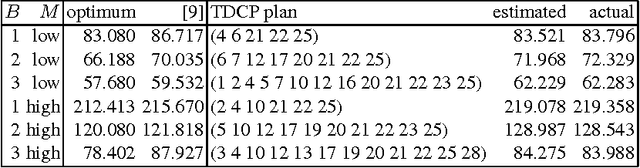
Stochastic Constraint Programming (SCP) is an extension of Constraint Programming (CP) used for modelling and solving problems involving constraints and uncertainty. SCP inherits excellent modelling abilities and filtering algorithms from CP, but so far it has not been applied to large problems. Reinforcement Learning (RL) extends Dynamic Programming to large stochastic problems, but is problem-specific and has no generic solvers. We propose a hybrid combining the scalability of RL with the modelling and constraint filtering methods of CP. We implement a prototype in a CP system and demonstrate its usefulness on SCP problems.

The BIN_COUNTS Constraint: Filtering and Applications

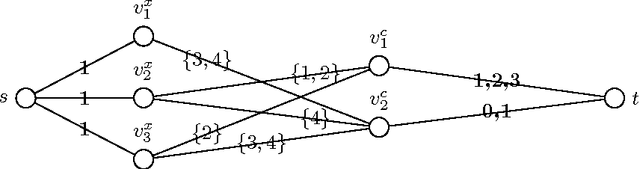
We introduce the BIN_COUNTS constraint, which deals with the problem of counting the number of decision variables in a set which are assigned values that lie in given bins. We illustrate a decomposition and a filtering algorithm that achieves generalised arc consistency. We contrast the filtering power of these two approaches and we discuss a number of applications. We show that BIN_COUNTS can be employed to develop a decomposition for the $\chi^2$ test constraint, a new statistical constraint that we introduce in this work. We also show how this new constraint can be employed in the context of the Balanced Academic Curriculum Problem and of the Balanced Nursing Workload Problem. For both these problems we carry out numerical studies involving our reformulations. Finally, we present a further application of the $\chi^2$ test constraint in the context of confidence interval analysis.

Confidence-based Reasoning in Stochastic Constraint Programming

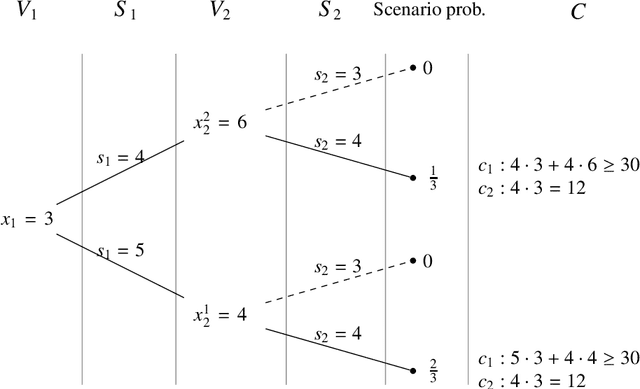
In this work we introduce a novel approach, based on sampling, for finding assignments that are likely to be solutions to stochastic constraint satisfaction problems and constraint optimisation problems. Our approach reduces the size of the original problem being analysed; by solving this reduced problem, with a given confidence probability, we obtain assignments that satisfy the chance constraints in the original model within prescribed error tolerance thresholds. To achieve this, we blend concepts from stochastic constraint programming and statistics. We discuss both exact and approximate variants of our method. The framework we introduce can be immediately employed in concert with existing approaches for solving stochastic constraint programs. A thorough computational study on a number of stochastic combinatorial optimisation problems demonstrates the effectiveness of our approach.

Statistical Constraints

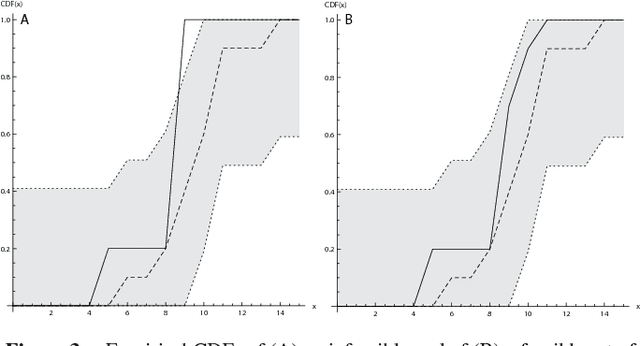
We introduce statistical constraints, a declarative modelling tool that links statistics and constraint programming. We discuss two statistical constraints and some associated filtering algorithms. Finally, we illustrate applications to standard problems encountered in statistics and to a novel inspection scheduling problem in which the aim is to find inspection plans with desirable statistical properties.