Stochastic Constraint Programming as Reinforcement Learning

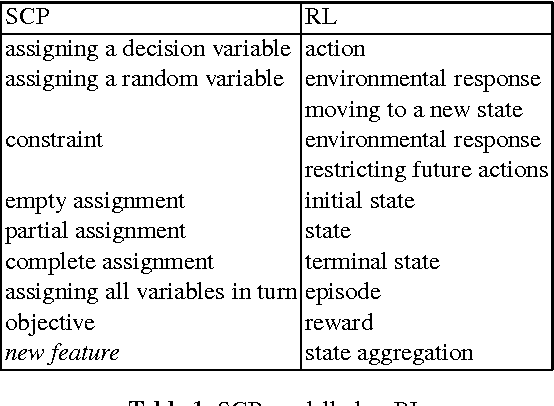
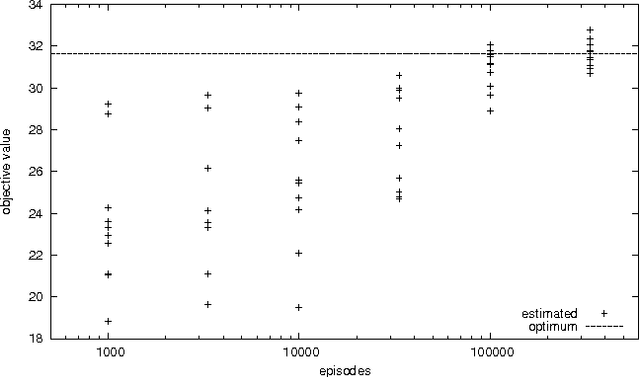
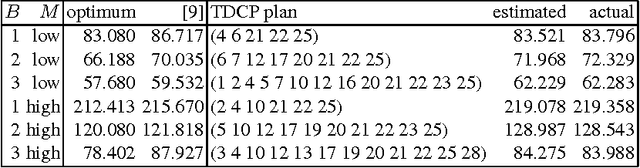
Stochastic Constraint Programming (SCP) is an extension of Constraint Programming (CP) used for modelling and solving problems involving constraints and uncertainty. SCP inherits excellent modelling abilities and filtering algorithms from CP, but so far it has not been applied to large problems. Reinforcement Learning (RL) extends Dynamic Programming to large stochastic problems, but is problem-specific and has no generic solvers. We propose a hybrid combining the scalability of RL with the modelling and constraint filtering methods of CP. We implement a prototype in a CP system and demonstrate its usefulness on SCP problems.

The BIN_COUNTS Constraint: Filtering and Applications

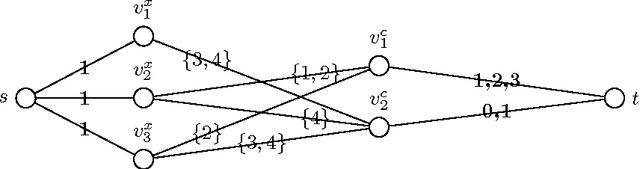
We introduce the BIN_COUNTS constraint, which deals with the problem of counting the number of decision variables in a set which are assigned values that lie in given bins. We illustrate a decomposition and a filtering algorithm that achieves generalised arc consistency. We contrast the filtering power of these two approaches and we discuss a number of applications. We show that BIN_COUNTS can be employed to develop a decomposition for the $\chi^2$ test constraint, a new statistical constraint that we introduce in this work. We also show how this new constraint can be employed in the context of the Balanced Academic Curriculum Problem and of the Balanced Nursing Workload Problem. For both these problems we carry out numerical studies involving our reformulations. Finally, we present a further application of the $\chi^2$ test constraint in the context of confidence interval analysis.

Scenario-based Stochastic Constraint Programming

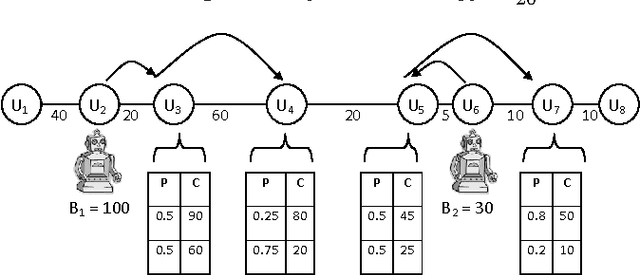
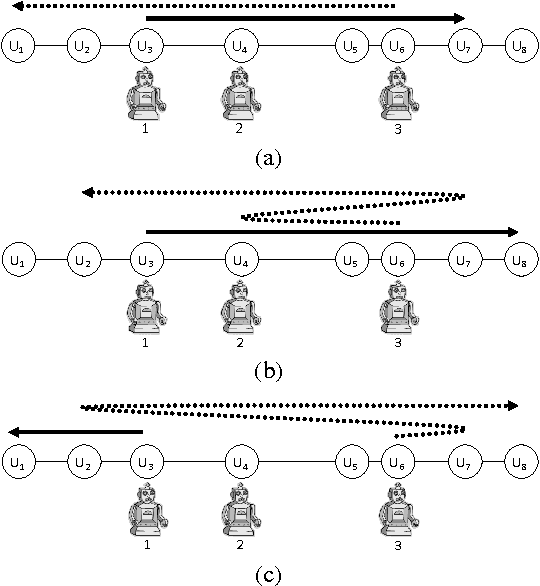
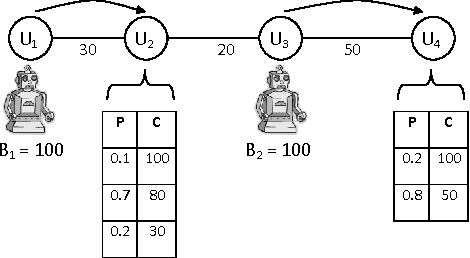
To model combinatorial decision problems involving uncertainty and probability, we extend the stochastic constraint programming framework proposed in [Walsh, 2002] along a number of important dimensions (e.g. to multiple chance constraints and to a range of new objectives). We also provide a new (but equivalent) semantics based on scenarios. Using this semantics, we can compile stochastic constraint programs down into conventional (nonstochastic) constraint programs. This allows us to exploit the full power of existing constraint solvers. We have implemented this framework for decision making under uncertainty in stochastic OPL, a language which is based on the OPL constraint modelling language [Hentenryck et al., 1999]. To illustrate the potential of this framework, we model a wide range of problems in areas as diverse as finance, agriculture and production.