A hybrid estimation of distribution algorithm for joint stratification and sample allocation

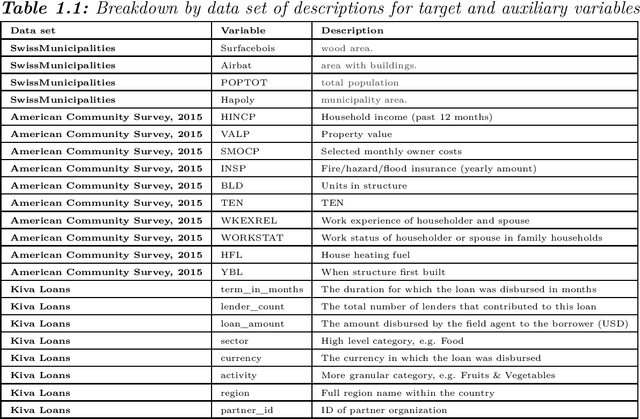
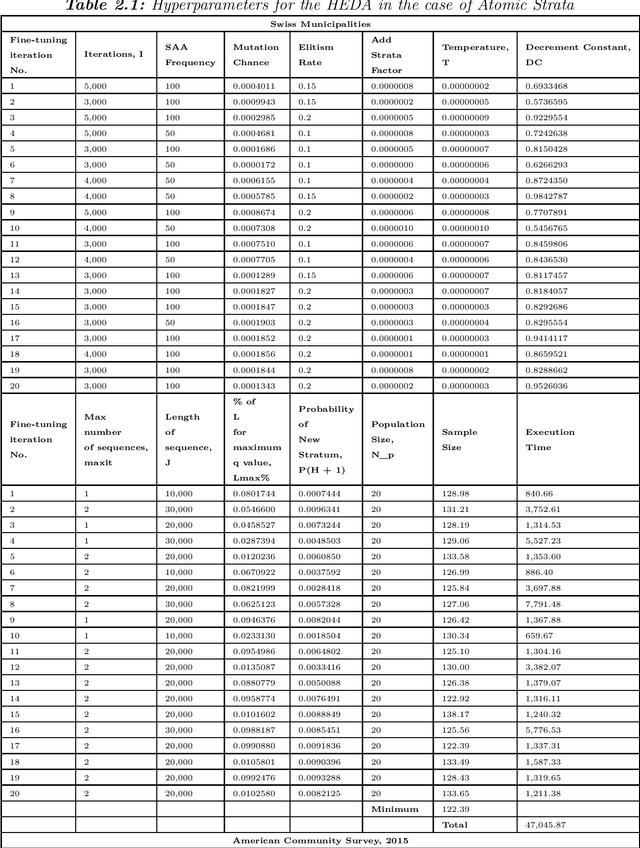
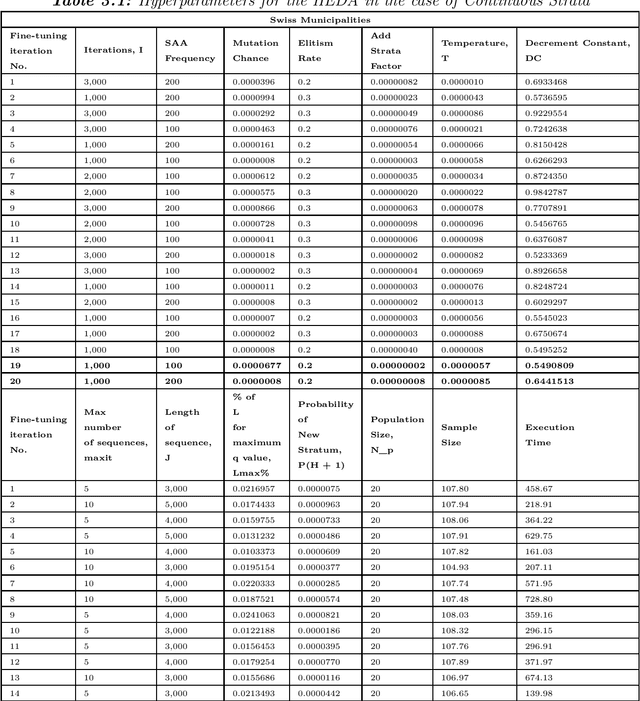
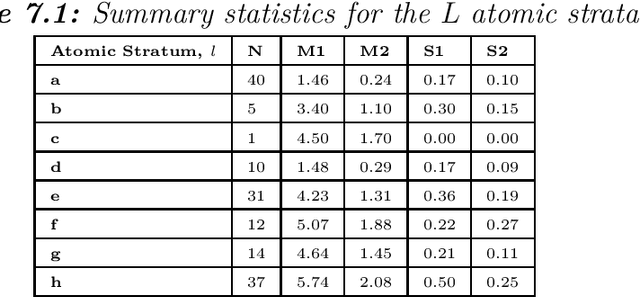
In this study we propose a hybrid estimation of distribution algorithm (HEDA) to solve the joint stratification and sample allocation problem. This is a complex problem in which each the quality of each stratification from the set of all possible stratifications is measured its optimal sample allocation. EDAs are stochastic black-box optimization algorithms which can be used to estimate, build and sample probability models in the search for an optimal stratification. In this paper we enhance the exploitation properties of the EDA by adding a simulated annealing algorithm to make it a hybrid EDA. Results of empirical comparisons for atomic and continuous strata show that the HEDA attains the bests results found so far when compared to benchmark tests on the same data using a grouping genetic algorithm, simulated annealing algorithm or hill-climbing algorithm. However, the execution times and total execution are, in general, higher for the HEDA.

Combining K-means type algorithms with Hill Climbing for Joint Stratification and Sample Allocation Designs

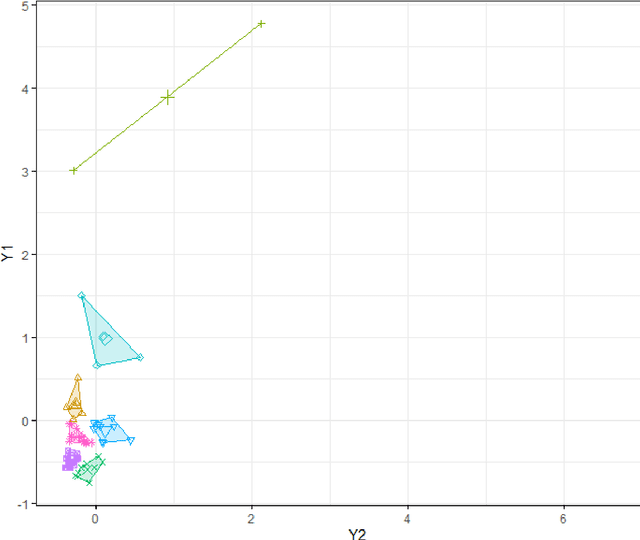
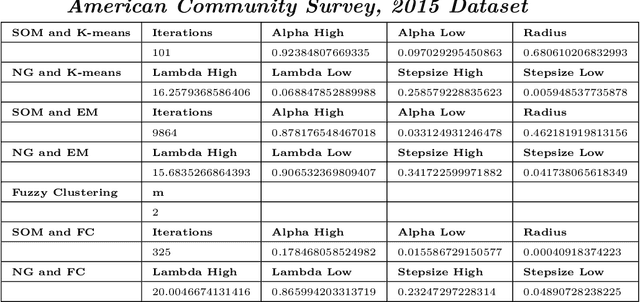
In this paper we combine the k-means and/or k-means type algorithms with a hill climbing algorithm in stages to solve the joint stratification and sample allocation problem. This is a combinatorial optimisation problem in which we search for the optimal stratification from the set of all possible stratifications of basic strata. Each stratification being a solution the quality of which is measured by its cost. This problem is intractable for larger sets. Furthermore evaluating the cost of each solution is expensive. A number of heuristic algorithms have already been developed to solve this problem with the aim of finding acceptable solutions in reasonable computation times. However, the heuristics for these algorithms need to be trained in order to optimise performance in each instance. We compare the above multi-stage combination of algorithms with three recent algorithms and report the solution costs, evaluation times and training times. The multi-stage combinations generally compare well with the recent algorithms both in the case of atomic and continuous strata and provide the survey designer with a greater choice of algorithms to choose from.

A Simulated Annealing Algorithm for Joint Stratification and Sample Allocation Designs

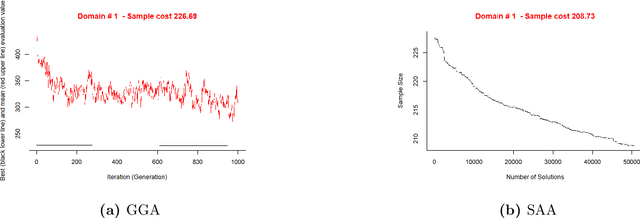
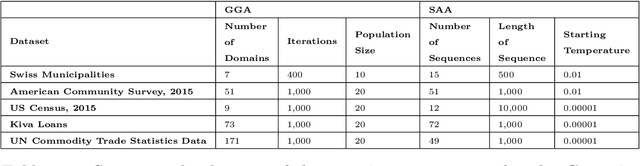
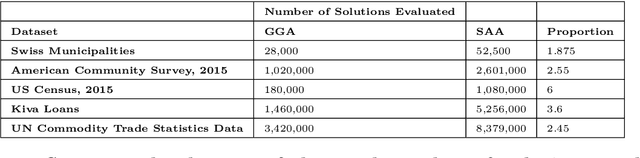
This study combined simulated annealing with delta evaluation to solve the joint stratification and sample allocation problem. In this problem, atomic strata are partitioned into mutually exclusive and collectively exhaustive strata. Each stratification is a solution, the quality of which is measured by its cost. The Bell number of possible solutions is enormous for even a moderate number of atomic strata and an additional layer of complexity is added with the evaluation time of each solution. Many larger scale combinatorial optimisation problems cannot be solved to optimality because the search for an optimum solution requires a prohibitive amount of computation time; a number of local search heuristic algorithms have been designed for this problem but these can become trapped in local minima preventing any further improvements. We add to the existing suite of local search algorithms with a simulated annealing algorithm that allows for an escape from local minima and uses delta evaluation to exploit the similarity between consecutive solutions and thereby reduce the evaluation time.

Declarative Statistics

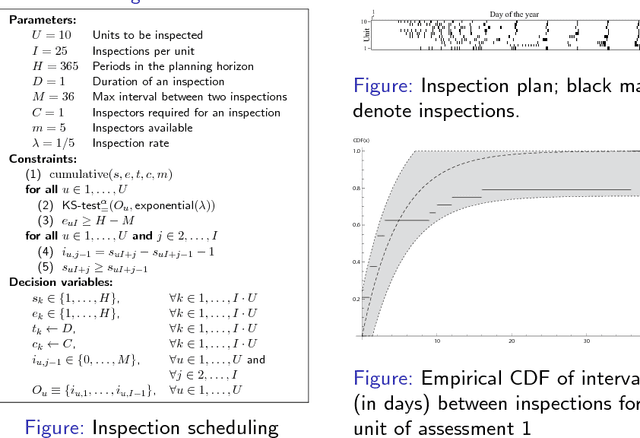
In this work we introduce declarative statistics, a suite of declarative modelling tools for statistical analysis. Statistical constraints represent the key building block of declarative statistics. First, we introduce a range of relevant counting and matrix constraints and associated decompositions, some of which novel, that are instrumental in the design of statistical constraints. Second, we introduce a selection of novel statistical constraints and associated decompositions, which constitute a self-contained toolbox that can be used to tackle a wide range of problems typically encountered by statisticians. Finally, we deploy these statistical constraints to a wide range of application areas drawn from classical statistics and we contrast our framework against established practices.

Confidence-based Reasoning in Stochastic Constraint Programming

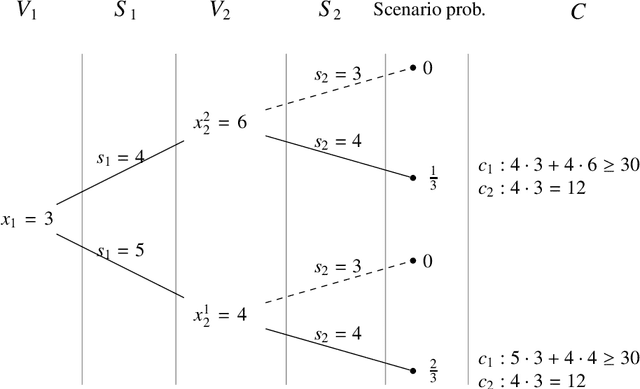
In this work we introduce a novel approach, based on sampling, for finding assignments that are likely to be solutions to stochastic constraint satisfaction problems and constraint optimisation problems. Our approach reduces the size of the original problem being analysed; by solving this reduced problem, with a given confidence probability, we obtain assignments that satisfy the chance constraints in the original model within prescribed error tolerance thresholds. To achieve this, we blend concepts from stochastic constraint programming and statistics. We discuss both exact and approximate variants of our method. The framework we introduce can be immediately employed in concert with existing approaches for solving stochastic constraint programs. A thorough computational study on a number of stochastic combinatorial optimisation problems demonstrates the effectiveness of our approach.

Statistical Constraints

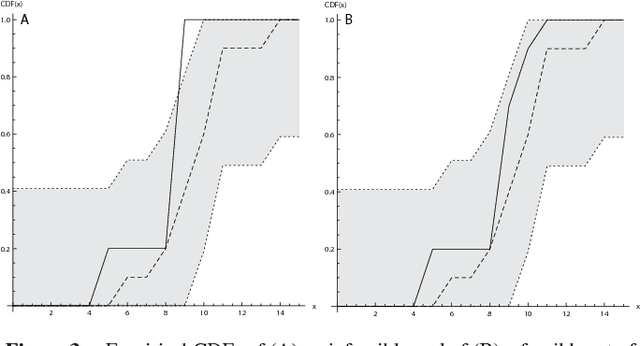
We introduce statistical constraints, a declarative modelling tool that links statistics and constraint programming. We discuss two statistical constraints and some associated filtering algorithms. Finally, we illustrate applications to standard problems encountered in statistics and to a novel inspection scheduling problem in which the aim is to find inspection plans with desirable statistical properties.

Stochastic Constraint Programming: A Scenario-Based Approach

To model combinatorial decision problems involving uncertainty and probability, we introduce scenario based stochastic constraint programming. Stochastic constraint programs contain both decision variables, which we can set, and stochastic variables, which follow a discrete probability distribution. We provide a semantics for stochastic constraint programs based on scenario trees. Using this semantics, we can compile stochastic constraint programs down into conventional (non-stochastic) constraint programs. This allows us to exploit the full power of existing constraint solvers. We have implemented this framework for decision making under uncertainty in stochastic OPL, a language which is based on the OPL constraint modelling language [Hentenryck et al., 1999]. To illustrate the potential of this framework, we model a wide range of problems in areas as diverse as portfolio diversification, agricultural planning and production/inventory management.