Dynamic Question Ordering in Online Surveys

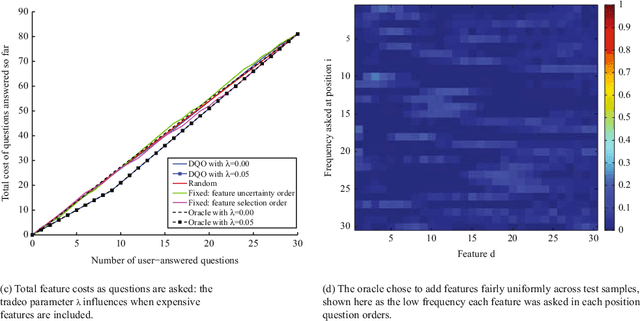
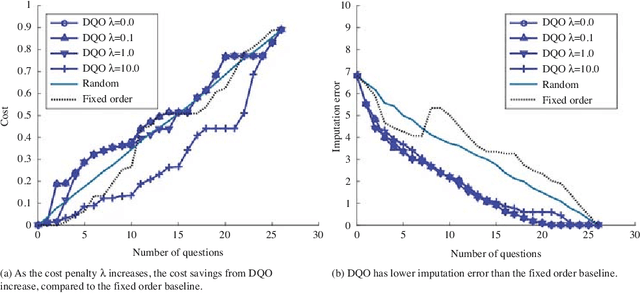
Online surveys have the potential to support adaptive questions, where later questions depend on earlier responses. Past work has taken a rule-based approach, uniformly across all respondents. We envision a richer interpretation of adaptive questions, which we call dynamic question ordering (DQO), where question order is personalized. Such an approach could increase engagement, and therefore response rate, as well as imputation quality. We present a DQO framework to improve survey completion and imputation. In the general survey-taking setting, we want to maximize survey completion, and so we focus on ordering questions to engage the respondent and collect hopefully all information, or at least the information that most characterizes the respondent, for accurate imputations. In another scenario, our goal is to provide a personalized prediction. Since it is possible to give reasonable predictions with only a subset of questions, we are not concerned with motivating users to answer all questions. Instead, we want to order questions to get information that reduces prediction uncertainty, while not being too burdensome. We illustrate this framework with an example of providing energy estimates to prospective tenants. We also discuss DQO for national surveys and consider connections between our statistics-based question-ordering approach and cognitive survey methodology.

On-Average KL-Privacy and its equivalence to Generalization for Max-Entropy Mechanisms

We define On-Average KL-Privacy and present its properties and connections to differential privacy, generalization and information-theoretic quantities including max-information and mutual information. The new definition significantly weakens differential privacy, while preserving its minimalistic design features such as composition over small group and multiple queries as well as closeness to post-processing. Moreover, we show that On-Average KL-Privacy is **equivalent** to generalization for a large class of commonly-used tools in statistics and machine learning that samples from Gibbs distributions---a class of distributions that arises naturally from the maximum entropy principle. In addition, a byproduct of our analysis yields a lower bound for generalization error in terms of mutual information which reveals an interesting interplay with known upper bounds that use the same quantity.

Learning with Differential Privacy: Stability, Learnability and the Sufficiency and Necessity of ERM Principle

While machine learning has proven to be a powerful data-driven solution to many real-life problems, its use in sensitive domains has been limited due to privacy concerns. A popular approach known as **differential privacy** offers provable privacy guarantees, but it is often observed in practice that it could substantially hamper learning accuracy. In this paper we study the learnability (whether a problem can be learned by any algorithm) under Vapnik's general learning setting with differential privacy constraint, and reveal some intricate relationships between privacy, stability and learnability. In particular, we show that a problem is privately learnable **if an only if** there is a private algorithm that asymptotically minimizes the empirical risk (AERM). In contrast, for non-private learning AERM alone is not sufficient for learnability. This result suggests that when searching for private learning algorithms, we can restrict the search to algorithms that are AERM. In light of this, we propose a conceptual procedure that always finds a universally consistent algorithm whenever the problem is learnable under privacy constraint. We also propose a generic and practical algorithm and show that under very general conditions it privately learns a wide class of learning problems. Lastly, we extend some of the results to the more practical $(\epsilon,\delta)$-differential privacy and establish the existence of a phase-transition on the class of problems that are approximately privately learnable with respect to how small $\delta$ needs to be.

A Minimax Theory for Adaptive Data Analysis

In adaptive data analysis, the user makes a sequence of queries on the data, where at each step the choice of query may depend on the results in previous steps. The releases are often randomized in order to reduce overfitting for such adaptively chosen queries. In this paper, we propose a minimax framework for adaptive data analysis. Assuming Gaussianity of queries, we establish the first sharp minimax lower bound on the squared error in the order of $O(\frac{\sqrt{k}\sigma^2}{n})$, where $k$ is the number of queries asked, and $\sigma^2/n$ is the ordinary signal-to-noise ratio for a single query. Our lower bound is based on the construction of an approximately least favorable adversary who picks a sequence of queries that are most likely to be affected by overfitting. This approximately least favorable adversary uses only one level of adaptivity, suggesting that the minimax risk for 1-step adaptivity with k-1 initial releases and that for $k$-step adaptivity are on the same order. The key technical component of the lower bound proof is a reduction to finding the convoluting distribution that optimally obfuscates the sign of a Gaussian signal. Our lower bound construction also reveals a transparent and elementary proof of the matching upper bound as an alternative approach to Russo and Zou (2015), who used information-theoretic tools to provide the same upper bound. We believe that the proposed framework opens up opportunities to obtain theoretical insights for many other settings of adaptive data analysis, which would extend the idea to more practical realms.

Privacy for Free: Posterior Sampling and Stochastic Gradient Monte Carlo

We consider the problem of Bayesian learning on sensitive datasets and present two simple but somewhat surprising results that connect Bayesian learning to "differential privacy:, a cryptographic approach to protect individual-level privacy while permiting database-level utility. Specifically, we show that that under standard assumptions, getting one single sample from a posterior distribution is differentially private "for free". We will see that estimator is statistically consistent, near optimal and computationally tractable whenever the Bayesian model of interest is consistent, optimal and tractable. Similarly but separately, we show that a recent line of works that use stochastic gradient for Hybrid Monte Carlo (HMC) sampling also preserve differentially privacy with minor or no modifications of the algorithmic procedure at all, these observations lead to an "anytime" algorithm for Bayesian learning under privacy constraint. We demonstrate that it performs much better than the state-of-the-art differential private methods on synthetic and real datasets.

Differentially-Private Logistic Regression for Detecting Multiple-SNP Association in GWAS Databases

Following the publication of an attack on genome-wide association studies (GWAS) data proposed by Homer et al., considerable attention has been given to developing methods for releasing GWAS data in a privacy-preserving way. Here, we develop an end-to-end differentially private method for solving regression problems with convex penalty functions and selecting the penalty parameters by cross-validation. In particular, we focus on penalized logistic regression with elastic-net regularization, a method widely used to in GWAS analyses to identify disease-causing genes. We show how a differentially private procedure for penalized logistic regression with elastic-net regularization can be applied to the analysis of GWAS data and evaluate our method's performance.

A Generalized Fellegi-Sunter Framework for Multiple Record Linkage With Application to Homicide Record Systems

We present a probabilistic method for linking multiple datafiles. This task is not trivial in the absence of unique identifiers for the individuals recorded. This is a common scenario when linking census data to coverage measurement surveys for census coverage evaluation, and in general when multiple record-systems need to be integrated for posterior analysis. Our method generalizes the Fellegi-Sunter theory for linking records from two datafiles and its modern implementations. The multiple record linkage goal is to classify the record K-tuples coming from K datafiles according to the different matching patterns. Our method incorporates the transitivity of agreement in the computation of the data used to model matching probabilities. We use a mixture model to fit matching probabilities via maximum likelihood using the EM algorithm. We present a method to decide the record K-tuples membership to the subsets of matching patterns and we prove its optimality. We apply our method to the integration of three Colombian homicide record systems and we perform a simulation study in order to explore the performance of the method under measurement error and different scenarios. The proposed method works well and opens some directions for future research.

On the Geometry of Discrete Exponential Families with Application to Exponential Random Graph Models

There has been an explosion of interest in statistical models for analyzing network data, and considerable interest in the class of exponential random graph (ERG) models, especially in connection with difficulties in computing maximum likelihood estimates. The issues associated with these difficulties relate to the broader structure of discrete exponential families. This paper re-examines the issues in two parts. First we consider the closure of $k$-dimensional exponential families of distribution with discrete base measure and polyhedral convex support $\mathrm{P}$. We show that the normal fan of $\mathrm{P}$ is a geometric object that plays a fundamental role in deriving the statistical and geometric properties of the corresponding extended exponential families. We discuss its relevance to maximum likelihood estimation, both from a theoretical and computational standpoint. Second, we apply our results to the analysis of ERG models. In particular, by means of a detailed example, we provide some characterization of the properties of ERG models, and, in particular, of certain behaviors of ERG models known as degeneracy.