Graph Neural Networks for Heart Failure Prediction on an EHR-Based Patient Similarity Graph

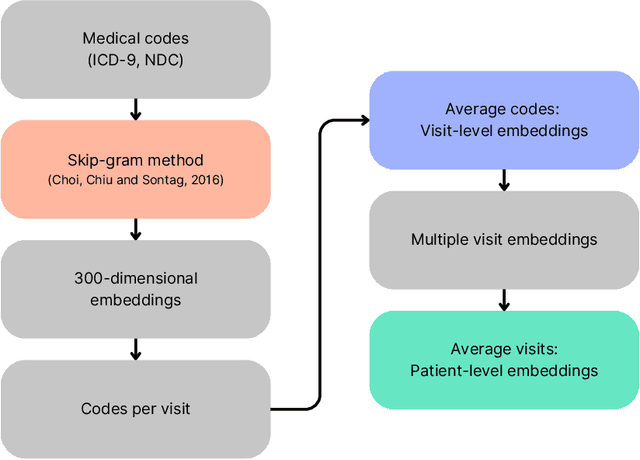
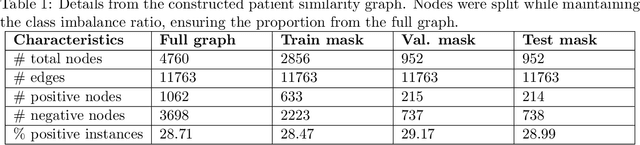
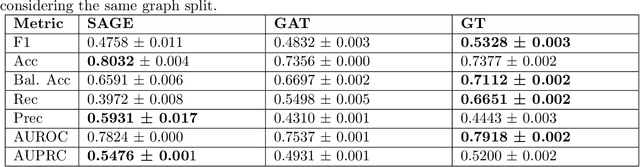
Objective: In modern healthcare, accurately predicting diseases is a crucial matter. This study introduces a novel approach using graph neural networks (GNNs) and a Graph Transformer (GT) to predict the incidence of heart failure (HF) on a patient similarity graph at the next hospital visit. Materials and Methods: We used electronic health records (EHR) from the MIMIC-III dataset and applied the K-Nearest Neighbors (KNN) algorithm to create a patient similarity graph using embeddings from diagnoses, procedures, and medications. Three models - GraphSAGE, Graph Attention Network (GAT), and Graph Transformer (GT) - were implemented to predict HF incidence. Model performance was evaluated using F1 score, AUROC, and AUPRC metrics, and results were compared against baseline algorithms. An interpretability analysis was performed to understand the model's decision-making process. Results: The GT model demonstrated the best performance (F1 score: 0.5361, AUROC: 0.7925, AUPRC: 0.5168). Although the Random Forest (RF) baseline achieved a similar AUPRC value, the GT model offered enhanced interpretability due to the use of patient relationships in the graph structure. A joint analysis of attention weights, graph connectivity, and clinical features provided insight into model predictions across different classification groups. Discussion and Conclusion: Graph-based approaches such as GNNs provide an effective framework for predicting HF. By leveraging a patient similarity graph, GNNs can capture complex relationships in EHR data, potentially improving prediction accuracy and clinical interpretability.

Latent Space Score-based Diffusion Model for Probabilistic Multivariate Time Series Imputation

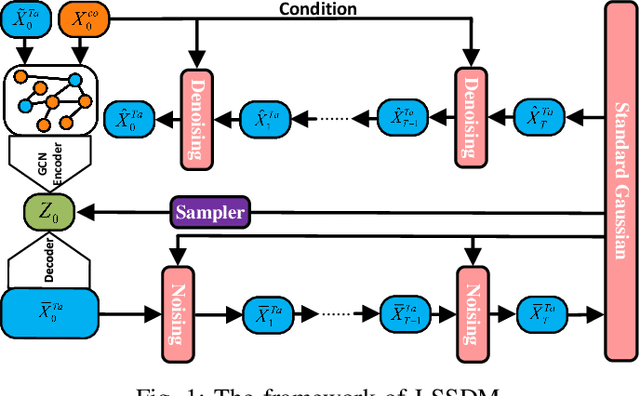
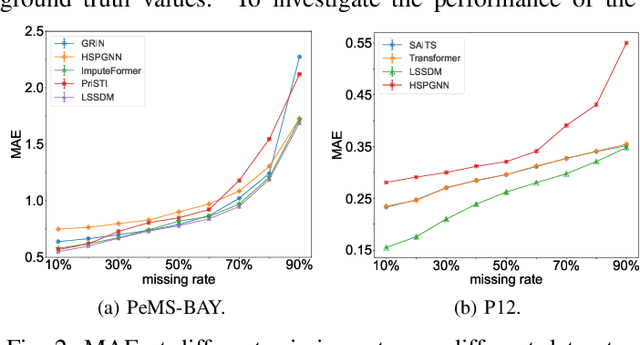
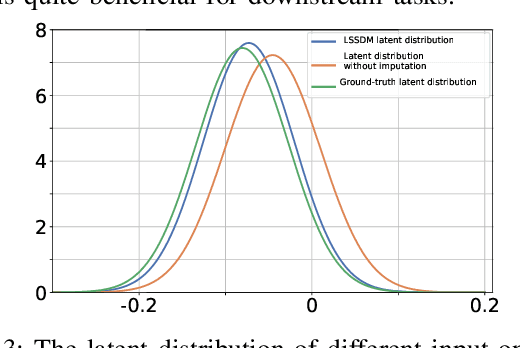
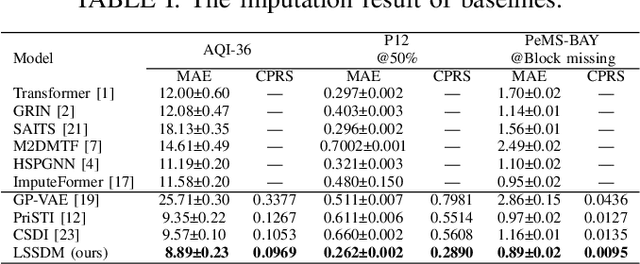
Accurate imputation is essential for the reliability and success of downstream tasks. Recently, diffusion models have attracted great attention in this field. However, these models neglect the latent distribution in a lower-dimensional space derived from the observed data, which limits the generative capacity of the diffusion model. Additionally, dealing with the original missing data without labels becomes particularly problematic. To address these issues, we propose the Latent Space Score-Based Diffusion Model (LSSDM) for probabilistic multivariate time series imputation. Observed values are projected onto low-dimensional latent space and coarse values of the missing data are reconstructed without knowing their ground truth values by this unsupervised learning approach. Finally, the reconstructed values are fed into a conditional diffusion model to obtain the precise imputed values of the time series. In this way, LSSDM not only possesses the power to identify the latent distribution but also seamlessly integrates the diffusion model to obtain the high-fidelity imputed values and assess the uncertainty of the dataset. Experimental results demonstrate that LSSDM achieves superior imputation performance while also providing a better explanation and uncertainty analysis of the imputation mechanism. The website of the code is \textit{https://github.com/gorgen2020/LSSDM\_imputation}.

Expected Grad-CAM: Towards gradient faithfulness

Although input-gradients techniques have evolved to mitigate and tackle the challenges associated with gradients, modern gradient-weighted CAM approaches still rely on vanilla gradients, which are inherently susceptible to the saturation phenomena. Despite recent enhancements have incorporated counterfactual gradient strategies as a mitigating measure, these local explanation techniques still exhibit a lack of sensitivity to their baseline parameter. Our work proposes a gradient-weighted CAM augmentation that tackles both the saturation and sensitivity problem by reshaping the gradient computation, incorporating two well-established and provably approaches: Expected Gradients and kernel smoothing. By revisiting the original formulation as the smoothed expectation of the perturbed integrated gradients, one can concurrently construct more faithful, localized and robust explanations which minimize infidelity. Through fine modulation of the perturbation distribution it is possible to regulate the complexity characteristic of the explanation, selectively discriminating stable features. Our technique, Expected Grad-CAM, differently from recent works, exclusively optimizes the gradient computation, purposefully designed as an enhanced substitute of the foundational Grad-CAM algorithm and any method built therefrom. Quantitative and qualitative evaluations have been conducted to assess the effectiveness of our method.

Physics-incorporated Graph Neural Network for Multivariate Time Series Imputation

Exploring the missing values is an essential but challenging issue due to the complex latent spatio-temporal correlation and dynamic nature of time series. Owing to the outstanding performance in dealing with structure learning potentials, Graph Neural Networks (GNNs) and Recurrent Neural Networks (RNNs) are often used to capture such complex spatio-temporal features in multivariate time series. However, these data-driven models often fail to capture the essential spatio-temporal relationships when significant signal corruption occurs. Additionally, calculating the high-order neighbor nodes in these models is of high computational complexity. To address these problems, we propose a novel higher-order spatio-temporal physics-incorporated GNN (HSPGNN). Firstly, the dynamic Laplacian matrix can be obtained by the spatial attention mechanism. Then, the generic inhomogeneous partial differential equation (PDE) of physical dynamic systems is used to construct the dynamic higher-order spatio-temporal GNN to obtain the missing time series values. Moreover, we estimate the missing impact by Normalizing Flows (NF) to evaluate the importance of each node in the graph for better explainability. Experimental results on four benchmark datasets demonstrate the effectiveness of HSPGNN and the superior performance when combining various order neighbor nodes. Also, graph-like optical flow, dynamic graphs, and missing impact can be obtained naturally by HSPGNN, which provides better dynamic analysis and explanation than traditional data-driven models. Our code is available at https://github.com/gorgen2020/HSPGNN.

Dynamic Causal Explanation Based Diffusion-Variational Graph Neural Network for Spatio-temporal Forecasting

Graph neural networks (GNNs), especially dynamic GNNs, have become a research hotspot in spatio-temporal forecasting problems. While many dynamic graph construction methods have been developed, relatively few of them explore the causal relationship between neighbour nodes. Thus, the resulting models lack strong explainability for the causal relationship between the neighbour nodes of the dynamically generated graphs, which can easily lead to a risk in subsequent decisions. Moreover, few of them consider the uncertainty and noise of dynamic graphs based on the time series datasets, which are ubiquitous in real-world graph structure networks. In this paper, we propose a novel Dynamic Diffusion-Variational Graph Neural Network (DVGNN) for spatio-temporal forecasting. For dynamic graph construction, an unsupervised generative model is devised. Two layers of graph convolutional network (GCN) are applied to calculate the posterior distribution of the latent node embeddings in the encoder stage. Then, a diffusion model is used to infer the dynamic link probability and reconstruct causal graphs in the decoder stage adaptively. The new loss function is derived theoretically, and the reparameterization trick is adopted in estimating the probability distribution of the dynamic graphs by Evidence Lower Bound during the backpropagation period. After obtaining the generated graphs, dynamic GCN and temporal attention are applied to predict future states. Experiments are conducted on four real-world datasets of different graph structures in different domains. The results demonstrate that the proposed DVGNN model outperforms state-of-the-art approaches and achieves outstanding Root Mean Squared Error result while exhibiting higher robustness. Also, by F1-score and probability distribution analysis, we demonstrate that DVGNN better reflects the causal relationship and uncertainty of dynamic graphs.