Latent Space Score-based Diffusion Model for Probabilistic Multivariate Time Series Imputation

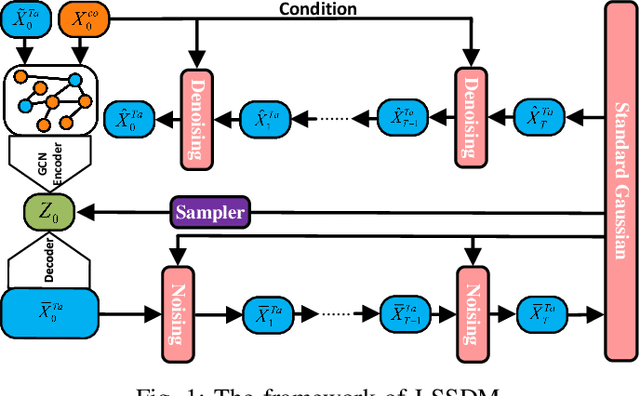
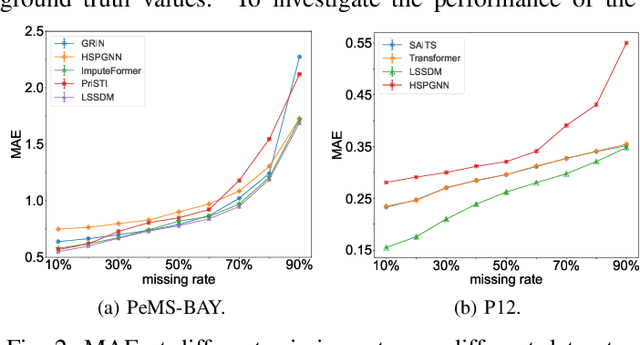
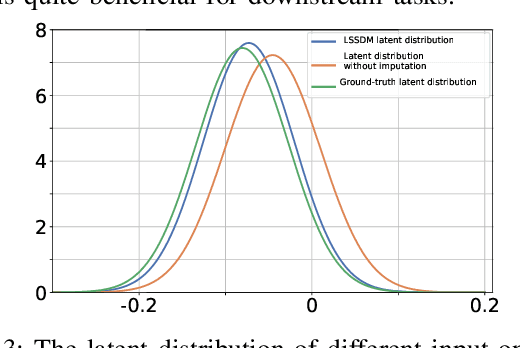
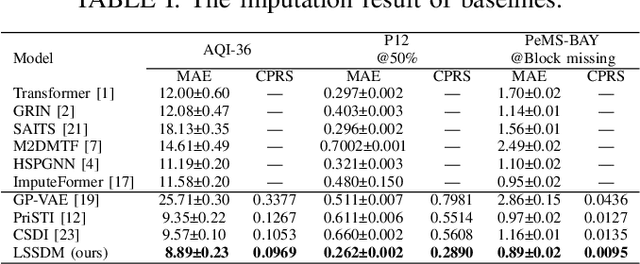
Accurate imputation is essential for the reliability and success of downstream tasks. Recently, diffusion models have attracted great attention in this field. However, these models neglect the latent distribution in a lower-dimensional space derived from the observed data, which limits the generative capacity of the diffusion model. Additionally, dealing with the original missing data without labels becomes particularly problematic. To address these issues, we propose the Latent Space Score-Based Diffusion Model (LSSDM) for probabilistic multivariate time series imputation. Observed values are projected onto low-dimensional latent space and coarse values of the missing data are reconstructed without knowing their ground truth values by this unsupervised learning approach. Finally, the reconstructed values are fed into a conditional diffusion model to obtain the precise imputed values of the time series. In this way, LSSDM not only possesses the power to identify the latent distribution but also seamlessly integrates the diffusion model to obtain the high-fidelity imputed values and assess the uncertainty of the dataset. Experimental results demonstrate that LSSDM achieves superior imputation performance while also providing a better explanation and uncertainty analysis of the imputation mechanism. The website of the code is \textit{https://github.com/gorgen2020/LSSDM\_imputation}.

Establishing strong imputation performance of a denoising autoencoder in a wide range of missing data problems

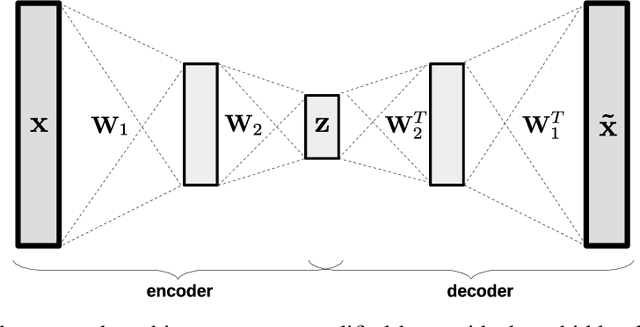
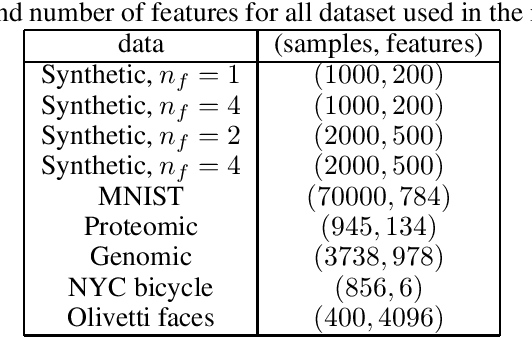
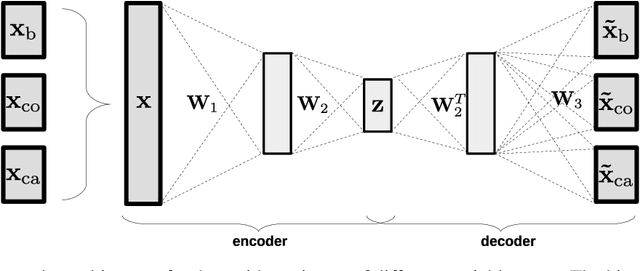
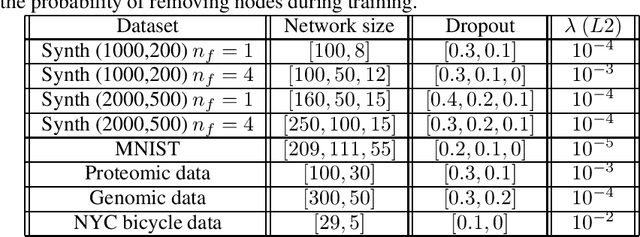
Dealing with missing data in data analysis is inevitable. Although powerful imputation methods that address this problem exist, there is still much room for improvement. In this study, we examined single imputation based on deep autoencoders, motivated by the apparent success of deep learning to efficiently extract useful dataset features. We have developed a consistent framework for both training and imputation. Moreover, we benchmarked the results against state-of-the-art imputation methods on different data sizes and characteristics. The work was not limited to the one-type variable dataset; we also imputed missing data with multi-type variables, e.g., a combination of binary, categorical, and continuous attributes. To evaluate the imputation methods, we randomly corrupted the complete data, with varying degrees of corruption, and then compared the imputed and original values. In all experiments, the developed autoencoder obtained the smallest error for all ranges of initial data corruption.

Variational auto-encoders with Student's t-prior

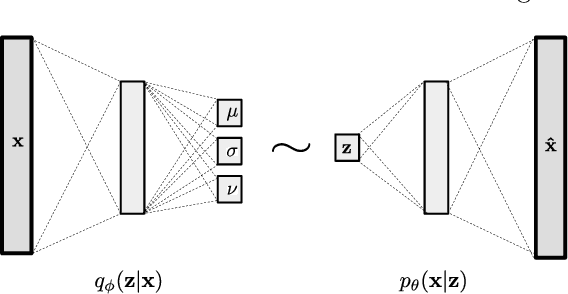
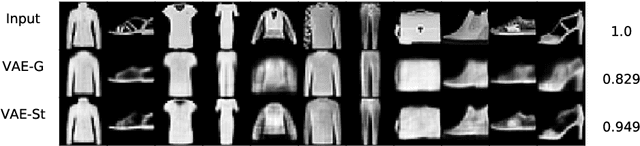
We propose a new structure for the variational auto-encoders (VAEs) prior, with the weakly informative multivariate Student's t-distribution. In the proposed model all distribution parameters are trained, thereby allowing for a more robust approximation of the underlying data distribution. We used Fashion-MNIST data in two experiments to compare the proposed VAEs with the standard Gaussian priors. Both experiments showed a better reconstruction of the images with VAEs using Student's t-prior distribution.