FastCHGNet: Training one Universal Interatomic Potential to 1.5 Hours with 32 GPUs

Graph neural network universal interatomic potentials (GNN-UIPs) have demonstrated remarkable generalization and transfer capabilities in material discovery and property prediction. These models can accelerate molecular dynamics (MD) simulation by several orders of magnitude while maintaining \textit{ab initio} accuracy, making them a promising new paradigm in material simulations. One notable example is Crystal Hamiltonian Graph Neural Network (CHGNet), pretrained on the energies, forces, stresses, and magnetic moments from the MPtrj dataset, representing a state-of-the-art GNN-UIP model for charge-informed MD simulations. However, training the CHGNet model is time-consuming(8.3 days on one A100 GPU) for three reasons: (i) requiring multi-layer propagation to reach more distant atom information, (ii) requiring second-order derivatives calculation to finish weights updating and (iii) the implementation of reference CHGNet does not fully leverage the computational capabilities. This paper introduces FastCHGNet, an optimized CHGNet, with three contributions: Firstly, we design innovative Force/Stress Readout modules to decompose Force/Stress prediction. Secondly, we adopt massive optimizations such as kernel fusion, redundancy bypass, etc, to exploit GPU computation power sufficiently. Finally, we extend CHGNet to support multiple GPUs and propose a load-balancing technique to enhance GPU utilization. Numerical results show that FastCHGNet reduces memory footprint by a factor of 3.59. The final training time of FastCHGNet can be decreased to \textbf{1.53 hours} on 32 GPUs without sacrificing model accuracy.

Compositionally Generalizable 3D Structure Prediction

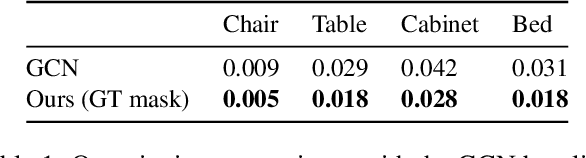
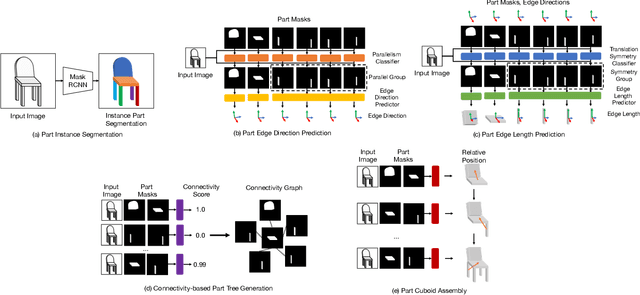
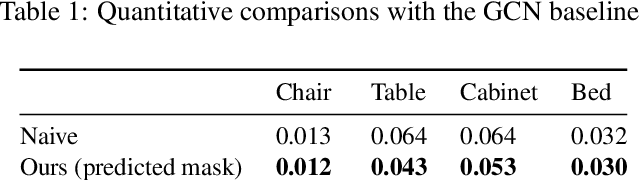
Single-image 3D shape reconstruction is an important and long-standing problem in computer vision. A plethora of existing works is constantly pushing the state-of-the-art performance in the deep learning era. However, there remains a much difficult and largely under-explored issue on how to generalize the learned skills over novel unseen object categories that have very different shape geometry distribution. In this paper, we bring in the concept of compositional generalizability and propose a novel framework that factorizes the 3D shape reconstruction problem into proper sub-problems, each of which is tackled by a carefully designed neural sub-module with generalizability guarantee. The intuition behind our formulation is that object parts (slates and cylindrical parts), their relationships (adjacency, equal-length, and parallelism) and shape substructures (T-junctions and a symmetric group of parts) are mostly shared across object categories, even though the object geometry may look very different (chairs and cabinets). Experiments on PartNet show that we achieve superior performance than baseline methods, which validates our problem factorization and network designs.

Learning to Group: A Bottom-Up Framework for 3D Part Discovery in Unseen Categories

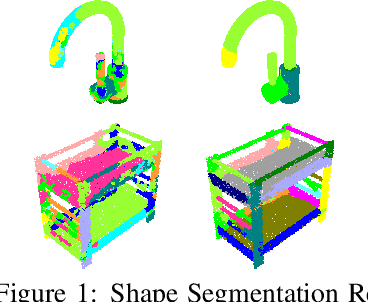
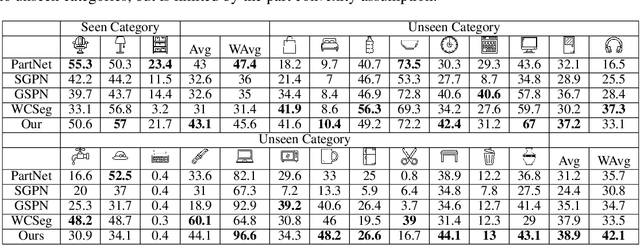
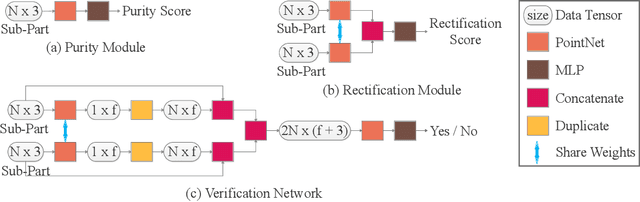
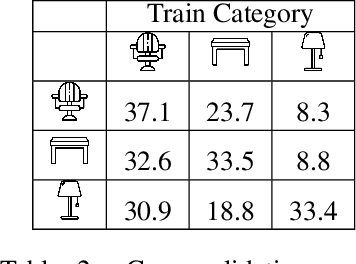
We address the problem of discovering 3D parts for objects in unseen categories. Being able to learn the geometry prior of parts and transfer this prior to unseen categories pose fundamental challenges on data-driven shape segmentation approaches. Formulated as a contextual bandit problem, we propose a learning-based agglomerative clustering framework which learns a grouping policy to progressively group small part proposals into bigger ones in a bottom-up fashion. At the core of our approach is to restrict the local context for extracting part-level features, which encourages the generalizability to unseen categories. On the large-scale fine-grained 3D part dataset, PartNet, we demonstrate that our method can transfer knowledge of parts learned from 3 training categories to 21 unseen testing categories without seeing any annotated samples. Quantitative comparisons against four shape segmentation baselines shows that our approach achieve the state-of-the-art performance.