MatRIS: Toward Reliable and Efficient Pretrained Machine Learning Interatomic Potentials

Foundation MLIPs demonstrate broad applicability across diverse material systems and have emerged as a powerful and transformative paradigm in chemical and computational materials science. Equivariant MLIPs achieve state-of-the-art accuracy in a wide range of benchmarks by incorporating equivariant inductive bias. However, the reliance on tensor products and high-degree representations makes them computationally costly. This raises a fundamental question: as quantum mechanical-based datasets continue to expand, can we develop a more compact model to thoroughly exploit high-dimensional atomic interactions? In this work, we present MatRIS (\textbf{Mat}erials \textbf{R}epresentation and \textbf{I}nteraction \textbf{S}imulation), an invariant MLIP that introduces attention-based modeling of three-body interactions. MatRIS leverages a novel separable attention mechanism with linear complexity $O(N)$, enabling both scalability and expressiveness. MatRIS delivers accuracy comparable to that of leading equivariant models on a wide range of popular benchmarks (Matbench-Discovery, MatPES, MDR phonon, Molecular dataset, etc). Taking Matbench-Discovery as an example, MatRIS achieves an F1 score of up to 0.847 and attains comparable accuracy at a lower training cost. The work indicates that our carefully designed invariant models can match or exceed the accuracy of equivariant models at a fraction of the cost, shedding light on the development of accurate and efficient MLIPs.

Exploring Landscapes for Better Minima along Valleys

Finding lower and better-generalizing minima is crucial for deep learning. However, most existing optimizers stop searching the parameter space once they reach a local minimum. Given the complex geometric properties of the loss landscape, it is difficult to guarantee that such a point is the lowest or provides the best generalization. To address this, we propose an adaptor "E" for gradient-based optimizers. The adapted optimizer tends to continue exploring along landscape valleys (areas with low and nearly identical losses) in order to search for potentially better local minima even after reaching a local minimum. This approach increases the likelihood of finding a lower and flatter local minimum, which is often associated with better generalization. We also provide a proof of convergence for the adapted optimizers in both convex and non-convex scenarios for completeness. Finally, we demonstrate their effectiveness in an important but notoriously difficult training scenario, large-batch training, where Lamb is the benchmark optimizer. Our testing results show that the adapted Lamb, ALTO, increases the test accuracy (generalization) of the current state-of-the-art optimizer by an average of 2.5% across a variety of large-batch training tasks. This work potentially opens a new research direction in the design of optimization algorithms.

Skrull: Towards Efficient Long Context Fine-tuning through Dynamic Data Scheduling

Long-context supervised fine-tuning (Long-SFT) plays a vital role in enhancing the performance of large language models (LLMs) on long-context tasks. To smoothly adapt LLMs to long-context scenarios, this process typically entails training on mixed datasets containing both long and short sequences. However, this heterogeneous sequence length distribution poses significant challenges for existing training systems, as they fail to simultaneously achieve high training efficiency for both long and short sequences, resulting in sub-optimal end-to-end system performance in Long-SFT. In this paper, we present a novel perspective on data scheduling to address the challenges posed by the heterogeneous data distributions in Long-SFT. We propose Skrull, a dynamic data scheduler specifically designed for efficient long-SFT. Through dynamic data scheduling, Skrull balances the computation requirements of long and short sequences, improving overall training efficiency. Furthermore, we formulate the scheduling process as a joint optimization problem and thoroughly analyze the trade-offs involved. Based on those analysis, Skrull employs a lightweight scheduling algorithm to achieve near-zero cost online scheduling in Long-SFT. Finally, we implement Skrull upon DeepSpeed, a state-of-the-art distributed training system for LLMs. Experimental results demonstrate that Skrull outperforms DeepSpeed by 3.76x on average (up to 7.54x) in real-world long-SFT scenarios.

FastCHGNet: Training one Universal Interatomic Potential to 1.5 Hours with 32 GPUs

Graph neural network universal interatomic potentials (GNN-UIPs) have demonstrated remarkable generalization and transfer capabilities in material discovery and property prediction. These models can accelerate molecular dynamics (MD) simulation by several orders of magnitude while maintaining \textit{ab initio} accuracy, making them a promising new paradigm in material simulations. One notable example is Crystal Hamiltonian Graph Neural Network (CHGNet), pretrained on the energies, forces, stresses, and magnetic moments from the MPtrj dataset, representing a state-of-the-art GNN-UIP model for charge-informed MD simulations. However, training the CHGNet model is time-consuming(8.3 days on one A100 GPU) for three reasons: (i) requiring multi-layer propagation to reach more distant atom information, (ii) requiring second-order derivatives calculation to finish weights updating and (iii) the implementation of reference CHGNet does not fully leverage the computational capabilities. This paper introduces FastCHGNet, an optimized CHGNet, with three contributions: Firstly, we design innovative Force/Stress Readout modules to decompose Force/Stress prediction. Secondly, we adopt massive optimizations such as kernel fusion, redundancy bypass, etc, to exploit GPU computation power sufficiently. Finally, we extend CHGNet to support multiple GPUs and propose a load-balancing technique to enhance GPU utilization. Numerical results show that FastCHGNet reduces memory footprint by a factor of 3.59. The final training time of FastCHGNet can be decreased to \textbf{1.53 hours} on 32 GPUs without sacrificing model accuracy.

Deep Density: circumventing the Kohn-Sham equations via symmetry preserving neural networks

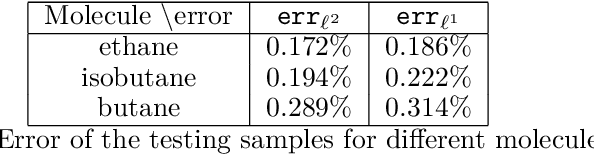
The recently developed Deep Potential [Phys. Rev. Lett. 120, 143001, 2018] is a powerful method to represent general inter-atomic potentials using deep neural networks. The success of Deep Potential rests on the proper treatment of locality and symmetry properties of each component of the network. In this paper, we leverage its network structure to effectively represent the mapping from the atomic configuration to the electron density in Kohn-Sham density function theory (KS-DFT). By directly targeting at the self-consistent electron density, we demonstrate that the adapted network architecture, called the Deep Density, can effectively represent the electron density as the linear combination of contributions from many local clusters. The network is constructed to satisfy the translation, rotation, and permutation symmetries, and is designed to be transferable to different system sizes. We demonstrate that using a relatively small number of training snapshots, Deep Density achieves excellent performance for one-dimensional insulating and metallic systems, as well as systems with mixed insulating and metallic characters. We also demonstrate its performance for real three-dimensional systems, including small organic molecules, as well as extended systems such as water (up to $512$ molecules) and aluminum (up to $256$ atoms).