Stochastic Poisson Surface Reconstruction with One Solve using Geometric Gaussian Processes

Poisson Surface Reconstruction is a widely-used algorithm for reconstructing a surface from an oriented point cloud. To facilitate applications where only partial surface information is available, or scanning is performed sequentially, a recent line of work proposes to incorporate uncertainty into the reconstructed surface via Gaussian process models. The resulting algorithms first perform Gaussian process interpolation, then solve a set of volumetric partial differential equations globally in space, resulting in a computationally expensive two-stage procedure. In this work, we apply recently-developed techniques from geometric Gaussian processes to combine interpolation and surface reconstruction into a single stage, requiring only one linear solve per sample. The resulting reconstructed surface samples can be queried locally in space, without the use of problem-dependent volumetric meshes or grids. These capabilities enable one to (a) perform probabilistic collision detection locally around the region of interest, (b) perform ray casting without evaluating points not on the ray's trajectory, and (c) perform next-view planning on a per-slice basis. They also improve reconstruction quality, by not requiring one to approximate kernel matrix inverses with diagonal matrices as part of intermediate computations. Results show that our approach provides a cleaner, more-principled, and more-flexible stochastic surface reconstruction pipeline.

Through the Looking Glass: Mirror Schrödinger Bridges

Resampling from a target measure whose density is unknown is a fundamental problem in mathematical statistics and machine learning. A setting that dominates the machine learning literature consists of learning a map from an easy-to-sample prior, such as the Gaussian distribution, to a target measure. Under this model, samples from the prior are pushed forward to generate a new sample on the target measure, which is often difficult to sample from directly. In this paper, we propose a new model for conditional resampling called mirror Schr\"odinger bridges. Our key observation is that solving the Schr\"odinger bridge problem between a distribution and itself provides a natural way to produce new samples from conditional distributions, giving in-distribution variations of an input data point. We show how to efficiently solve this largely overlooked version of the Schr\"odinger bridge problem. We prove that our proposed method leads to significant algorithmic simplifications over existing alternatives, in addition to providing control over in-distribution variation. Empirically, we demonstrate how these benefits can be leveraged to produce proximal samples in a number of application domains.

Neural Stochastic Screened Poisson Reconstruction

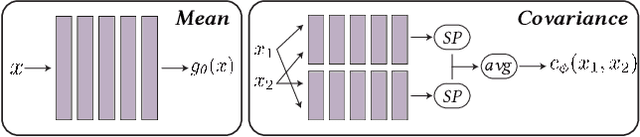
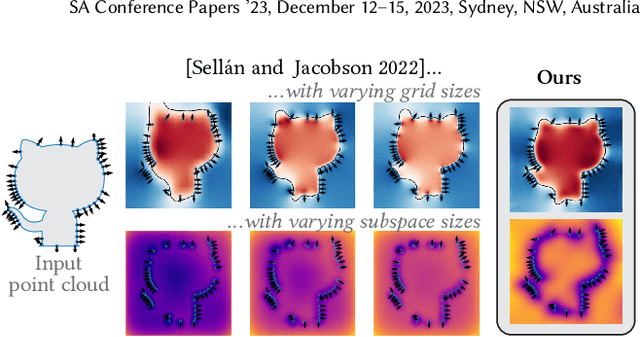
Reconstructing a surface from a point cloud is an underdetermined problem. We use a neural network to study and quantify this reconstruction uncertainty under a Poisson smoothness prior. Our algorithm addresses the main limitations of existing work and can be fully integrated into the 3D scanning pipeline, from obtaining an initial reconstruction to deciding on the next best sensor position and updating the reconstruction upon capturing more data.

Bayes' Rays: Uncertainty Quantification for Neural Radiance Fields

Neural Radiance Fields (NeRFs) have shown promise in applications like view synthesis and depth estimation, but learning from multiview images faces inherent uncertainties. Current methods to quantify them are either heuristic or computationally demanding. We introduce BayesRays, a post-hoc framework to evaluate uncertainty in any pre-trained NeRF without modifying the training process. Our method establishes a volumetric uncertainty field using spatial perturbations and a Bayesian Laplace approximation. We derive our algorithm statistically and show its superior performance in key metrics and applications. Additional results available at: https://bayesrays.github.io.

Breaking Bad: A Dataset for Geometric Fracture and Reassembly

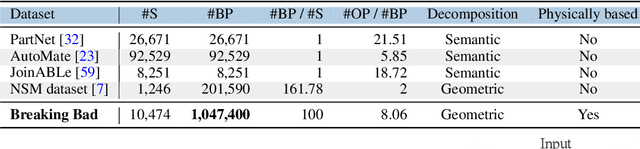
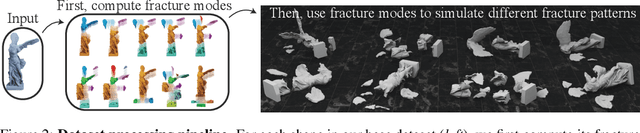
We introduce Breaking Bad, a large-scale dataset of fractured objects. Our dataset consists of over one million fractured objects simulated from ten thousand base models. The fracture simulation is powered by a recent physically based algorithm that efficiently generates a variety of fracture modes of an object. Existing shape assembly datasets decompose objects according to semantically meaningful parts, effectively modeling the construction process. In contrast, Breaking Bad models the destruction process of how a geometric object naturally breaks into fragments. Our dataset serves as a benchmark that enables the study of fractured object reassembly and presents new challenges for geometric shape understanding. We analyze our dataset with several geometry measurements and benchmark three state-of-the-art shape assembly deep learning methods under various settings. Extensive experimental results demonstrate the difficulty of our dataset, calling on future research in model designs specifically for the geometric shape assembly task. We host our dataset at https://breaking-bad-dataset.github.io/.